Ikki noma`lumli tenglamalar Reja:

1. Ikki noma`lumli tenglamaning geometrik ma`nosi

2. Tenglamalar sistemasining geometrik ma`nosi

3. Tenglamalar sistemasini yechishning turli usullari

4. Ikkinchi va uchinchi tartibli determinantlar

5. Chiziqli tenglamalar sistemasini Kramer usulida yechish

6. Tengsizliklar sistemasini yechish

7. Modul qatnashgan tenglama va tengsizliklar

8. Matnli masalalarni yechish

Ikki noma`lumli tenglamaning geometrik ma`nosi

Umumiy qilib aytganda, har qanday ikki x va y noma`lum ga bog`-liq bo`lgan tenglama tekislikda shunday nuqtalarning geometrik o`rnini bildiradiki, bu nuqtalarning koordinatalari shu tenglamani qanoatlantiradi. x va y ga bog`liq bo`lgan tenglamani

F(x,y)=0 (1)

ko`rinishida yozish mumkin. Bu tenglama qanday bo`lganda, qanday chiziq aniqlanishini misollarda ko`rib chiqamiz.

1. (1) tenglama Ax+By+C=0 ko`rinishidagi chiziqli tenglama bo`l-sin. Bu holda o`zgaruvchi x ning har bir qiymatiga y ning bitta qiymati mos keladi. Bunday (x,y) juftlardan bir nechtasini topib tekislikda belgi-laymiz va ularni tutashtirib, to`g`ri chiziqni hosil qilamiz.

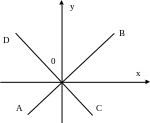
Misol. 1) y=x tenglama birinchi va uchinchi koordinatalar burcha-gining bissektrisasini bildiradi (AB to`g`ri chiziq).

2. y=-x tenglama esa ikkinchi va to`rtinchi koordinatalar burchagi-ning bissektrisasini aniqlaydi (CD to`g`ri chiziq) (6-rasm).

-2

6-rasm. 7-rasm.

Tenglamada o`zgaruvchilardan faqat bittasi qatnashishi mumkin. Bu holda ham tenglama biror chiziqni bildiradi.

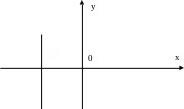
Misol. x+2=0 tenglama berilgan bo`lsin.

Bundan x=-2 ni topamiz. Bu tenglama shunday nuqtalarning geometrik o`rnini aniqlaydiki, ularning har birining abssissasi x=-2 bo`lib, ordinatasi ixtiyoriy bo`ladi, bunday nuqtalar abssissa o`qidan – 2 ga teng nuqtadan o`tadi va 0y o`qiga parallel bo`lgan to`g`ri chiziq bo`ladi (7-rasm).

Shunga o`xshash, y – 3=0 tenglama ordinata o`qidan 3 ga teng kes-mani ajratuvchi va 0x o`qiga parallel bo`lgan to`g`ri chiziqni bildiradi (8-rasm).

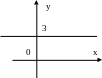
y

4

8-rasm. 9-rasm.

2. Ikkinchi darajali noma`lum qatnashgan tenglamani ko`rib chiqamiz.

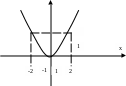
Misol. 1) x²-y=0 tenglama uchi koordinatalar boshida va tarmoqlari yuqoriga qaragan parabolani bildiradi (9-rasm).

2) x²+y²=4 tenglama markazi koordinatalar boshida, radiusi R=2 bo`lgan aylanani bildiradi (10-rasm).

10-rasm.

3. Agar (1) tenglamaning chap tomoni ko`paytuvchilarga ajralsa, har bir ko`paytuvchini alohida-alohida nolga tenglashtirib, bir nechta chiziqlarni hosil qilamiz.

Misol. x²-y²=0 yoki (x+y) (x-y)=0 tenglama x+y=0 va x-y=0 to`g`ri chiziqlar juftini aniqlaydi.

1. Xususiy holda F(x,y)=0 tenglama bitta yoki bir nechta nuqtalar-dan iborat bo`lgan to`plamni aniqlashi mumkin.

Misol. x²+y²=0 tenglama faqat O(0,0) nuqtani ifodalaydi (x²-4)²+(y²-1)²=0 tenglama to`rtta nuqta (-2;-1), (-2;1), (2;-1), (2;1) ni aniq-laydi.

5. F(x,y)=0 tenglama bironta ham nuqtani aniqlamasligi mumkin. Misol, x²+y²+1=0 tenglamani haqiqiy sonlar juftining birontasi ham qanoat-lantirmaydi, demak bu tenglamaga hech qanday nuqta mos kelmaydi.