30

СУМСЬКЕ ТЕРИТОРІАЛЬНЕ ВІДДІЛЕННЯ

МАЛОЇ АКАДЕМІЇ НАУК УКРАЇНИ

ШОСТКИНСЬКА СТАНЦІЯ ЮНИХ ТЕХНІКІВ ШОСТКИНСЬКОЇ МІСЬКОЇ РАДИ

шосткинська спеціалізована школа І-ІІІ ступенів №1

СЕКЦІЯ прикладна МАТЕМАТИКа

МАТЕМАТИКА ТА ШАХИ

Роботу виконав

Дель Максим Віталійович,

учень 11-А класу

Шосткинської спеціалізованої школи І-ІІІ ступенів №1,

вихованець гуртка "Рішення шахових дебютів" станції юних техніків Шосткинської міської ради Сумської області

Наукові керівники:

Кочубей Світлана Григорівна,

керівник гуртка станції юних техніків Шосткинської міської ради Сумської області,

Галібаренко Людмила Акимівна,

вчитель математики ШСШ №1

Шостка 2011

ЗМІСТ

ВСТУП…………………………………………………………………......…. 3

ОСНОВНА ЧАСТИНА

РОЗДІЛ 1. ТЕОРЕТИЧНА ЧАСТИНА……………………………...………... 5

1.1. Виникнення шахів……………………......................................... 4

1.2. Геометрія в процесі гри…………..…………………................. 5

1.2.1. Шахова гра, як математичне креслення ………….…… 8

1.2.2. Правило квадрата.....…..………………………………… 10

1.2.3. Правило трикутника …..………………………………… 11

1.2.4. Відстань між двома точками на шахівниці …………......... 4

1.2.5 . Симетрія в шахах ……........................................................... 4

РОЗДІЛ 2. КЛАСИФІКАЦІЯ, АНАЛІЗ ТА РОЗВ’ЯЗАННЯ

ШАХОВО-МАТЕМАТИЧНИХ ЗАДАЧ………………………………….. 5

2.1. Математика шахової дошки…………………...………………… 11

2.1.1. Задачі на розріз шахової дошки…………………..……… 8

2.1.2. Задачі на розфарбовування шахової дошки...…………... 10

2.1.3. Задачі на шахівницю та доміно ………….………………. 11

2.1.3. Алгебраїчні мотиви на шахівниці………….……………. 11

2.2. Математика шахових фігур …………………………………. 11

2.2.1. Задачі на парність і непарність…….………………....… 10

2.2.2. Здачі на знаходження числа фігур на шахівниці……….. 11

2.2.3. Задачі на знаходження числа ходів і шляхів

пересування шахових фігур……………………………... 14

2.2.4. Задачі на знаходження маршрутів фігур……………… 11

ВИСНОВКИ……………………………………………………………........ 18

ЛІТЕРАТУРА………………………………………………..………….......... 19

ВСТУП

Шахи - наука, і передусім - математика. Шахи вимагають колосальної людської думки, глибокий і великий розрахунок варіантів.

Вибір успішного рішення в складних ситуаціях, що виникають на практиці, можна порівняти з вибором хорошого ходу в шаховій партії в умовах обмеженого годині. Гра в шахи - не лише цікаве, але і корисне зайняття. Шахи розвивають творчі навички і комбінаторні здібності. Шахи – це і вид інтелектуальної боротьби, і змагання, а будь-яке змагання удосконалює сильні риси особистості. Проте будучи прекрасним відпочинком для юриста, лікаря, художника і навіть інженера, шахи ніяк не стають засобом розумової розрядки для математика, мозок якого при рішенні шахових проблем продовжує діяти в колишньому ключі.

Форми мислення математика і шахіста досить близькі, а математичні здібності нерідко поєднуються з шаховими. Шахами цікавилися такі учені, як Ломоносов, Менделєєв, Ньютон, Лейбніц, Бунаев, Пумнкаре, Паули, Гаус. Але в той же час, розуміючи величезне значення математики для розвитку інтелекту, також і багато великих шахістів захоплювалися рішенням математичних завдань і головоломок. Як приклад можна привести таких майстрів шахової гри як Еммануїл Ласкер, Михайло Ботвинник, Макс Эйве тощо. До речі, Эйве сказав, що "в математиці не менше логіки і краси, ніж в шахах".

Шахи справедливо вважають єдиною грою з усіх, придуманих людиною, в якій поєднуються спорт, мистецтво і наука.

Одночасно цікавлячись математикою і грою в шахи, я вирішив простежити як математичні знання використовуються на шаховій дошці, та як шахи допомагають у вирішенні математичних задач.

Майже в кожній збірці олімпіадних математичних завдань, або книзі головоломок і математичного дозвілля можна знайти красиві і дотепні завдання за участю шахівниці і фігур. Наприклад, завдання про хід коня, якою займався великий математик Леонард Ейлер, або завдання про вісім ферзів, їй займався великий математик Карл Гаусс.

Мета роботи :

1. Дослідити зв'язок математики і шахів

2. Встановити, яку роль відіграють шахи у справі математика та математика у справі шахіста.

Завдання:

1. Дослідити роль математики в історії виникнення шахів.

2. Встановити як проявляється математика у процесі шахової гри, які математичні «хитрощі» допомагають шахістам раціональніше вести партію.

3. Зібрати і розв’язати математичні задачі на шахову тематику.

4. Класифікувати шахово-математичні задачі.

Методи дослідження :

1. Розглядання безпосередньо процесу гри, на основі власного досвіду.

2. Аналіз і опрацювання літератури з питання шахів і математики.

3. Самостійне розв’язання, аналіз і класифікація задач.

• Усі представлені в роботі задачі мною рзв’язані. Умови задач узяті зі збірок олімпіадних математичних завдань, книг Е. Я. Гіка «Математика на шаховій дошці», Екимовой Н.А., Кукина Г.П. «Задачі на розрізання». а також використані матеріали шахового гуртка «Стратег». Особливістю моєї роботи є те, що я не просто проаналізував, розв’язав і зібрав максимальну кількість задач, що стосуються безпосередньо шахівниці і фігур, а й зробив максимально повну і детальну, класифікацію цих задач.

Практичне значення роботи полягає в тому, що завдання із застосуванням шахової теорії часто зустрічаються на олімпіадах по математиці, а також знання деяких, знайдених мною, математичних «хитрощів», допоможе шахістам раціональніше вести партію. В цьому і полягає актуальність обраної теми.

РОЗДІЛ 1. ТЕОРЕТИЧНА ЧАСТИНА

(Додаток А.)

1. Розділ 2. Класифікація, аналіз та розв’язання шахово- математичних задач

1. Математика шахівниці

   1. Задачі на розріз шахової дошки

Задача 1. Дано дві шахівниці: звичайна, в 64 клітини, і інша — в 36 клітин. Вимагається кожну з них розрізати на дві частини так, щоб з усіх отриманих чотирьох частин скласти нову шахівницю 10 × 10 клітин.

Розв'язання.

Р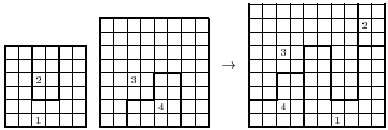 ис. 2.1

Відповідь: рис.

З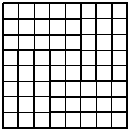 адача 2. Яке найбільше число смужок розмірами 1×5 полів можна викроїти з шахівниці?

Розв'язання. Зрозуміло, що більше 12 таких смужок викроїти не можна, а як викроїти 12 — видно з рисунка 2.2.

Відповідь: 12.

Рис. 2.2

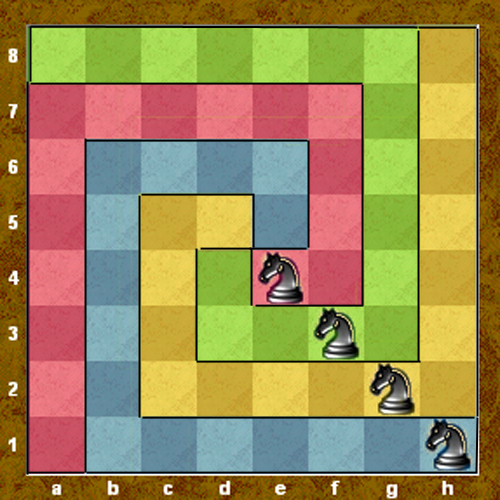
Задача 3. Розрізати дошку на чотири однакові частини(співпадаючі при накладенні) так, щоб на кожній з них виявилося по одному коню. Передбачається, що розрізи проходять тільки по межах між вертикалями і горизонталями дошки.

Розв'язання. Одне з рішень задачі представлене на рис.

Рис. 2.3

Розташовуючи чотирьох коней на різних полях дошки, можна отримати безліч завдань про розрізання. Інтерес в них представляє не лише знаходження одного необхідного розрізу, але і підрахунок числа усіх способів розрізати дошку на чотири однакові частини, що містять по одному коню.

Встановлено, що найбільше число рішень (800) завдання має при розташуванні коней в кутах дошки.

Відповідь: рис. 2.3.

З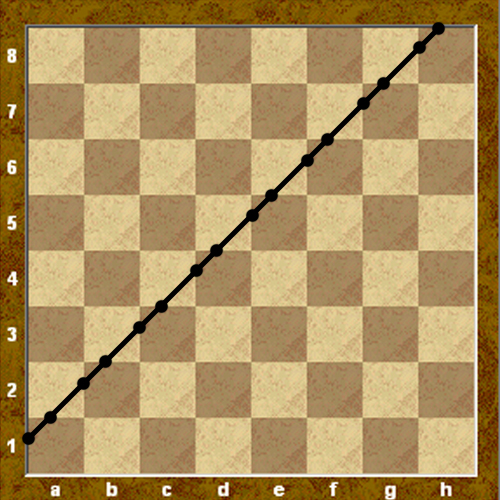 адача 4. Яке максимальне число полів дошки можна перетнути одним розрізом?

Розв'язання. Поля дошки утворюються в результаті перетину 18 прямих - дев'яти вертикальних і дев'яти горизонтальних.

З

Рис. 2.4

кожною з них пряма-розріз може перетнутися лише в одній точці, але з чотирьох прямих, що утворюють краї дошки, вона перетинається лише з двома. Звідси витікає, що наша пряма перетинає прямі, що утворюють поля дошки, саме більше в 16 точках. Ці точки розбивають пряму не більше ніж на 15 відрізків, кожен з яких ув'язнений усередині якого-небудь поля. Таким чином, будь-який розріз дошки перетинає не більше 15 полів. З рис. 2.4 виходить, що рівно стільки полів перетинає розріз, проведений паралельно діагоналі дошки і що проходить через середини сторін двох кутових клітин.

Відповідь: рис. 2.4.

Задача 5. Скільки треба провести розрізів на дошці, щоб перетнути усі її поля?

Р озв'язання. Зрозуміло, вісім розрізів цілком достатньо — по одному уздовж кожної вертикалі або кожної горизонталі. Проте, виявляється, що і сім прямих можуть перетнути усі 64 поля дошки. Для цього одну пряму треба провести майже в діагональному напрямі через центр дошки, а шість інших — в напрямах майже паралельних другій діагоналі дошки (рис. 2.5).

Відповідь: рис. 2.5.

З

Рис. 2.5

адача 6. На яке максимальне число частин можна розрізати шахівницю, якщо вважати різними частини, що відрізняються своєю формою або кольором полів при поєднанні?

Р озв'язання. Максимальне число частин дорівнює 18. На мал. представлені два розрізи.

Р

Рис. 2.6.1

Рис. 2.6.2

ішення на рис. 2.6.1 належить Лойду; особливість його полягає в тому, що одна з частин містить вісім полів(максимум).

У рішенні на рис. 2.6.1, частини відрізняється зовнішньою симетрією, жодна частина не містить більше п'яти полів. На рис. 2.6.2 частини 17 і 18, або 8 і 9, хоча і мають однакову форму, відрізняються кольором полів при поєднанні.

Інші частини, наприклад, 3 і 6, взагалі не можуть бути поєднані (перевертати їх не можна).

Відповідь: 18.

Задача 7. Довести теорему Піфагора на шаховій дошці.

Розв'язання. Розіб'ємо дошку на квадрат і чотири однакові прямокутні трикутники (рис. 12, а). На рис. 12, б зображені ті ж чотири трикутники і два квадрати.

Рис. 2.7.1

Рис. 2.7.2

Трикутники в обох випадках займають одну і ту ж площу, і, отже, одну і ту ж площу займають частини дошки, що залишилися, без трикутників (на рис. 2.7.1 — один квадрат, а на рис. 2.7.2 — два). Оскільки великий квадрат побудований на гіпотенузі прямокутного трикутника, а маленькі — на його катетах, то знаменита теорема Піфагора доведена.

Відповідь: доведено.

Задача 8. Шахівницю розрізали на 4 частини, як показано на рис. 2.8.1, і склали з них прямокутник (рис. 2.8.2). Площа шахівниці, очевидно, дорівнює 64, а площа отриманого прямокутника — 65. Таким чином, при розрізанні дошки звідкись взялося «зайве» поле. Пояснити як так сталося.

Розв'язання. Розгадка полягає в тому, що наші креслення виконані не зовсім точно. Якщо робити креслення акуратно, то замість діагоналі прямокутника на мал. б з'явиться ромбовидна, трохи витягнута фігура із сторонами, які здаються такими, що майже злилися. Площа цієї фігури якраз і дає одне « зайве» поле.

Рис. 2.8.1

Рис. 2.8.2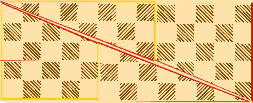

Відповідь: через неточне креслення.