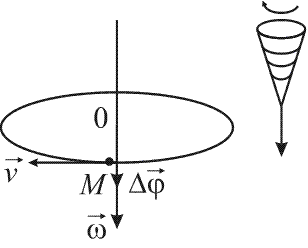
Основная задача механики - определить положение тел в пространстве в любой момент времени. Механическим движением называется изменение положения тела в пространстве относительно других тел с течением времени. Поступательное движение - движение, при котором в любой момент времени все точки данного тела движутся одинково. Враща́тельное движе́ние — когда все точки данного тела вравщаются вокруг одной оси. Материальная точка - физическая модель тела, размерами которого в данных условиях движения можно пренебречь. Рассматривается как точка, имеющая массу тела. Система отсчета (СО) - тело отсчета, система координат, связанная с ним, прибор для отсчета времени. Тело отсчета - произвольно выбранное тело, относительно которого определяется положение движущейся материальной точки (или тела).
-------------------------------------------------------------------------------
Радиус-вектор точки - это вектор, начало которого совпадает с началом системы координат, а конец - с данной точкой. Положение тела в пространстве задается радиус - вектором Траектория - воображаемая линия, вдоль которой движется тело. Путь - длина траектории. Средняя скорость u среднего движения равна среднему арифметическому начальной и конечной скоростей. Мгновенной скоростью называется скорость тела в данный момент времени. Vмгн=s/t Средняя скорость перемещения равна отношению полного перемещения к промежутку времени, за которое это перемещение совершено.
 где
Vср
-средняя скорость перемещения, -
перемещение, ∆ t - интервал времени.
Средняя
путевая скорость
равна отношению полного пути к промежутку
времени, за который этот путь пройден.
где
Vср
-средняя скорость перемещения, -
перемещение, ∆ t - интервал времени.
Средняя
путевая скорость
равна отношению полного пути к промежутку
времени, за который этот путь пройден.
 где
υср - средняя путевая скорость , l -
путь.
******
где
υср - средняя путевая скорость , l -
путь.
******
----------------------------------------------------------------------
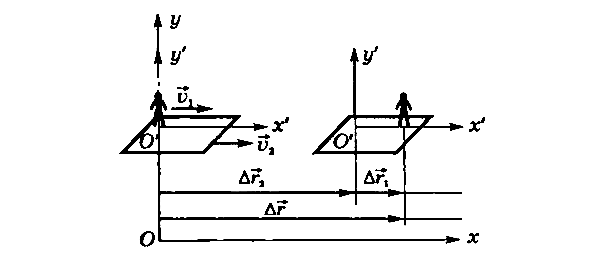
Относительность движения проявляется в том, что скорость, траектория и путь и некоторые другие характеристики движения относительны, то есть они могут быть различны в разных системах отсчета. Космонавт вышел в открытый космос. В состоянии покоя или движения он находится? Если рассматривать его относительно друга космонавта, находящегося рядом, он будет покоиться. А если относительно наблюдателя на Земле, космонавт движется с огромной скоростью. Аналогично с поездкой в поезде. Относительно людей в поезде вы неподвижно сидите и читаете книгу. Но относительно людей, которые остались дома, вы двигаетесь со скоростью поезда. Преобразования Галилея. Рассмотрим две системы отсчета движущиеся друг относительно друга и с постоянной скоростью v0.Одну из этих систем обозначим буквой K. Будем считать неподвижной. Тогда вторая система K¢ будет двигаться прямолинейно и равномерно. Выберем координатные оси x,y,z системы K и x',y',z' системы K' так что оси x и x' совпадали, а оси y и y' , z и z', были параллельны друг другу. Найдем связь между координатами x,y,z некоторой точки P в системе K и координатами x',y',z' той же точки в системе K'. Если начать отсчёт времени с того момента, когда начало координат системы, совпадали, то x=x'+v0, кроме того, очевидно, что y=y', z=z'. Добавим к этим соотношениям принятое в классической механике предположение, что время в обеих системах течёт одинаковым образом, то есть t=t'. Получим совокупность четырёх уравнений : x=x'+v0t;y=y';z=z';t=t', названных преобразованиями Галилея. Механический принцип относительности. Положение о том, что все механические явления в различных инерциальных системах отсчёта протекают одинаковым образом, вследствие чего никакими механическими опытами невозможно установить, покоится ли система или движется равномерно и прямолинейно носит названия принцип относительности Галилея. Нарушение классического закона сложения скоростей. Исходя из общего принципа относительности (никаким физическим опытом нельзя отличить одну инерциальною систему от другой), сформулированным Альбертом Эйнштейном, Лоуренс изменил преобразования Галилиея и получил : x'=(x-vt)/Ö (1-v2/c2); y'=y; z'=z; t'=(t-vx/c2)/Ö (1-v2/c2). Эти преобразования называются преобразованиями Лоуренса. Законы сложения скорости и перемещения. Перемещения и скорости тел, если одно едет по другому – складываются. Свяжем неподвижную систему отсчета (хОу) с Землей, а подвижную (х’О’у) — с пароходом



Равномерное движение - движение при котором материальная точка за любые равные промежутки времени совершает равные перемещения.
При
равномерном прямолинейном движении
скорость тела постоянна, ускорение
равно нулю. Траектория равномерного
прямолинейного движения - прямая
линия.
Уравнения
зависимости кинематических величин от
времени при равномерном прямолинейном
движении
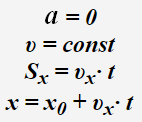 1.
График зависимости проекции скорости
от времени.
1.
График зависимости проекции скорости
от времени.
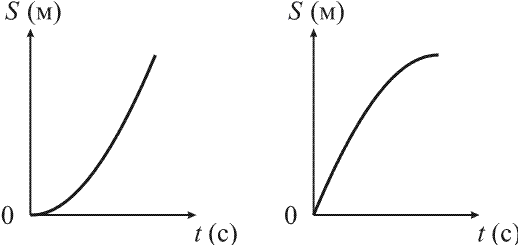
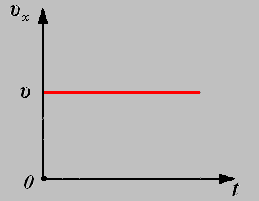 2.
График зависимости проекции перемещения
от времени
2.
График зависимости проекции перемещения
от времени
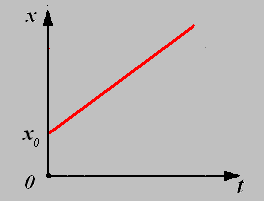
 3.
График зависимости координаты от
времени.
3.
График зависимости координаты от
времени.
-------------------------------------------------------------------
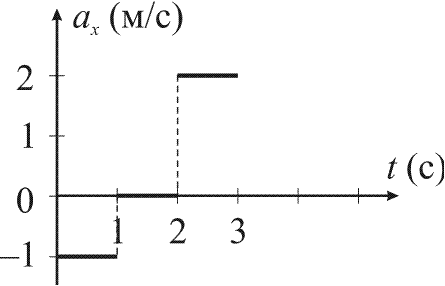
Ускорение - это величина, которая характеризует быстроту изменения скорости и равная отношению изменения скорости к промежутку времени. В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
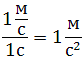 .
Равнопеременное
движение
– это движение, при котором скорость
тела (материальной точки) за любые
равные промежутки времени изменяется
одинаково. Ускорение тела при
равнопеременном движении остаётся
постоянным по модулю и по направлению
(a = const).
Равнопеременное движение
может быть равноускоренным или
равнозамедленным.
.
Равнопеременное
движение
– это движение, при котором скорость
тела (материальной точки) за любые
равные промежутки времени изменяется
одинаково. Ускорение тела при
равнопеременном движении остаётся
постоянным по модулю и по направлению
(a = const).
Равнопеременное движение
может быть равноускоренным или
равнозамедленным.
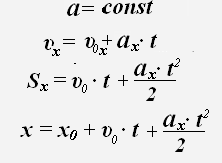 a=(v-v0)/t
a=(v-v0)/t


 Второй
закон Ньютона:
ускорение пропорционально действующей
силе (при заданной массе) и обратно
пропорционально массе (при заданной
силе).
a=F/m
Сила равна произведению
массы на ускорение.
F=ma
Второй
закон Ньютона:
ускорение пропорционально действующей
силе (при заданной массе) и обратно
пропорционально массе (при заданной
силе).
a=F/m
Сила равна произведению
массы на ускорение.
F=ma
-------------------------------------------------------------------------------------
Свобо́дное падéние — равноускоренное движение под действием силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы. Свободное падение тела происходит с ускорением 9,8 м/с2. Тело, подброшенное вверх, при отсутствии сопротивления воздуха тоже движется с постоянным ускорением, вызванным действием силы тяжести. Но в этом случае начальная скорость v0, которую телу придали при броске, направлена вверх, т. е. противоположно силе тяжести и ускорению свободного падения. Поэтому скорость тела уменьшается (за каждую секунду — на величину, численно равную модулю ускорения свободного падения, т. е. на 9,8 м/с). Через определенное время тело достигает наибольшей высоты и на какой-то момент останавливается, т. е. его скорость становится равной нулю. Понятно, что чем большую начальную скорость получило тело при броске, тем больше будет время подъема и тем на большую высоту оно поднимется к моменту остановки. Затем под действием силы тяжести тело начинает равноускоренно падать вниз. ***** ****
-----------------------------------------------------------------------------
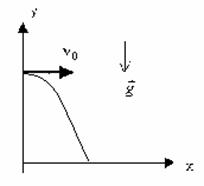
Движение тела, брошенного горизонтально. Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью (рис. 1). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ox и Oy. Начало отсчета координат совместим с начальным положением тела. Из рисунка 1 видно, что
 ax=0,
ay=-g
Тогда движение тела опишется
уравнениями:
ax=0,
ay=-g
Тогда движение тела опишется
уравнениями:
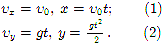
Анализ
этих формул показывает, что в горизонтальном
направлении скорость тела остается
неизменной, т. е. тело движется равномерно.
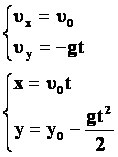 (вместо
у0 –
h)
(вместо
у0 –
h)
--------------------------------------------------------------------------
Движение тела, брошенного под углом к горизонту. Если тело бросить под углом к горизонту, то в полете на него действуют сила тяжести и сила сопротивления воздуха. Если силой сопротивления пренебречь, то остается единственная сила – сила тяжести. Поэтому вследствие 2-го закона Ньютона тело движется с ускорением, равным ускорению свободного падения ; проекции ускорения на координатные оси равны ах = 0, ау = -g. Любое сложное движение материальной точки можно представить как наложение независимых движений вдоль координатных осей, причем в направлении разных осей вид движения может отличаться. В нашем случае движение летящего тела можно представить как наложение двух независимых движений: равномерного движения вдоль горизонтальной оси (оси Х) и равноускоренного движения вдоль вертикальной оси (оси Y) (рис. 1).
Проекции
скорости тела, следовательно, изменяются
со временем следующим образом:
![]() где
– начальная скорость, α – угол
бросания.
Координаты тела, следовательно,
изменяются так:
где
– начальная скорость, α – угол
бросания.
Координаты тела, следовательно,
изменяются так:

 При
нашем выборе начала координат начальные
координаты (рис. 1) Тогда:
При
нашем выборе начала координат начальные
координаты (рис. 1) Тогда:
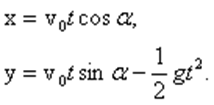 (1)
Проанализируем
формулы (1). Определим время движения
брошенного тела. Для этого положим
координату y равной нулю, т.к. в момент
приземления высота тела равна нулю.
Отсюда получаем для времени полета:
(1)
Проанализируем
формулы (1). Определим время движения
брошенного тела. Для этого положим
координату y равной нулю, т.к. в момент
приземления высота тела равна нулю.
Отсюда получаем для времени полета:
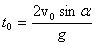 (2)
Из
уравнений (1) можно получить уравнение
траектории тела, т.е. уравнение, связывающее
координаты х и у тела во время движения.
Для этого нужно из первого уравнения
(1) выразить время:
(2)
Из
уравнений (1) можно получить уравнение
траектории тела, т.е. уравнение, связывающее
координаты х и у тела во время движения.
Для этого нужно из первого уравнения
(1) выразить время:
 и
подставить его во второе уравнение.
Тогда получим уравнение траектории:
и
подставить его во второе уравнение.
Тогда получим уравнение траектории:
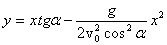
---------------------------------------------------------------------------------
9. Равномерное движение материальной точки по окружности. Период и частота вращения, их единицы. Угловая скорость, её связь с линейной скоростью (вывод обязателен!).
При равномерном движении т. М по окружности (рис. 33):
– модуль скорости не изменяется
|![]() 1|
= |
2|
1|
= |
2| ![]() v
v
![]() t =
0 ;
t =
0 ;
– направление вектора скорости изменяется
n = 0 .
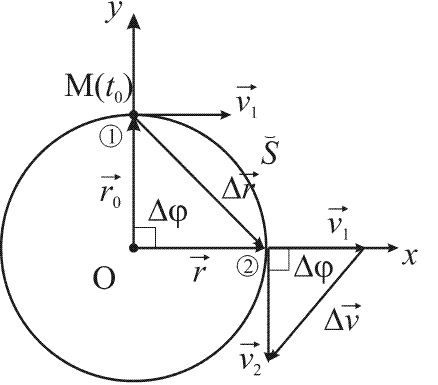
Рис. 33
Полное
ускорение в этом движении равно
нормальному ускорению
=
n и
направлено перпендикулярно к направлению
вектора скорости , по радиусу к центру
окружности. При этом движении радиусвектор
т. М поворачивается на угол ![]()
![]() =
–
0 за
интервал времени
t
= t – t0,
а его конец описывает дугу окружности
=
–
0 за
интервал времени
t
= t – t0,
а его конец описывает дугу окружности ![]() .
.
При
вращении угол поворота
изменяется
с течением времени, тогда уравнение
=
(t)
– это уравнение вращения. Угол
(или
)
аналогичен величине линейного пути S
при поступательном движении, и его
называют углом поворота или угловым
путем. Элементарное угловое перемещение
![]() –
это вектор, направленный вдоль оси по
правилу правого винта и численно равный
углу
.
Введем угловые кинематические
характеристики: угловую скорость
–
это вектор, направленный вдоль оси по
правилу правого винта и численно равный
углу
.
Введем угловые кинематические
характеристики: угловую скорость ![]() и
угловое ускорение
и
угловое ускорение ![]() при
вращении вокруг неподвижной оси .
при
вращении вокруг неподвижной оси .
Период - это время (полного оборота) и измеряется в единицах времени. Основная единица времени – секунда. Частота - это количество оборотов в единицу времени, например в секунду. И измеряется поэтому в обратных единицах 1/сек=Гц (герц) . В старой литературе можно изредка втретить единицу "цикл", 1 цикл=1 герцу. В технике часто пишут именно обороты в секунду, минуту, час: об/мин, об/сек Есть ещё КРУГОВАЯ (или УГЛОВАЯ) частота - угол, на который вращающееся тело поворачивается в секунду. Измеряется в радианах в секунду : рад/сек
Средняя угловая скорость cp – это физическая величина, равная отношению угла поворота к интервалу времени, за который оно произошло.
 .
(32)
.
(32)
Единицы угловой скорости в СИ и в системе СГС
 .
.
Мгновенная
угловая скорость
мгн –
это физическая величина, равная пределу
отношения углового перемещения
к
интервалу времени, за который оно
произошло (при
t ![]() 0).
0).
 .
(33)
.
(33)
Угловая скорость – производная от угла поворота по времени.
При равномерном движении по окружности вокруг закрепленной оси, при котором за любые равные промежутки времени радиус-вектор точки поворачивается на одинаковые углы, угловая скорость может рассматриваться как скаляр:
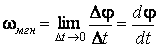 .
.
cpмгн = const
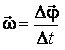 ;
;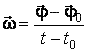 .
(34)
.
(34)
При
равномерном вращении модуль угловой
скорости:  .
.
Угловой путь: = w t.
Из формулы (34) следует уравнение равномерного движения материальной точки по окружности:
![]() .
(35)
.
(35)
или
![]() .
.
Направление вектора определяется по правилу буравчика : направление вращения буравчика, расположенного перпендикулярно плоскости вращения, совпадает с движением т. М по окружности, а его поступательное движение вдоль оси совпадает с направлением угловой скорости (рис. 34).
|
|
Рис. 34 |
|
Связь между линейной и угловой скоростью. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. При вращении твердого тела разные его точки имеют разные линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью какой-либо точки вращающегося тела и угловой скорость существует связь. Точка, лежащая на окружности радиуса R, за один оборот пройдет путь 2πR. А так как, время одного оборота тела есть период Т, то модуль линейной скорости можно найти так: v=2πR/T=2πRν или v=ωR. Отсюда видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Модуль ускорения точки, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: a=v2/R, но v=ωR. Следовательно, a=ω2R. Чем дальше расположена точка твердого тела от оси вращения, тем больше по модулю ускорение он имеет. Скорость тела, направленную по касательной к окружности, называют линейной. Угловой скоростью w называют величину, равную отношению угла поворота Df радиуса-вектора точки, движущейся по окружности к промежутку времени Dt, в течение которого произошел этот поворот Угловая и линейная скорости связаны соотношением V = w·R.
. Центростремительное ускорение: вывод формулы.
an=v2R
или
an=ω2R ,
где an — нормальное (центростремительное) ускорение, v — (мгновенная) линейная скорость движения по траектории, ω — (мгновенная) угловая скорость этого движения относительно центра кривизны траектории, R — радиус кривизны траектории в данной точке. (Связь между первой формулой и второй очевидна, учитывая v=ωR ).
Выражения выше включают абсолютные величины. Их легко записать в векторном виде, домножив на eR — единичный вектор от центра кривизны траектории к данной ее точке:
an=v2ReR=v2R2R
an=ω2R.
Эти формулы равно применимы к случаю движения с постоянной (по абсолютной величине) скоростью, так и к произвольному случаю. Однако во втором надо иметь в виду, что центростремительное ускорение не есть полный вектор ускорения, а лишь его составляющая, перпендикулярная траектории (или, что то же, перпендикулярная вектору мгновенной скорости); в полный же вектор ускорения тогда входит еще и тангенциальная составляющая (тангенциальное ускорение) aτ=dv/dt , по направлению совпадающее с касательной к траектории (или, что то же, с мгновенной скоростью).
Разложение ускорения на тангенциальную и нормальную компоненты (вторая из которых и есть центростремительное или нормальное ускорение) можно найти, продифференцировав по времени вектор скорости, представленнный в виде v=veτ через единичный вектор касательной eτ:
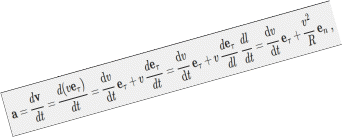 Где
первое слагаемое — тангенциальное
ускорение,
а второе — нормальное
ускорение.
Где
первое слагаемое — тангенциальное
ускорение,
а второе — нормальное
ускорение.
Здесь использовано обозначение en для единичного вектора нормали к траектории и l — для текущей длины траектории (l=l(t) ); в последнем переходе также использовано очевидное dl/dt=v .
Далее можно просто формально назвать член
v2Ren
— нормальным (центростремительным) ускорением. При этом его смысл, смысл входящих в него объектов, а также доказательство того факта, что он действительно ортогонален касательному вектору (то есть что en — действительно вектор нормали) — будет следовать из геометрических соображений (впрочем, то, что производная любого вектора постоянной длины по времени перпендикулярна самому этому вектору, — достаточно простой факт; в данном случае мы применяем это утверждение для deτdt.
------------------------------------------------------------------------------------
11. Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии. По криволинейным траекториям движутся планеты, воды рек.
Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам
![]()
![]()
![]()
![]()
![]()
тангенциа́льное ускоре́ние — компонента ускорения, направленная по касательной к траектории движения. Характеризует изменение модуля скорости в отличие отнормальной компоненты, характеризующей изменение направления скорости. Тангенциальное ускорение равно произведению единичного вектора, направленного по скорости движения, на производную модуля скорости по времени. Таким образом, направлено в ту же сторону, что и вектор скорости при ускоренном движении (положительная производная) и в противоположную при замедленном (отрицательная производная).
Величину тангенциального ускорения как проекцию вектора ускорения на касательную к траектории можно выразить так:
aτ=dvdt,
где v =dl/dt — путевая скорость вдоль траектории, совпадающая с абсолютной величиной мгновенной скорости в данный момент.
Если использовать для единичного касательного вектора обозначение eτ , то можно записать тангенциальное ускорение в векторном виде:
aτ=dvdteτ.
Центростремительное ускорение(нормальное) — компонента ускорения точки, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной (вторая компонента, тангенциальное ускорение, характеризует изменение модуля скорости). Направлено к центру кривизны траектории, чем и обусловлен термин. По величине равно квадрату скорости, поделённому на радиус кривизны. Термин «центростремительное ускорение» эквивалентен термину «нормальное ускорение». Ту составляющую суммы сил, которая обуславливает это ускорение, называют центростремительной силой.
Наиболее простым примером центростремительного ускорения является вектор ускорения при равномерном движении по окружности (направленный к центру окружности).
В классической механике центростремительное ускорение вызывается компонентами сил, направленными ортогонально вектору скорости, и, следовательно, оно перпендикулярно касательной к траектории в данной точке. Например, кривизна орбит космических объектов характеризуется центростремительным ускорением, вызванным гравитацией.
Связанное понятие для неинерциальных систем отсчёта — центробежная сила.
Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости движения материальной точки по окружности.
При вращении точки вокруг неподвижной оси, угловое ускорение по модулю равно[1]:
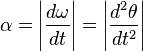
При вращательном
движении тела вектор углового
ускорения ![]() направлен
вдоль оси вращения (в сторону
направлен
вдоль оси вращения (в сторону ![]() при
ускоренном вращении и противоположно
—
при замедленном).
при
ускоренном вращении и противоположно
—
при замедленном).
При вращении
вокруг неподвижной точки вектор углового
ускорения определяется как первая
производная от вектора угловой
скорости ![]() по
времени[2],
то есть
по
времени[2],
то есть
![]() ,
,
и направлен по касательной к годографу вектора в соответствующей его точке.
Существует связь между тангенциальным и угловым ускорениями:
![]() ,
,
где R — радиус кривизны траектории точки в данный момент времени. Итак, угловое ускорение равно второй производной от угла поворота по времени или первой производной от угловой скорости по времени.
Угловое ускорение измеряется в рад/с².
Уравнения движения и зависимость угловой скорости от времени
При равноускоренном движении материальной точки по окружности уравнение движения (зависимость углового положения точки от времени φ(t)) и закон изменения угловой скорости с течением времени ω(t) по форме совпадают с соответствующими уравнениями для равноускоренного прямолинейного движения:
φ(t)=φ0+ω0t+βt22, ω(t) = ω0 + βt,
где φ0 — угловое положение материальной точки в начальный момент времени; ω0 — величина начальной угловой скорости; β — модуль углового ускорения.
При равнозамедленном движении материальной точки по окружности уравнение движения φ(t) и закон изменения скорости ω(t) записываются по аналогии с соответствующими уравнениями для равнозамедленного прямолинейного движения:
φ(t)=φ0+ω0t−βt22, ω(t) = ω0 − βt,
где φ0 — угловое положение материальной точки в начальный момент времени; ω0 — величина начальной угловой скорости; β — модуль углового ускорения.
-------------------------------------------------------------------------------------------------------------------------------
12.
В инерциальных
системах отсчета сохраняется закон
инерции. В неинерциальных
– не сохраняется. Любая система,
движущаяся с ускорением относительно
инерциальной системы отсчёта, является
неинерциальной. (Пример с разгоном и
остановкой автобуса и шариком внутри
него.)
Масса тела – скалярная физическая
величина, численно равная отношению
равнодействующих сил, приложенных к
предмету на ускорение
 [кг]
В СИ массу обозначают за килограмм.
[кг]
В СИ массу обозначают за килограмм.
---------------------------------------------------------------------------------------------
13. Первый
закон Ньютона
Существуют
такие системы отсчета, относительно
которых тела сохраняют скорость
неизменной, если на них не действуют
другие тела.
Второй
закон ньютона
Ускорение
тела прямо пропорционально равнодействующих
сил, приложенных к нему, и обратно
пропорционально его массе
![]() где
где
![]() - ускорение тела
- ускорение тела
![]() - равнодействующая всех сил, приложенных
к телу
- равнодействующая всех сил, приложенных
к телу
![]() - масса тела.
Третий
закон Ньютона
Силы,
с которыми два тела действуют друг на
друга, равны по величине и противоположны
по направлению.
- масса тела.
Третий
закон Ньютона
Силы,
с которыми два тела действуют друг на
друга, равны по величине и противоположны
по направлению.
![]() Закон
утверждает, что силы возникают лишь
попарно, причём любая сила, действующая
на тело, имеет источник происхождения
в виде другого тела. Иначе говоря, сила
всегда есть результат взаимодействия
тел. Существование сил, возникших
самостоятельно, без взаимодействующих
тел, невозможно
Система, в которой
тела взаимодействуют, должна быть
замкнутой!!!
Закон
утверждает, что силы возникают лишь
попарно, причём любая сила, действующая
на тело, имеет источник происхождения
в виде другого тела. Иначе говоря, сила
всегда есть результат взаимодействия
тел. Существование сил, возникших
самостоятельно, без взаимодействующих
тел, невозможно
Система, в которой
тела взаимодействуют, должна быть
замкнутой!!!
----------------------------------------------------------------------------------------------
14. Силы
в механике
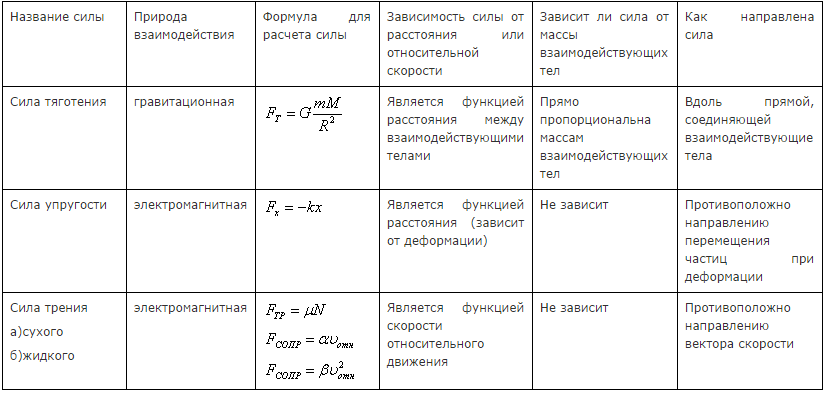 Несмотря
на кажущееся многообразие сил в природе,
их можно разделить на четыре типа,
которые определяют все природные
явления:
Несмотря
на кажущееся многообразие сил в природе,
их можно разделить на четыре типа,
которые определяют все природные
явления:
1. Гравитационные; к ним относятся сила тяжести тяготения. Вид взаимодействия - только притяжение. 2. Электромагнитные силы; к ним относятся: сила упругости, сила трения, сила тяги. Посредством действия этих сил возможно как притяжение, так и отталкивание. Это взаимодействие преобладает внутри вещества и обусловлено взаимодействием молекул и атомов. 3. Ядерные силы; проявляются внутри атомного ядра. 4. Слабые силы; проявляются при взаимодействии элементарных частиц. В механике Ньютона можно рассматривать только гравитационное и электромагнитное взаимодействия. В отличие от короткодействующих ядерного и слабого взаимодействия, гравитационное и электромагнитное взаимодействия – дальнодействующие: их действия проявляются на очень больших расстояниях. Мы будем рассматривать только две природы сил: электромагнитную и гравитационную. Природа силы трения - электромагнитная. Это означает, что причиной её возникновения являются силы взаимодействия между частицами, из которых состоит вещество и они должны обладать зарядом. гравитационные силы, которые действуют между телами, имеющими массу.
15. Гравита́ция (притяжение, всеми́рное тяготе́ние, тяготе́ние) (от лат. gravitas — «тяжесть») — универсальное фундаментальное взаимодействие между всеми материальными телами. В приближении малых скоростей и слабого гравитационного взаимодействия описывается теорией тяготения Ньютона, в общем случае описывается общей теорией относительности Эйнштейна.
(Зако́н
всемирного тяготе́ния Ньютона) —
закон, описывающий гравитационное
взаимодействие в
рамках классической
механики.
Этот закон был открыт Ньютоном около
1666 года. Он гласит, что сила ![]() гравитационного
притяжения между двумя материальными
точками массы
гравитационного
притяжения между двумя материальными
точками массы ![]() и
и ![]() ,
разделёнными расстоянием
,
разделёнными расстоянием ![]() ,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть:
,
пропорциональна обеим массам и обратно
пропорциональна квадрату расстояния
между ними — то есть:
![]()
Здесь ![]() — гравитационная
постоянная,
равная 6,67384(80) * 10-11 м³/(кг
с²).
— гравитационная
постоянная,
равная 6,67384(80) * 10-11 м³/(кг
с²).
Кавендиш
утверждал, что он взвесил Землю, хотя
он только измерил коэффициент ![]() ;
но это единственный способ определить
массу Земли.
;
но это единственный способ определить
массу Земли.
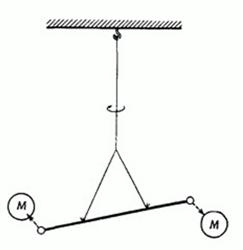 .
.
Упрощенная схема прибора, использованного Кавендишем для проверки закона всемирного тяготения для малых тел и измерения постоянной тяготения .