3. Варианты контрольной работы
Задача 1
Используя необходимое и достаточной
условие устойчивости, выяснить, будет
ли замкнутая САУ устойчива, если ее
характеристическое уравнение имеет
вид
,
а значения коэффициентов уравнения
приведены в табл.2.
Таблица 2
№ варианта |
a0 |
a1 |
a2 |
a3 |
0 |
3 |
6 |
1 |
2 |
1 |
4 |
8 |
1 |
2 |
2 |
6 |
6 |
1 |
1 |
3 |
5 |
10 |
1 |
2 |
4 |
1,5 |
3 |
1 |
2 |
5 |
2,5 |
5 |
1 |
2 |
6 |
3,5 |
7 |
1 |
0 |
7 |
4,5 |
9 |
1 |
2 |
8 |
5 |
5 |
2 |
2 |
9 |
4 |
1 |
1 |
0 |
Задача 2
Будет ли замкнутая САУ устойчива (по критерию Гурвица), если ее характеристическое уравнение имеет вид .
Значения коэффициентов уравнения приведены в табл.3.
Таблица 3
№ варианта |
a0 |
a1 |
a2 |
a3 |
a4 |
0 |
4 |
3 |
1 |
5 |
2 |
1 |
6 |
2 |
0,5 |
3 |
3,5 |
2 |
0,96 |
0,8 |
0,3 |
0,1 |
0,12 |
3 |
2,8 |
3,4 |
1,6 |
0,4 |
1,25 |
4 |
0,6 |
0,3 |
0,2 |
1,5 |
0,35 |
5 |
5,8 |
3 |
7,5 |
2 |
1 |
6 |
3,4 |
4,4 |
2,5 |
1 |
5,7 |
7 |
2,5 |
1 |
0,8 |
3,5 |
0,14 |
8 |
0,55 |
1,5 |
0,7 |
3,2 |
2,6 |
9 |
1,2 |
2,7 |
3,6 |
0,8 |
5,4 |
Задача 3
Используя критерий Гурвица, записать условие устойчивости для замкнутой системы регулирования. Структурная схема системы представлена на рис. 4, выражения для передаточных функций приведены в табл.4.
Таблица 4
№ варианта |
W1(p) |
W2(p) |
W3(p) |
W4(p) |
0 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
Продолжение табл.4
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
Задача 4
По известной передаточной функции разомкнутой системы выяснить, будет ли замкнутая система устойчива. При решении использовать критерий Михайлова.
Структурная схема САУ изображена на
рис.5, передаточная функция разомкнутой
системы имеет вид
,
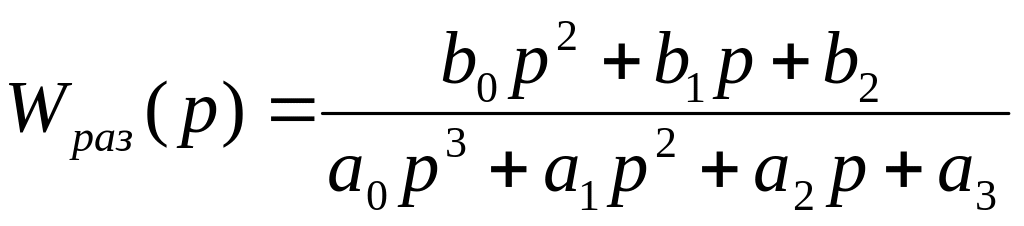значения коэффициентов приведены в
табл.5.
Рис.5 Структурная схема САУ к задаче 4
Таблица 5
№ варианта |
a0 |
a1 |
a2 |
a3 |
b0 |
b1 |
b2 |
0 |
1 |
1 |
-2 |
2 |
1 |
7 |
1 |
1 |
1 |
2 |
-3 |
1 |
2 |
8 |
2 |
2 |
1 |
3 |
-1 |
-1 |
3 |
5 |
3 |
3 |
1 |
1 |
-1 |
-2 |
4 |
6 |
4 |
4 |
1 |
2 |
2 |
2 |
5 |
3 |
1 |
5 |
1 |
3 |
-2 |
1 |
1 |
4 |
2 |
6 |
1 |
1 |
2 |
-1 |
2 |
1 |
3 |
Продолжение табл 5
7 |
1 |
2 |
2 |
-2 |
3 |
2 |
4 |
8 |
1 |
3 |
3 |
2 |
4 |
1 |
1 |
9 |
1 |
1 |
-3 |
1 |
1 |
8 |
2 |
Задача 5
Используя следствие из критерия
Михайлова, выяснить, будет ли замкнутая
система устойчива. Характеристическое
уравнение замкнутой системы имеет вид
,
значения коэффициентов уравнения
приведены в табл.6.
Таблица 6
№ варианта |
a0 |
a1 |
a2 |
a3 |
a4 |
a5 |
0 |
2 |
1 |
5 |
4 |
3 |
1 |
1 |
2 |
5 |
4 |
8 |
1 |
2 |
2 |
3 |
4 |
6 |
6 |
1 |
1 |
3 |
4 |
4 |
5 |
7 |
1 |
2 |
4 |
2 |
2 |
5 |
3 |
3 |
1 |
5 |
3 |
2 |
6 |
3 |
1 |
1 |
6 |
3 |
1 |
6 |
4 |
1 |
1 |
7 |
2 |
1 |
8 |
4 |
5 |
2 |
8 |
2 |
1 |
8 |
6 |
5 |
3 |
9 |
2 |
1 |
4 |
6 |
1 |
3 |