2. Пример выполнения контрольной работы

Контрольная работа состоит их пяти задач, в которых требуется оценить устойчивость САУ.

При решении первой задачи следует использовать необходимое и достаточное условие устойчивости, во второй и третьей задачах - критерий Гурвица, в четвертой – критерий Михайлова, в пятой – следствие из критерия Михайлова.

Пример 1

Используя необходимое и достаточной условие устойчивости, выяснить, будет ли замкнутая САУ устойчива, если ее характеристическое уравнение имеет вид .

Решение:

Необходимое и достаточное условие устойчивости для САУ любого порядка формулируется следующим образом: для того, чтобы замкнутая система была устойчива необходимо и достаточно, чтобы корни ее характеристического уравнения находились в левой полуплоскости комплексной плоскости переменной p.

Найдем корни уравнения .

Для этого сгруппируем слагаемые и вынесем общие множители за скобку .

Приравнивая к нулю каждый множитель, получаем

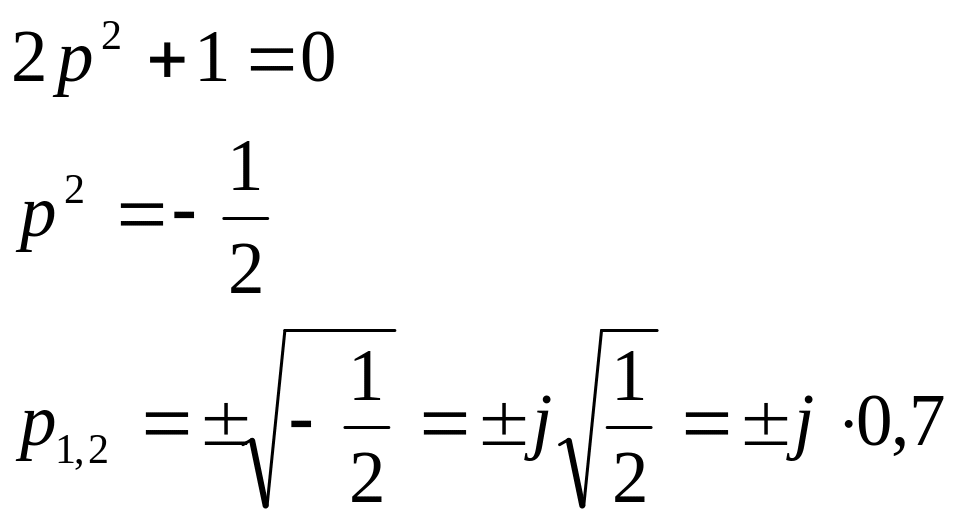и

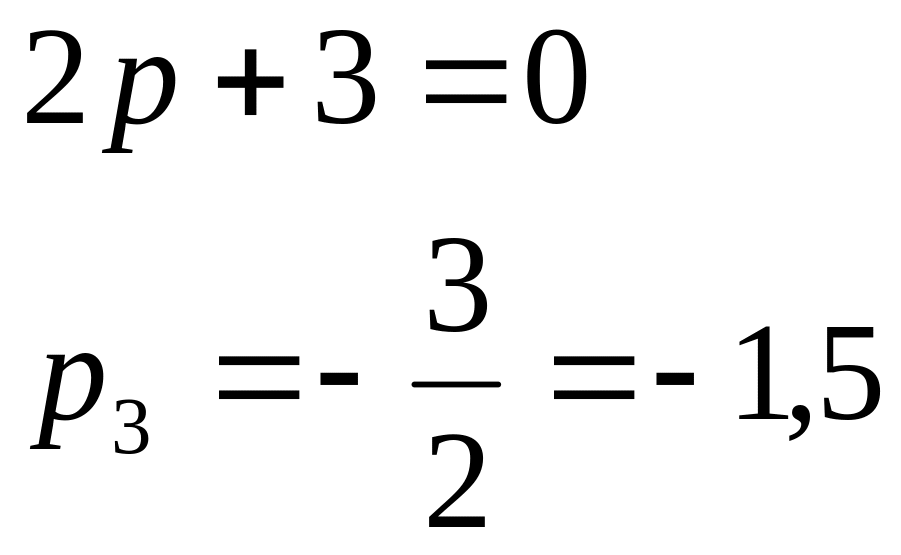
Получили три корня: два мнимых , , и один действительный .

Изобразим эти корни на комплексной плоскости (рис.4).

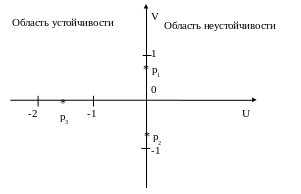
Рис.4 Иллюстрация к примеру 1

Из рисунка видно, что два корня расположены на колебательной границе устойчивости, а один корень уравнения в области устойчивости.

Ответ: система находится на колебательной границе устойчивости (система неустойчива).

Пример 2

Будет ли замкнутая САУ устойчива (по критерию Гурвица), если ее характеристическое уравнение имеет вид ?

Решение:

Запишем условие устойчивости САУ 4-го порядка в соответствии с критерием Гурвица (табл.1):

.

Подставим в систему неравенств численные значения коэффициентов характеристического уравнения , , , , . Так как все коэффициенты отличны от нуля и положительные, то достаточно проверить выполнение последнего неравенства:

.

Так как неравенство не выполняется, то САУ неустойчива.

Ответ: замкнутая САУ неустойчива.

Пример 3

Используя критерий Гурвица, записать условие устойчивости для замкнутой системы регулирования.

Структурная схема системы имеет вид

Выражения для передаточных функций заданы:

, , , .

Решение:

Чтобы применить критерий Гурвица, прежде всего, следует получить характеристическое уравнение замкнутой системы регулирования.

Найдем передаточную функцию замкнутой САУ, имеющей структурную схему, изображенную выше, и заданные передаточные функции элементов

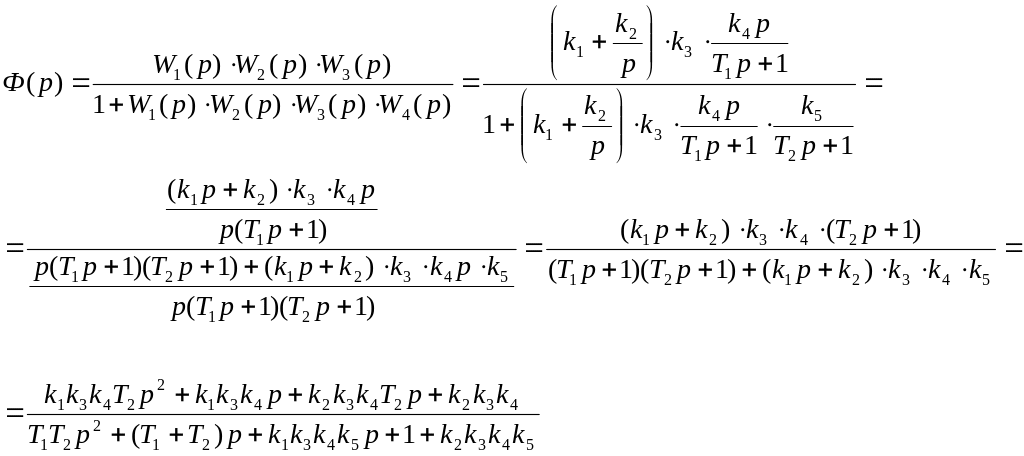
Характеристическое уравнение получим, приравняв к нулю знаменатель передаточной функции замкнутой системы:

Получили уравнение 2-го порядка, для которого условие устойчивости по критерию Гурвица можно записать в виде системы неравенств (табл.1)

,

подставляя значения коэффициентов характеристического уравнения , , , окончательно запишем

.

Проанализируем полученную систему неравенств. Известно, что параметры передаточных функций элементов имеют конкретный физический смысл. Так - постоянные времени элементов, величины, характеризующие их инерционные свойства, измеряются в единицах времени и всегда положительные, - коэффициенты передачи (усиления) элементов, показывают во сколько раз сигнал на выходе элемента будет изменяться по сравнению с сигналом на входе, могут принимать положительные и отрицательные значения. Таким образом, первое неравенство выполняется всегда, а второе можно преобразовать, тогда получим .

Ответ: условие устойчивости замкнутой САУ в соответствии с критерием Гурвица имеет вид .

Пример 4

По известной передаточной функции разомкнутой системы выяснить, будет ли замкнутая система устойчива. При решении использовать критерий Михайлова.

Структурная схема САУ имеет вид

Передаточная функция разомкнутой системы определяется выражением .

Решение:

Чтобы применить критерий Михайлова, прежде всего, следует получить характеристическое уравнение замкнутой системы регулирования.

Получить характеристическое уравнение можно способом, изложенным в примере 3, получив сначала передаточную функцию замкнутой САУ, а затем приравняв к нулю ее знаменатель. Также можно воспользоваться приемом, позволяющим получить характеристическое уравнение по известной передаточной функции разомкнутой САУ.

С учетом структуры передаточная функция замкнутой САУ имеет вид:

,

тогда характеристический полином , а характеристическое уравнение получим, приравняв его к нулю.

Для нашего примера

.

Как известно, дробь равна нулю, когда числитель равен нулю, а знаменатель не равен нулю. Получаем характеристическое уравнение замкнутой САУ .

На основе вышеизложенного можно сформулировать правило получения характеристического уравнения по известной передаточной функции разомкнутой системы: характеристическое уравнение замкнутой САУ с отрицательной обратной связью получают, приравняв к нулю сумму числителя и знаменателя передаточной функции разомкнутой системы.

Чтобы применить критерий Михайлова для оценки устойчивости замкнутой САУ, необходимо построить характеристический годограф. Для этого выполним замену и разложим уравнение на действительную и мнимую части.

При возведении мнимой единицы j в различные степени получают следующие значения: , , , и т.д.

,

.

Следует помнить, что при разложении комплексного числа в действительную часть входят те слагаемые, в которых нет мнимой единицы j, а в мнимую – те слагаемые, которые содержат мнимую единицу j, но без нее, с учетом знака.

(4)

Теперь, изменяя ω от 0 до ∞, можно рассчитать значения , и построить график характеристического годографа. При расчете значений частоты и построении графика можно воспользоваться средствами вычислительной техники, при этом следует лишь определиться с шагом изменения частоты и моментом окончания расчета. А можно использовать приближенный инженерный подход, позволяющий по наименьшему числу точек с допустимой погрешностью ответить на вопрос «устойчива система или нет».

Проанализируем, как должен выглядеть график частотного годографа устойчивой САУ 3-го порядка.

Из графика (рис.5) видно, что характерными являются 4 точки:

1 точка, в которой ω=0;

2 точка, в которой ;

3 точка, в которой ;

4 точка, в которой ω=∞.

Составим таблицу значений и и занесем в нее исходные данные для расчета:

№ точки	ω
1	0
2		0
3			0
4	∞

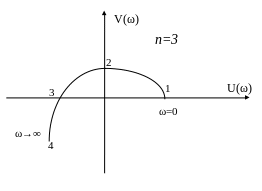
Рис.5 Иллюстрация к примеру 4

Используя систему уравнений (4), можно легко заполнить пустые ячейки таблицы.

Для точки 1 (ω=0):

.

Для точки 2 ( ):

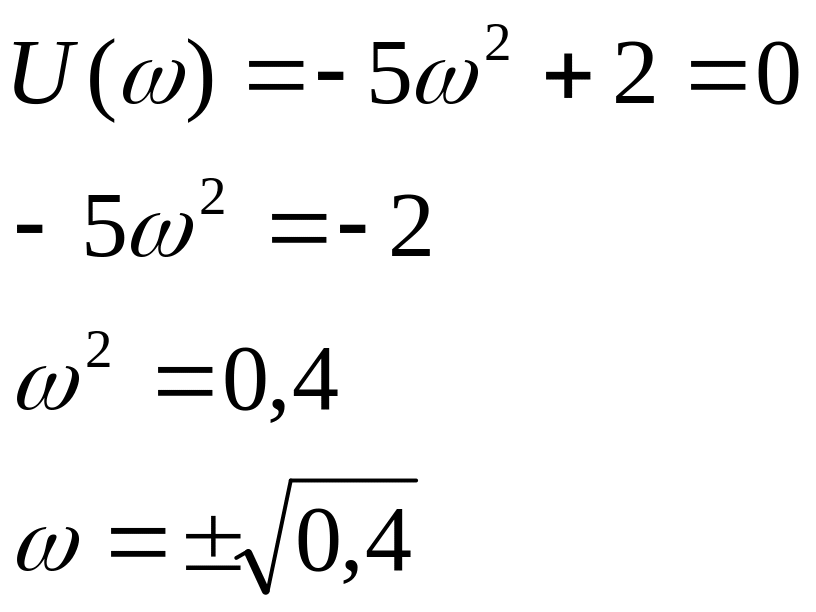
Так как рассматриваем изменение частоты от 0 до ∞, то выбираем только одно значение частоты - , тогда .

Для точки 3 ( ):

.

Значение ω=0 соответствует 1 точке, мы его уже рассмотрели, а из двух оставшихся значений выбираем положительное , т.к. рассматриваем изменение частоты от 0 до ∞. Тогда .

Для точки 4 (ω=∞):

.

Таблица значений и примет вид:

№ точки	ω
1	0	2	0
2	0,63	0	1,64
3	1,7	-13	0
4	∞	-∞	-∞

По данным выделенной части таблицы (без учета масштаба) построим график (рис.6).

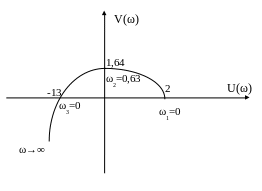
Рис.6 Характеристический годограф Михайлова

Из графика видно, что все признаки устойчивости в соответствии с критерием Михайлова выполняются, следовательно, САУ устойчива.

Ответ: САУ устойчива.

Пример 5

Используя следствие из критерия Михайлова, выяснить, будет ли замкнутая система устойчива. Характеристическое уравнение замкнутой системы имеет вид .

Решение:

Исследование системы на устойчивость на основе следствия из критерия Михайлова связано с анализом корней уравнений и , полученных приравниванием к нулю действительной и мнимой частей характеристического уравнения замкнутой САУ .

Выполним замену и разложим уравнение на действительную и мнимую части.

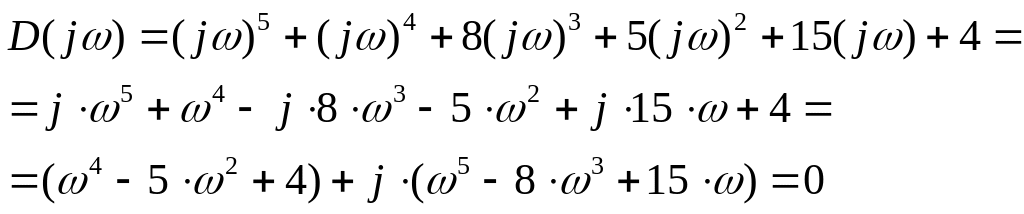
Тогда

.

Найдем корни уравнений и .

1). - биквадратное уравнение. Выполним замену и решим уравнение относительно новой переменной.

, .

Вернемся к переменной ω с учетом замены, тогда решение первого уравнения дает корни действительной части характеристического уравнения , , , .

2). .

Первый корень уравнения - . Чтобы найти остальные корни, решим биквадратное уравнение. Выполним замену и перейдем к новой переменной.

, .

Вернемся к переменной ω с учетом замены, тогда решение второго уравнения дает корни мнимой части характеристического уравнения , , , .

Полученные корни уравнений – вещественные, проверим, являются ли они чередующимися. Будем рассматривать только положительные корни (рис.3), т.к. если они чередуются, то и отрицательные, которые им симметричны, также будут чередоваться.

Корни уравнений оказались чередующимися.

Кроме того, следует проверить второе условие устойчивости в соответствии со следствием из критерия Михайлова: при ω=0 мнимая часть должна быть равна нулю, ее первая производная и действительная часть должны быть положительными , , .

,

,

.

Все условия выполняются, следовательно, система устойчива.

Ответ: САУ устойчива.