Лабораторная работа №1. Исследование модели предметной области.

Цель работы:

Разработать модель предметной области в виде множества непрерывных признаков пространства R³ и множества объектов, определенных в R³. Определить качество решения задачи классификации для различных методов анализа данных.

Необходимое оборудование и материалы.

- ОС Windows 98 (XP, 2000)

- MathLab 6.5( 7.0.)

- ПК класса не ниже Pentium IV, RAM 256Mb.

Трудоемкость: 8 академических часов.

Теоретический раздел

Байесов классификатор.

Рассмотрим пространство Rⁿ , которое содержит n координат. Каждый пример этого пространства Х задан значениями по всем координатам Х=<x1,x2,…,xn>. Пусть задано описание образа такое, что характер распределения примеров для классов С1, С2 имеет следующий вид:

fx(X|C1)=1/(2*Pi* D₁²) * exp( -1/(2*D₁²)*||X-M₁||²)

fx(X|C2)=1/(2*Pi* D₂²) * exp( -1/(2*D₂²)*||X-M₂||²), где

fx(X|C1)- функция плотности условной вероятности для класса С1,

fx(X|C2)- функция плотности условной вероятности для класса С2,

D₁^{2 –} дисперсия класса С1, M_{1 –} вектор средних значений по всем признакам класса С1, ||.|| - оператор вычисления расстояния по Евклиду,

D₂^{2 –} дисперсия класса С2, M_{2 –} вектор средних значений по всем признакам класса С2.

Необходимо определить положение границы между образами С1 и С2.

Байесовский классификатор опирается на нахождение оптимальной границы решений между образами с использованием критерия отношения правдоподобия

(Х)> для класса С1, где

(Х)= fx(X|C1)/fx(X|C2), =р1/р2,

р_i – априорная вероятность класса Сi.

Таким образом, пример Х относится к классу С1, если отношение правдоподобия (Х) больше порога  .

Рис. 1. Схема классификация по байесу для одномерного пространства примеров.

Байесов классификатор строит идеальную границу в случае линейно разделимых нормально распределенных моделей.

Обозначим символом е – множество результатов некорректной классификации. Тогда вероятность ошибки Ре классификатора работающего на основе байесовского решающего правила, можем определить в виде

P_e(C1,C2) = p1 P(e|C1) + p2 P(e|C2’), где

P(e|Ci) – условная вероятность ошибки для входного вектора класса i,

рi – априорная вероятность класса Сi , , - число объектов в обоих классах.

Условная вероятность ошибки - это ошибка отнесения объекта к классу приведенная к общему числу примеров этого класса.

Вероятность правильной классификации Р=1-Ре.

Для модельного пространства с ассиметричным распределением использовать усреднение дисперсии по левой и правой части

Усреднение с учетом априорной вероятности пары классов по всей выборке классов:

Ni – число объектов i-ого класса

N- общее число объектов

,

М – число пар классов.

Практическая часть

Следует предусмотреть формирование в модели более чем 1-го класса объектов. Распределение примеров для каждого класса по шкале признака должно соответствовать:

Вариант 1. Симметричное распределение и небольшие значения дисперсии.

fx(X|C1)=1/(2*Pi* D₁²) * exp( -1/(2*D₁²)*||X-M₁||²)

fx(X|C2)=1/(2*Pi* D₂²) * exp( -1/(2*D₂²)*||X-M₂||²), где

fx(X|C1)- функция плотности условной вероятности для класса С1,

fx(X|C2)- функция плотности условной вероятности для класса С2,

D₁^{2 –} дисперсия класса С1, M_{1 –} вектор средних значений по всем признакам класса С1, ||.|| - оператор вычисления расстояния по Евклиду,

D₂^{2 –} дисперсия класса С2, M_{2 –} вектор средних значений по всем признакам класса С2.

Вариант 2. Симметричное распределение и большая дисперсия.

Пример и последовательность действий.

1. Построить модель данных с несколькими кластерами (2 кластера) и 3000 объектов-примеров для 5-х координат за счет использования функции нормального распределения значений из заданного центра с установленным размахом.

R = normrnd(MU,SIGMA,M,N)

MU – математическое ожидание случайной величины,

SIGMA – параметр нормального закона (среднеквадратичное отклонение) регулирует разброс значений от мат.ожидания.,

М – число строк данных,

N – число столбцов.

Пример (для 2-х координат и 2-х кластеров) :

x=normrnd(10,2,750,1);

y=normrnd(20,5,750,1);

plot(x,y,'.r')

результат работы на Рис.2.

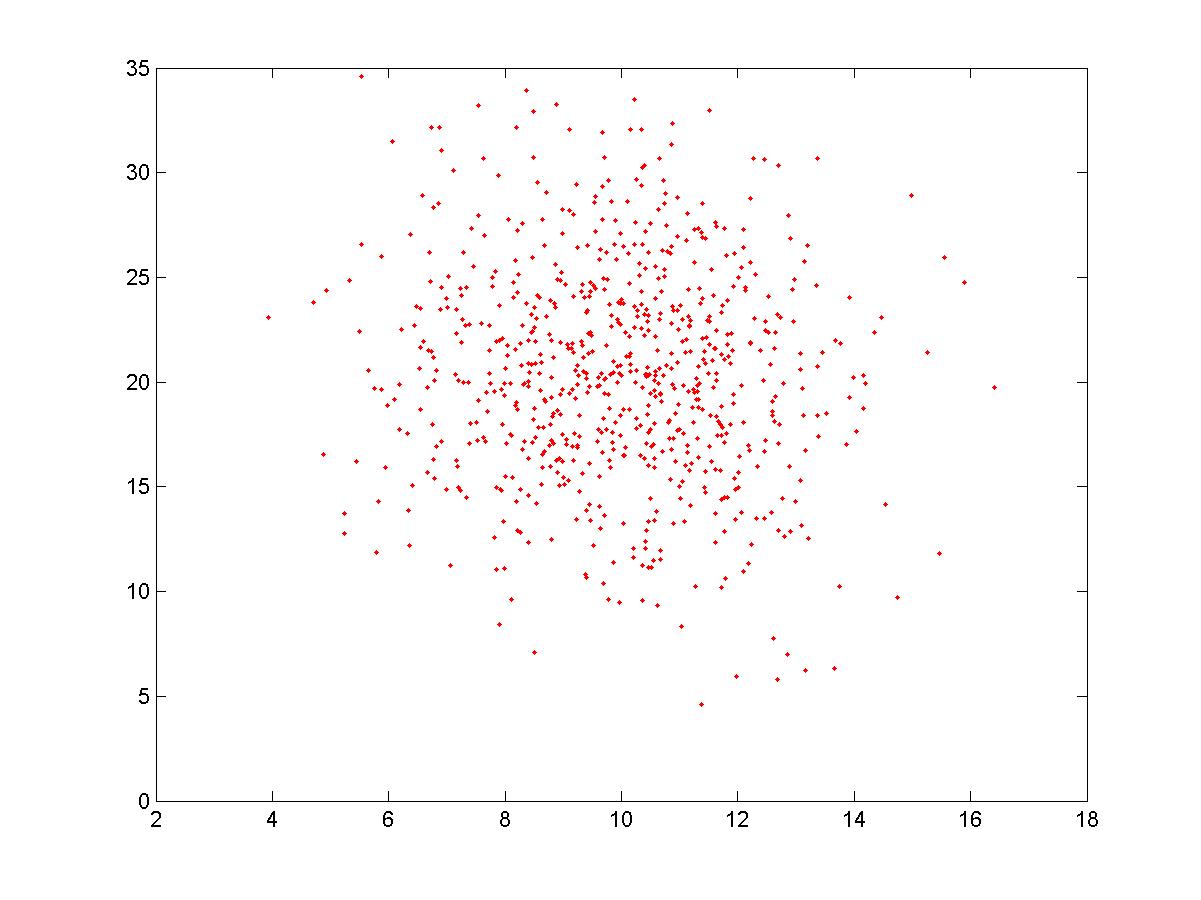
Рис.2. Кластер с центром в (10, 20)

Аналогично можно построить сколько угодно кластеров

Пример:

x=normrnd(10,2,750,1);

y=normrnd(20,5,750,1);

y1=normrnd(5,5,750,1);

x1=normrnd(0,2,750,1);

x=[x; x1];

y=[y; y1];

plot(x,y, '.r' )

Результат на рис.3.

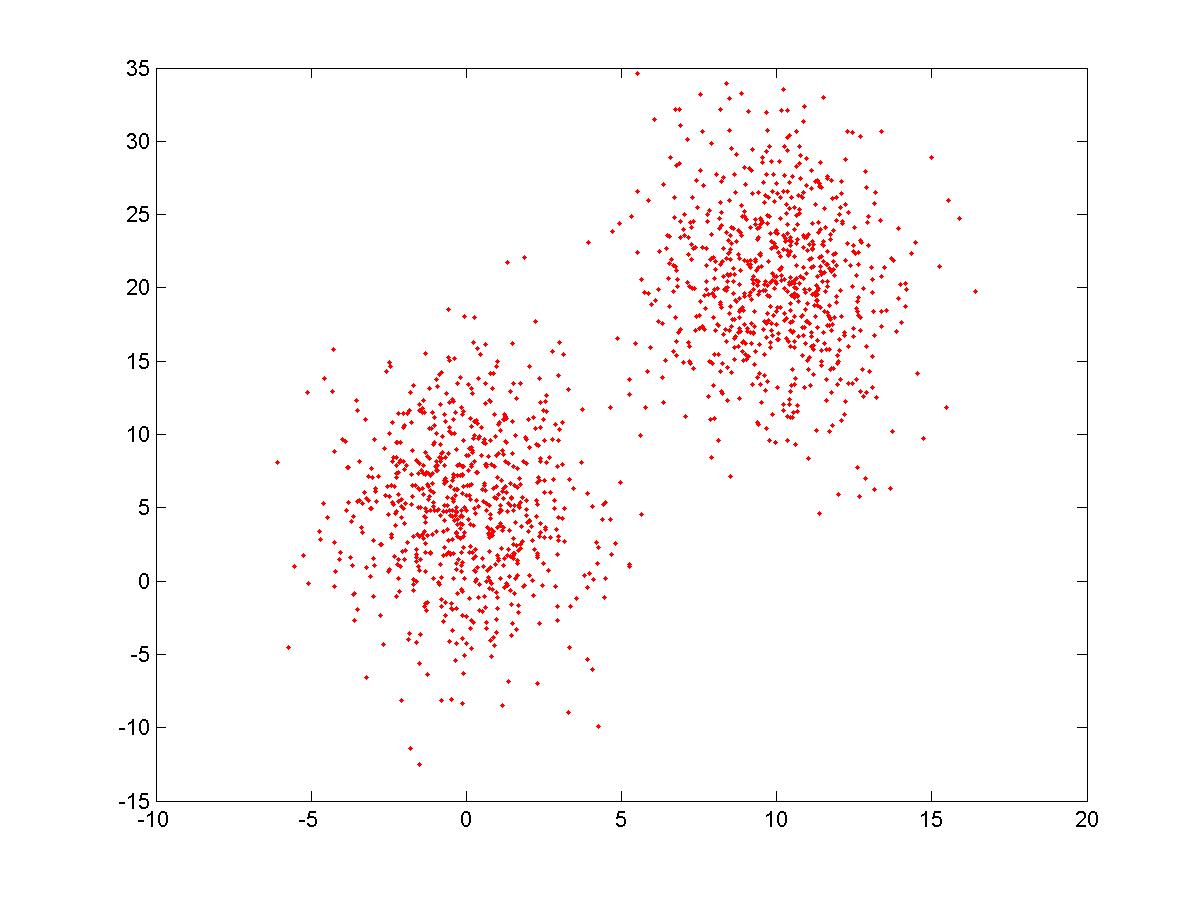
Рис.3. 2 кластера с центрами в (0,5) и (10,20)

Выделить в сформированной модели подмножество для обучения и тестирования в пропорции (2000 - обучение, 1000 - тест).

Варианты моделей (5 координат, 2 класса)

1. xi=[-10,10];

№ вар.	C1		C2
	D12	M1	D22	M2
1	0.3	[0,0,-1, 1, 2]	0.5	[-3, -3, 5, 1, 2]
2	0.5	[1,4,2, 1, 2]	0.4	[5, 5, -6, 1, 2]
3	0.1	[2, 0, 5, 3, 5]	0.3	[4, 3, 1, 3, 5]
4	0.5	[3, 2, 5, 3, 5]	0.2	[3, 6, 2, 3, 5]
5	0.1	[0,1,2, -2, -2]	0.4	[2, 3, -3, -2, -2]
6	0.2	[5, -1, 7, -2, -2]	0.5	[1, 7, 4, -2, -2]
7	0.1	[2, -2, -5, 3, 4]	0.5	[-1, -3, 6, 3, 4]
8	0.8	[3, -3, 4, 3, 4]	0.1	[-3, 3, 0, 3, 4]
9	0.1	[4, -4, 3, -1, 2]	0.2	[-2.3, -5, 2, -1, 2]
10	0.29	[0, -5, 1, -1, 2]	2.5	[-1, -5.3, -3, -1, 2]
11	0.1	[1, -6, -2, 3, 4]	0.5	[-1.3, 3.5, 4, 3, 4]
12	0.6	[2, -6, -5, 3, 4]	0.3	[2.5, -3.9, 5, 3, 4]

Сформировать 3 подмножества данных по признакам:

S1={x1, x2, x3, x4, x5};

S2={ x4, x5};

S3={x1, x2, x3}.