2.2. Виды и формы корреляционных связей.

Корреляционная связь между признаками может возникать различными путями.

Важнейший путь- причинная зависимость результативного признака Y (его вариации) от вариации факторного Х (регрессор) признака. Например, урожайность сельскохозяйственной культуры (Y) является результатом балла плодородности почвы (Х)- независимый фактор.

Корреляционная связь может возникнуть между двумя следствиями одной причины. Так классическим является пример, приведенный известным статистиком А.А.Чупровым. Если в качестве фактора Х взять число пожарных команд в городе, а за признак Y – сумму убытков в городе от пожаров, то между признаками Х и У обнаружится значительная прямая корреляция: в среднем, чем больше пожарных в городе, тем больше убытков от пожаров. Данную корреляционную связь нельзя интерпретировать, как связь причины и следствия, оба признака – следствия общей причины – размера города.

Современный пример. Сразу после 17 августа 1998 г. резко возросли цена валюты и объем ее покупки частными лицами. Здесь также нельзя рассматривать эти два явления как причину и следствие. Общая причина – обострение финансового кризиса, приведшие к росту курса валюты и стремление населения сохранить свои накопления в твердой валюте.

Такого рода корреляцию называют ложной.

Корреляция возникает и тогда, когда каждый из признаков и причина, и следствие.

Например, при сдельной оплате труда существует корреляция между производительностью труда и заработком.

По направлению выделяют связь прямую и обратную, по аналитическому выражению – прямолинейную и нелинейную. В данном учебном пособии мы будем рассматривать только линейную корреляционную зависимость.

В начальной стадии анализа статистических данных не всегда требуются количественные оценки, достаточно лишь определить направление и характер связи, выявить форму воздействия одних факторов на другие. Для этих целей применяются методы приведения параллельных данных, аналитических группировок и графический.

Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Например, сравним изменения двух величин:

Таблица 1

Х	1	2	3	4	5	6	7	8	9
У	5	9	6	10	12	17	15	20	23

С увеличением Х возрастает Y, поэтому связь между ними можно описать уравнением прямой.

Метод аналитических группировок характеризует качественного признака на относительные средние величины, на показатели вариации количественных признаков. В качестве группировочного признака выбирается факторный. В таблице размещают средние значения одного или нескольких признаков. Изменение факторного признака при переходе от одной группы к другой вызывают соответствующие изменения результативного признака.

Таблица 2.

№ группы	Среднее значение факторного признака Х	Среднее значение результативного признака У
1	2	6,6
2	5	13
3	8	19,3

Таблица ясно демонстрирует присутствие связи между признаками – это положительная связь, однако судить о том, линейная она или нет, по этим данным сложно.

Графический метод используется для наглядного изображения формы связи между изучаемыми признаками. Для этого на координатной плоскости строят точечный график, по оси абсцисс которой откладывают индивидуальные значения факторного признака, а по оси ординат – результативного. Совокупность точек факторного и результативного признаков называют полем корреляции.

Большинство методов измерения тесноты связи заключается в сопоставлении отклонений абсолютных значений величин от их средних. Они основаны на предположении о том, что при полной независимости переменных отклонение значения факторного признака от средней носят случайный характер и должны случайно сочетаться с различными отклонениями значений результативного признака.

Одну из первых попыток установления тесноты связи между переменными сделал Г. Фехнер, предложивший простейший показатель тесноты связи:

i =

Показатель Фехнера изменяется в промежутке . При значении равном 1, он указывает на положительную функциональную связь, при значении -1 – на отрицательную, при i=0 связь отсутствует. Промежуточные значения i характеризуют степень близости связи к функциональной.

Таблица 3

Х	1	2	3	4	5	6	7	8	9
У	5	9	6	10	12	17	15	20	23
Х-	-4	-5	-2	-1	0	1	2	3	4
У-	-8	-4	-7	-3	-1	4	2	7	10

Для данных таблицы 3. получены:

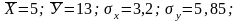
i= (9-1)/9=0,89.

Недостаток показателя Фехнера состоит в том, что разные по абсолютной величине отклонения имеют одинаковый вес.

Более совершенный измеритель связи между признаками – линейный коэффициент корреляции Пирсона (англ. статистик К.Пирсон). Он характеризует тесноту и направление связи между признаками в случае наличия между ними линейной зависимости. Смысл этого коэффициента более понятен, если его расчет производить с использованием коэффициента ковариации- это мера совместной вариации признаков.

С =

С помощью коэффициента ковариации можно определить наличие и направление связи. Однако его нельзя использовать для определения степени тесноты связи, так как он имеет смешанную размерность. Для преодоления этого недостатка можно это выражение разделить на средние квадратические отклонения по х и по у.

Полученный показатель интенсивности линейной связи называется коэффициентом корреляции:

r =

Эта безразмерная величина изменяется в интервале от -1 до 1.

Путем ряда преобразований можно получить другое аналитическое выражение коэффициента корреляции:

r =

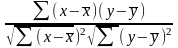
Линейный коэффициент корреляции имеет большое значение при исследовании социально-экономических процессов, распределения которых близки к нормальным.

Оценка достоверности коэффициента корреляции.

С уменьшением числа наблюдение надежность коэффициента корреляции падает, так как он является величиной случайной.

Определим доверительный интервал для оценки истинного значения коэффициента корреляции в генеральной совокупности ( :

r- t ,

где - среднеквадратическая ошибка выборочного коэффициента парной корреляции:

t – распределение Стьюдента с числом степеней свободы k= n-2 и уровнем значимости