Краевое государственное бюджетное образовательное учреждение среднего профессионального образования (среднее специальное учебное заведение)

«Красноярский техникум информатики и вычислительной техники»

УТВЕРЖДАЮ

Зам. директора по учебной работе

______________ Н.П. Бодрова

«_____»_____________ 2014г.

Учебное пособие для студентов заочного отделения

по учебной дисциплине

«Теория вероятности и математическая статистика»

специальности СПО 09.02.04 «Информационные системы (по отраслям»)

базовый уровень подготовки

Разработала: Пучкова О.В., преподаватель ВКК

Рассмотрено на заседании ЦК

«Образовательных дисциплин»

«___» ______________ 2014г.

Председатель____________ Н.Л.Овчаренко

Введение

Предмет и задачи дисциплины «Теория вероятности и математическая статистика».

Проявление закономерностей в экономике носит, как правило, статистический характер. Например, взаимосвязь спроса и цены товара на рынке, дефицита госбюджета и уровня инфляции, доходов населения и покупательской активности, уровня заработной платы и производительности труда. Если встаёт вопрос об увеличении налогов для покрытия социальных расходов, то необходимо проанализировать, как при этом изменяется уровень безработицы, темпы инфляции, рост НВП. Чтобы ответить на этот вопрос о взаимосвязи показателей – необходимо проанализировать ретроспективные данные.

В каждом конкретном случае экономические показатели рассматриваются, как отдельные случайные величины и может быть установлена их статистическая взаимосвязь.

Задача математической статистики – соединить на базе количественных измерений, теоретические и практические подходы к экономическим проблемам.

Раздел 1. Методы оценивания параметров статистических моделей.

1. Генеральная совокупность и выборка. Способы отбора.

Пусть изучается совокупность однородных объектов относительно некоторого количественного признака, характеризующего эти объекты. Например, доход населения, количество покупателей в магазине в течение дня, количество товаров в исследуемой партии и т.д.

Генеральной совокупностью называется множество всех возможных значений объектов одного вида при данном реальном комплексе условий.

Выборкой называется часть генеральной совокупности, отобранную для изучения.

Число элементов рассматриваемой совокупности называется её объёмом.

Изучение всей генеральной совокупности во многих случаях либо невозможно, либо нецелесообразно в силу больших материальных затрат, уничтожения или порчи исследуемых объектов. Например, анализ среднего дохода населения одного города формально предполагает наличие достоверной информации о каждом жителе города в данный момент времени. Получение такой информации просто невозможно. Проверка качества партии Абаканской тушенки связана со вскрытием банки, что приводит к невозможности её дальнейшей продажи. Поэтому на практике вся генеральная совокупность, практически никогда не анализируется. Для осуществления выводов о генеральной совокупности чаще всего используется выборка ограниченного объёма. В силу этого задача состоит в исследовании свойств выборки и обобщения этих свойств на всю генеральную совокупность. Полученный при этом вывод называется статистическим.

Информация о генеральной совокупности, полученная по выборке, обычно обладает некоторой погрешностью, так как она основывается только на части элементов выборки. Это определяет две проблемы:

• как организовать выборочное наблюдение, чтобы полученная информация достаточно полно отражала пропорции генеральной совокупности (проблема репрезентативности выборки)

• как использовать результаты выборки для суждения по ним с наибольшей надёжностью о свойствах и параметрах генеральной совокупности (проблема оценки)

В силу закона больших чисел можно утверждать, что выборка будет репрезентативной , если отбор будет носить случайный характер.

Различают повторную и бесповторную выборки. В первом случае отобранный объект перед отбором следующего возвращается в генеральную совокупность. Во втором- отобранный объект не возвращается в генеральную совокупность. Если выборка имеет малый объём, то различие между повторной и бесповторной выборкой стирается.

Случайный отбор может проводиться с помощью датчика таблицы случайных чисел или жеребьёвкой. Однако этот способ не всегда осуществим, так как требует чётко ограниченной базы статистического анализа, каковой является генеральная совокупность, перенумировки всех ее элементов и непосредственного их извлечения при жеребьевке. Поэтому прибегают к различным приемам неслучайного отбора.

Механический отбор, при котором элементы генеральной совокупности, предварительно упорядоченные , отбираются по заранее установленному правилу, не связанному с вариацией исследуемого признака. Например, можно фиксировать доход каждого сотого, входящего в метро.

Серийным называют отбор, при котором объекты выбираются из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Например, о продукции предприятия можно судить по продукции, выпущенной в какой-то конкретный день.

При типическом отборе объекты отбираются не из всей генеральной совокупности, а из каждой её «типической» части. Например, Население города можно предварительно классифицировать по социальному статусу (бизнесмены, чиновники, служащие, рабочие и т.д.). Нередко на практике применяется комбинированный отбор, при котором сочетаются описанные выше способы.

1.2 Способы представления и обработки статистических данных.

Во многих случаях для анализа тех или других экономических процессов важен порядок получения статистических данных. Задачей статистического описания выборки является получение такого ее представления, которое позволит наглядно выявить вероятностные характеристики. Для этого применяются различные формы упорядочения данных в выборке.

Построение дискретного вариационного ряда.

Задача 1.1. На телефонной станции проводились наблюдения над числом Х неисправных соединений в минуту в течение часа:

313114224030220214331

42211210341327200133

12420312511011221152

Произвести первичную обработку результатов наблюдений.

Построить эмпирическую функцию распределения и ее график.

Для решения задачи выполним следующие операции:

1. Ранжирование – операция, заключающаяся в том, что результаты наблюдений над СВ располагают в порядке неубывания:

0000001111111111111111122222222222222223333333333444444557

2. Установка варианта – значение СВ, соответствующее определенной группе наблюдаемых величин:

х₁= 0, х₂=1, х₃=2, х₄=3, х₅=4, х₆=5, х₇=7

3. Установить частоту варианта – количество элементов одного варианта:

m₁ =8, m ₂=17, m ₃=16, m ₄= 10, m ₅= 6, m ₆= 2, m ₇= 1

4. Установить относительную частоту варианта - отношение частоты варианта к количеству всех элементов выборки:

р₁ =8/60, р₂=17/60, р₃=16/60, р₄=10/60, р₅=6/60, р₆=2/60, р₇=1/60

5. Построить дискретный вариационный ряд – ранжированная совокупность значений СВ с соответствующими им частотами и относительными частотами:

Индекс	i	1	2	3	4	5	6	7
Вариант	хi	0	1	2	3	4	5	7
Частота	mi	8	16	17	10	6	2	1
Относительная частота	рi	8/60	16/60	17/60	10/60	6/60	2/60	1/60

6. Построить эмпирическую функцию распределения и ее график:

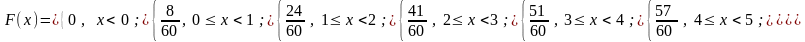
Наглядно вариационный ряд может быть представлен в виде полигона относительных

частот.

Дискретным вариационным рядом называется ранжированная совокупность

вариантов, соответствующих частот и относительных частот.

Построение интервального вариационного ряда.

Задача 1.2.. При измерении диаметра валиков после шлифовки получены следующие результаты:

6,75 6,77 6,77 6,73 6,76 6,74 6,70 6,75 6,71 6,72

6,73 6,70 6,73 6,77 6,75 6,74 6,71 6,70 6,78 6,76

6,77 6,69 6,74 6,70 6,70 6,74 6,77 6,83 6,76 6,76

6,77 6,75 6,74 6,75 6,77 6,72 6,74 6,80 6,75 6,80

6,78 6,78 6,76 6,77 6,74 6,74 6,77 6,73 6,74 6,77

Произвести первичную обработку результатов наблюдений. Построить эмпирическую функцию распределения и её график.

Для решения задачи выполним следующие операции:

1. Выбрать х_наим. = 6,69 и х_наиб.= 6,83;

2. Найти размах варьирования: R = х_наиб.-х_наим.= 6,83 – 6,69 = 0,14;

3. За число интервалов выбрать величину V = от 7 до 11;

4. Найти длину интервала h = = 0,02 ( V=7) ;

5. Вычислить х_{начальное}= х_наим. – 0,5h = 6,69- 0,01 = 6,68

х_{конечное} = х_наиб. + 0,5 h = 6,83 + 0,01= 6,84;

6. Построить интервальный вариационный ряд:

№	Интервал	Частота	Относительная частота
1	6,68 - 6,70	6	6/50
2	6,71 - 6,73	8	8/50
3	6,74 - 6,76	20	20/50
4	6,77 - 6,79	13	13/50
5	6,80 - 6,82	2	2/50
6	6,83 - 6,84	1	1/50

7. Построить эмпирическую функцию распределения и ее график:

Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами и относительными частотами ее попаданий в интервал.