Алгоритм вычисления обратной матрицы:

1. составить матрицу вида (А|Е_n).

1. привести в матрице (А|Е_n) подматрицу А к единичной матрице Е_n. При этом, подматрица Е_n, стоящая справа, будет приведена к матрице А^-1, т.е. получим матрицу (Е_n|А^-1).

Матричные уравнения.

Простейшие матричные уравнения имеют вид: 1) AX=B, 2) XA=B, 3) AXB=C, где А,В,С – некоторые матрицы.

Если А^-1, то в случае 1) X=A^-1B, в случае 2) X=BA^-1, в случае 3) XB=A^-1C. Если B^-1, то в случае 3) X=A^-1CB^-1.

4. Перестановки n-й степени. Определители n-го порядка.

Определение 1. Пусть М={1,2,…,n}. Перестановкой на множестве М или перестановкой n-й степени называется множество М с заданным расположением его элементов, и обозначается I=(i₁i₂…i_n), где i₁,i₂,..,i_n – попарно различные элементы из М.

Например, пусть М={1,2,3}. Тогда перестановки на М имеют вид: I₁=(132), I₂=(231), I₃=(123) и т.д.

Определение 2. Инверсией или беспорядком перестановки I называется любая пара символов перестановки I, в которой символ, стоящий левее, больше символа, стоящего правее.

Например, в перестановке I₂=(231) две инверсии: 31 и 21.

Через (I) обозначается число всех инверсий перестановки I.

Пример 1. Пусть I=(312465). Тогда перестановка I имеет три инверсии 31, 32, 65, т.е. (I)=3.

Определение 3. Перестановка I называется чётной, если (I) – чётное число, в противном случае перестановка I называется нечётной.

В примере 1 перестановка I – нечётная.

Через S_n обозначается множество всех перестановок n-ой степени.

Утверждение 1. | S_n |=n!.

Теорема 3 (теорема о чётности перестановки). Пусть в перестановке I на i-ом месте находится символ j. Если перестановка I₁ получена из перестановки I удалением символа j, то (-1) =(-1) ^+i+j .

Пусть А=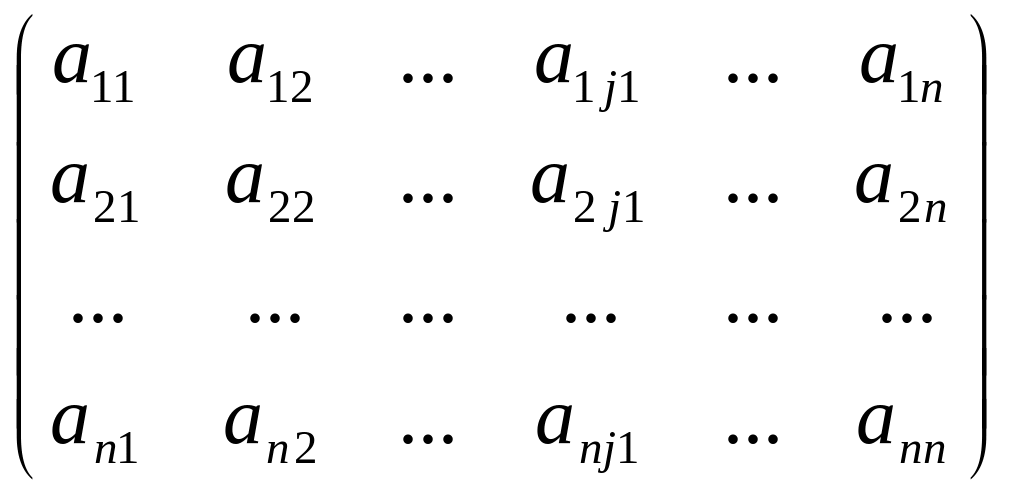 - матрица n-го порядка над полем Р.

Из элементов матрицы А будем составлять всевозможные произведения, состоящие из n множителей, любые два различных из которых находятся в разных строках и разных столбцах. Таким, например, является произведение элементов, стоящих на главной диагонали: a₁₁a₂₂…a_nn. Все такие произведения можно получить по следующему правилу: выберем для произведения из первой строки матрицы А некоторый элемент , затем вычеркнем первую строку и j₁-й столбец, и в полученной подматрице из первой строки выбираем некоторый элемент и т.д. Через конечное число шагов получим произведение вида: … .

Так как j₁,j₂,…,j_n – попарно различные элементы из множества М={1,2,…,n}, то вторые индексы в записанном произведении образуют перестановку I=(j₁j₂…j_n).

Рассмотрим выражение вида:

(-1) ^(I) , где I=(j₁j₂…j_n) (1).

Выражений вида (1) можно образовать столько, сколько существует перестановок, составленных из вторых индексов, т.е., ввиду утверждения 1, их будет n!.

Определение 4. Пусть А= - матрица над полем Р. Определителем матрицы А (или, коротко, определителем n-го порядка) называется элемент поля Р, равный

.

Используются следующие обозначения: =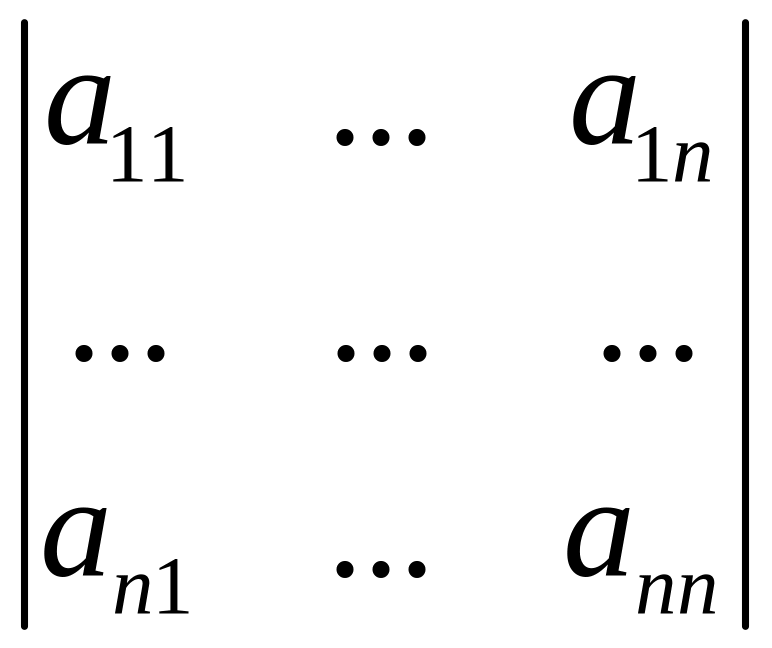 , =|A|, =|a_ij|, i= , j= , =det A.

5. Определители второго и третьего порядков.

1) Пусть Δ – определитель 2-го порядка, т.е., по определению 4 п.5, Δ = = .

M = , = 2! = 2. Таким образом, Δ имеет 2 слагаемых.

Выпишем все возможные 2 перестановки на множестве M = , подсчитаем количество инверсий в них и составим слагаемые вида (1) (см.п.5)

I₁ = (12) = 0 ,

I₂ = (21) = 1 , то

Δ = = .

Таким образом, определитель 2-го порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

2) Пусть Δ - определитель 3-го порядка: Δ = = .

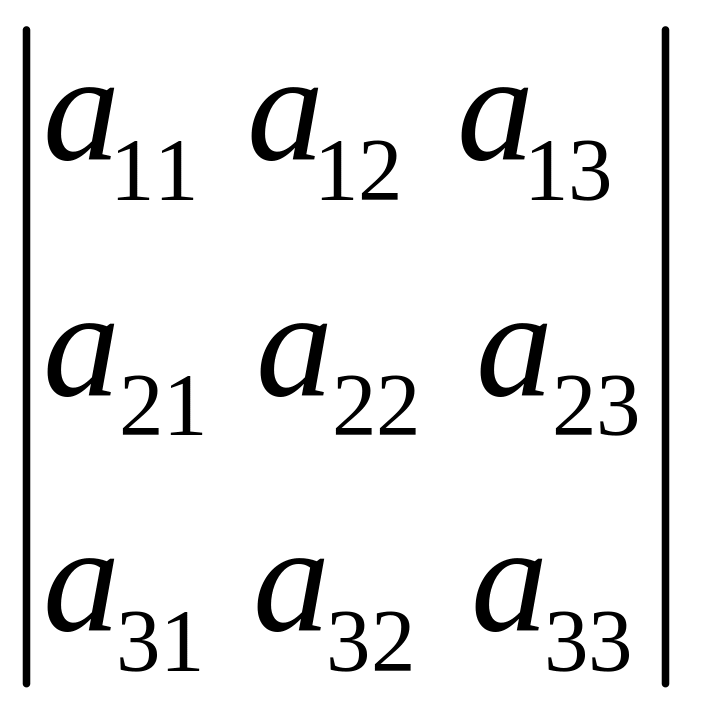M = , |S₃|= 3! = 6. Таким образом, Δ имеет 6 слагаемых.

Выпишем все возможные 6 перестановок на множестве M =

I₁ = (123) = 0 ;

I₂ = (213) = 1 ;

I₃ = (312) = 2 ;

I₄ = (321) = 3 ;

I₅ = (132) = 1 ;

I₆ = (231) = 2 .

Следовательно,

Δ= = .

Таким образом, определитель 3-го порядка равен сумме шести слагаемых, три из которых со знаком +:

произведение элементов на главной диагонали,

произведение элементов на диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу,

произведение элементов второй диагонали, параллельной главной, умноженное на элемент, стоящий в противоположном углу;

Остальные три слагаемых получают аналогично, только рассуждения проводят для побочной диагонали.

Записанное правило называют правилом Саррюса.