Глава 2. Математическая логика

2.1. Булевы функции.

Рассмотрим случай, когда элементами множества являются высказывания.

Высказывание есть любое повествовательное предложение, о котором можно сказать истинно оно или ложно. Высказывание является основным понятием математической логики. Широкое применение , кроме самой математики, раздел «Математическая логика» получил при анализе и синтезе логических схем входа и выхода данных в компьютерах и других цифровых устройствах.

Пример: «2x2=4» – истинное высказывание,

« Все студенты МГУКи владеют двумя языками» -- ложное высказывание,

« Да здравствует субботник» -- не высказывание.

Обозначают высказывания прописными буквами латинского алфавита x, y,z; истинностные значения – цифрами 0 (ложно) и 1(истинно).

Функции, аргументы и значения которых могут принимать только значения 0 и 1 называют булевыми функциями.

Операциями над высказываниями являются:

1. отрицание -- такое высказывание, которое истинно, когда x – ложно и наоборот.

-- отрицание (не x)

x
0	1
1	0

2. дизъюнкция (логическое сложение) – такое третье высказывание,

которое ложно в единственном случае: когда x и y оба ложны; в остальных случаях оно истинно.

-- дизъюнкция ( x или y)

x	y
1	1	1
1	0	1
0	1	1
0	0	0

3. конъюнкция (логическое умножение) – такое третье высказывание, которое истинно лишь в одном случае, когда x и y оба истинны, в остальных случаях – ложно.

-- конъюнкция (x и y)

x	y
1	1	1
1	0	0
0	1	0
0	0	0

4. импликация (логическое следствие) – такое третье высказывание, которое ложно в единственном случае, когда x—истинно, а y – ложно. В остальных случаях -- истинно.

-- импликация ( если x, то y)

x	y
1	1	1
1	0	0
0	1	1
0	0	1

5. эквиваленция (логическое равенство) – такое третье высказывание, которое истинно, когда x и y принимают одинаковые истинностные значения, в остальных случаях – ложно.

-- эквиваленция (тогда и только тогда)

x	y
1	1	1
1	0	0
0	1	0
0	0	1

Операции над высказываниями называют сентенциональными связями. С их помощью из элементарных высказываний можно получать сложные булевы функции (формулы). Порядок выполнения операций указывается скобками. Для упрощения записи принят ряд соглашений:

• для отрицания скобки опускаются ;

• имеет приоритет перед ;

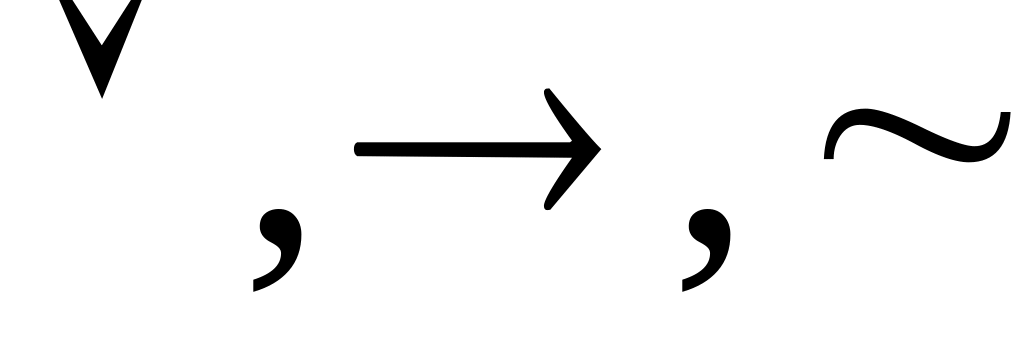• имеет приоритет .

Любая булева функция определяется своей таблицей истинности.

Пример: определим таблицу истинности булевой функции .

x	y
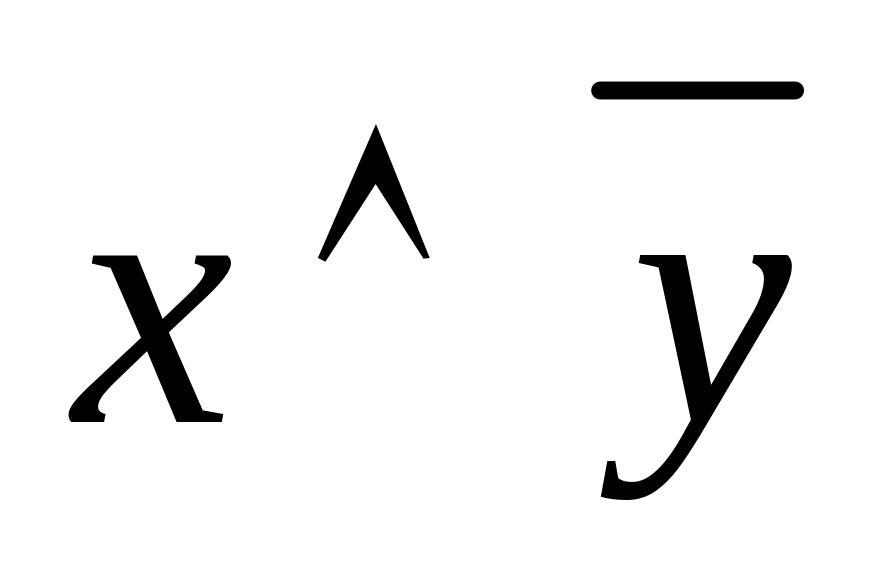
1	1	0	1	0	0	1
1	0	0	0	1	1	0
0	1	1	1	0	0	1
0	0	1	1	1	0	1

Две формулы алгебры высказываний равносильны, если они принимают одинаковые истинностные значения для всевозможных одинаковых истинностных значений в них входящих простых высказываний.

Пример: -- формула для исключения импликаций

Для установления равносильности формул, нужно составить таблицу истинности для левой и правой частей. Если истинностные значения совпадают, то формулы равносильны.

x	y
1	1	1	0	1
1	0	0	0	0
0	1	1	1	1
0	0	1	1	1

В алгебре высказываний имеют место следующие основные равносильности:

Замечание: заменив в формулах множества на высказывания, , получим, что законы алгебры множеств перейдут в законы алгебры высказываний; т.е. две алгебры отличаются лишь по форме входящих в них элементов. Алгебраически они неразличимы (изоморфны).

Если формула для любых значений истинности элементарных высказываний принимают только значения истинно(ложно), то она называется тождественно-истинной(тождественно-ложной) функцией.

т.и.(т.л) – тавтологии – 1(0)

Любая тавтология выражает собой некоторый логический закон.

Пример: -- закон отделения

x	y
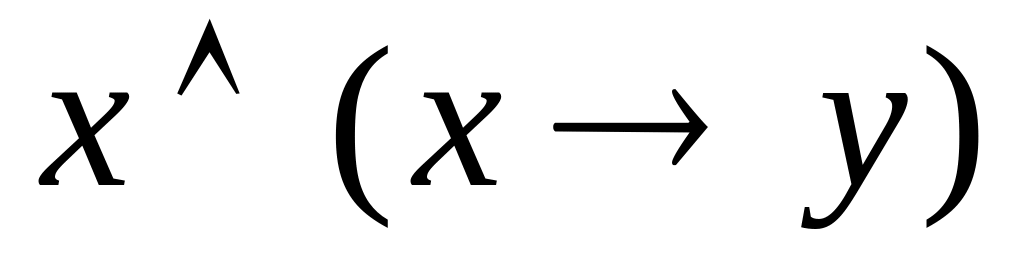
1	1	1	1	1
1	0	0	0	1
0	1	1	0	1
0	0	1	0	1

Число булевых функций от n переменных равно .

Пример: если n=1, то ;

Если n=2, то . Все они указаны в таблице:

0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

У некоторых из этих функций есть специальные названия.

-- тождественный нуль.

-- конъюнкция. Часто знак не пишут ( )

-- сложение по модулю 2.

-- дизъюнкция.

-- стрелка Пирса.

-- эквивалентность.

-- импликация.

-- штрих Шеффера.

-- тождественная единица.

Часто при задании булевой функции ограничиваются указанием ее набора значений. Например, .

Задачи.

1. Предположим, что высказываниям x, y, z и t соответствуют значения 1, 0, 0 и 1. Найти истинностные значения каждого из следующих высказываний:

a) ;

b) ;

c) ;

d) .

2. Пусть значение высказывания

a) истинно;

b) ложно.

Что можно сказать о значениях высказываний и ?

3. С помощью таблицы истинности доказать формулы:

а) -- исключение импликации;

b) -- исключение эквивалентности: .

4. С помощью таблицы истинности доказать законы:

a) -- закон силлогизма;

b) -- закон отделения;

c) -- закон контрапозиции.