Дискретная математика
Введение
Дискретная математика – это раздел математики, который опирается на понятие дискретного – прерывного множества. К этому разделу относятся элементы теории конечных множеств как фундамента дискретной математики, теория графов как наглядное представление дискретных множеств, имеющую широкое применение комбинаторику, элементы математической логики, включающие булеву алгебру и алгебру высказываний.
Данное пособие предназначено для студентов дневного и заочного отделений, обучающихся по специальности « Прикладная информатика». Включает в себя курс лекций по основным разделам дискретной математики: множества, математическая логика, комбинаторика и теория графов. Каждая лекция содержит примеры и заканчивается упражнениями, с помощью которых студент может определить уровень понимания данного материала.
Содержание
Глава 1. Элементы теории множеств.
Множества
Отношения
Отображения. Функции
Глава 2. Математическая логика.
2.1. Булевы функции
2.2. Нормальные формы
2.3. Минимизация нормальных форм
2.4. Контактные схемы
2.5. Логика предикатов
2.6. Решение логических задач с помощью булевых функций
Глава 3. Комбинаторика.
3.1. Общие правила комбинаторики
3.2. Перестановки
3.3. Размещения
3.4. Сочетания
Глава 4. Элементы теории графов.
4.1. Основные понятия теории графов.
4.2. Задача определения кратчайшего пути.
4.3. Задача о кратчайшем расстоянии между двумя пунктами.
4.4. Построение коммуникационной сети минимальной длины.
4.5. Задача определения максимального потока.
Глава 1. Элементы теории множеств.
1.1. Множества.
Теория множеств как математическая дисциплина создана немецким математиком Г.Кантором (1845-1918).
Множество – одно из основных (фундаментальных) понятий математики, а потому строгого определения не имеет. Описательно термин «множество» объясняется как собрание, совокупность, набор некоторых объектов произвольной природы, объединенных по каким-то общим для них признакам. Объекты, из которых состоит множество, называют его элементами.
Примеры множеств: все студенты университета, собрание книг в библиотеке, множество звезд Солнечной галактики, множество целых чисел и т.д.
Исходя из примеров, можно определить свойства множества:
1) элементы множества должны быть строго определены;
2) каждый элемент должен учитываться только один раз;
3) порядок расположения элементов внутри множества не имеет значения.
Пример: Множество студентов какой-либо группы университета.
Понятно, принадлежит студент данной группе или нет, в ведомости каждый учитывается только раз и порядок расположения фамилий не имеет значения.
Множества обозначают заглавными буквами латинского алфавита: A, B, C, D ...; элементы – строчными: a, b, c, ...
Символическая запись
означает принадлежность элемента a
множеству А. Запись
означает,
что элемент а не принадлежит множеству
А.
Пример: Пусть А – множество четных
чисел. Тогда
,
а
.
Если число элементов множества конечно, то множество называют конечным, иначе – бесконечным. Считается, что примеры множеств, взятых из материального мира, конечны. Числовые множества – бесконечны.
Пример: Множество рыб в океане велико, но конечно. Множество действительных чисел – бесконечно.
Множество, не содержащее ни одного
элемента, называется пустым и обозначается
символом
.
Существуют разные способы задания множеств. Конечное множество можно задать перечислением его элементов.
Пример: С=
--
множество цифр десятичной системы
счисления.
Также задать множество можно с помощью характеристического признака.
Пример:
--
множество четных чисел.
Два множества равны, когда они состоят из одних и тех же элементов.
Пример: Множества
и
равны.
Пример: Множества
и
равны.
Множество А называют подмножеством
множества В, если каждый элемент множества
А является одновременно элементом
множества В. В этом случае пишут
(читается: «А включается или содержится
в В»). Любое множество содержит
в
качестве подмножества. Очевидно,
(
записывают
);
А и
называют
несобственными подмножествами множества
А. Все остальные подмножества называют
собственными, т.е. кроме его элементов
в множестве должен содержаться еще хотя
бы один элемент.
Пример: Пусть
,
тогда
.
Основные свойства включения: если
;
если
--
равные множества.
Если все рассматриваемые множества, в ходе какого-либо рассуждения, являются подмножествами некоторого множества U, то это множество называют универсальным.
Пример: R – множество действительных чисел – универсальное множество, если в процессе изучения рассматриваются множества натуральных, целых и рациональных чисел
Существуют следующие операции над множествами:
объединение:
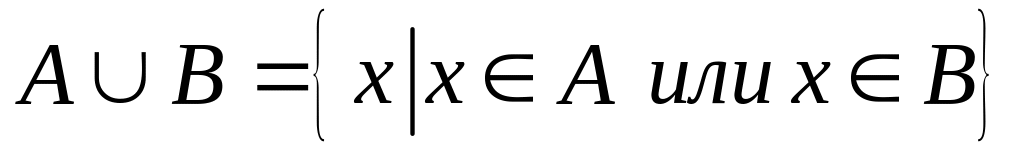-- элементы нового множества лежат хотя
бы в одном из множеств А или В;пересечение:
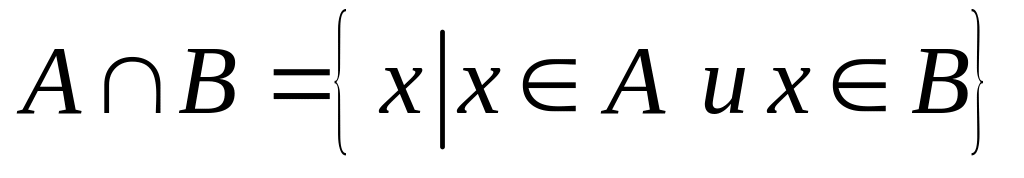-- элементы нового множества лежат в
обоих множествах А; В;разность:
-- элементы нового множества – это
элементы множества А, не содержащиеся
в В;дополнение множества А в множестве U (
):
.
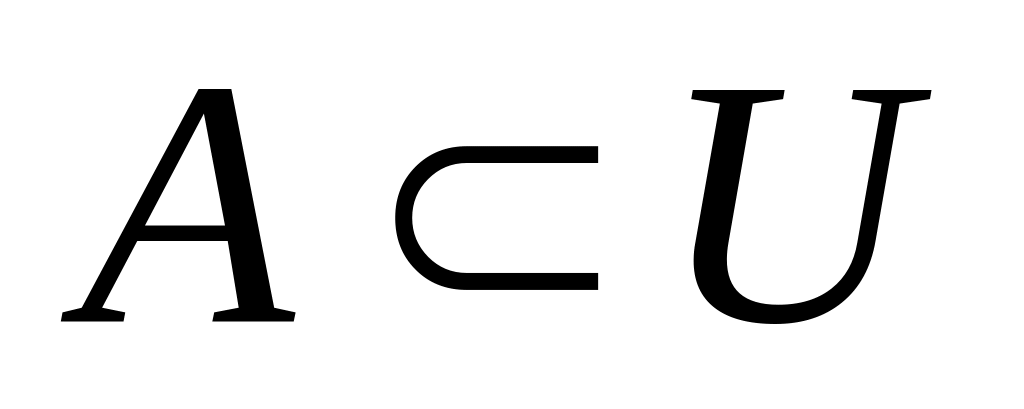Пример:
.
Тогда
.
Введенные операции обладают следующими свойствами:
(коммутативность).
(ассоциативность).
(дистрибутивность)
(идемпотентность).
(поглощение).
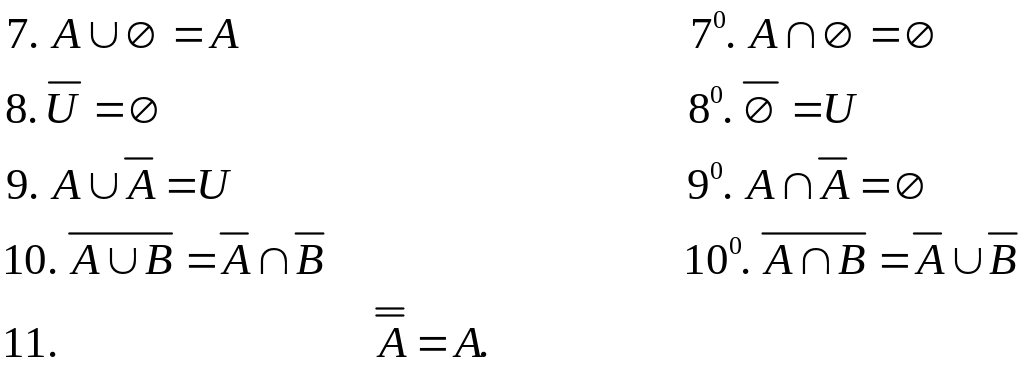
Задачи.
Используя диаграмму Венна, доказать законы 3 и 5.
Используя законы множеств, доказать равенства:
a)
.
b)
.
c)
.
3. Заданы множества
.
Верным для них будет утверждение...
Варианты ответов:
a) «Множества А и В равны».
b) «Множество B есть подмножество множества A».
c) «Множество А есть подмножество множества В».
d) «Множества А и В не содержат одинаковых элементов».
4. Заданы произвольные множества А, В и С. Расположить указанные ниже четыре множества так, чтобы каждое из них было подмножеством следующего за ним:
a)
b)
c)
d)
.
5. Даны множества
.
Установить соответствия между следующими
множествами и их элементами:
6. Принято обозначать:
N – множество натуральных чисел;
Q – множество рациональных чисел;
Z – множество целых чисел;
R – множество действительных чисел.
Тогда верным утверждением будет...
Варианты ответов:
7. С помощью диаграмм Венна исследовать вопрос о справедливости каждого из следующих рассуждений:
а) если А, В, и С – такие подмножества множества U, что
;
b) если А, В, и С –
такие подмножества множества U,
что
и
,
то
.