
Содержание.
1. Задача 1…………………………………………….…………………………….3
2. Задача 2…………………………………………………………………………..7
3.Задача 3……………………………………………………………………..……8
4. Задача 4………………………………………………..………………….…......10
5. Задача 5 ……………………………………………………………………...….11
6.Задача 6…………………………………………………………………………..12
7.Задача 7………………………………………………………………………..…13
4.Список литературы………………………..……………………………….........15
Задача 1.
По ряду предприятий имеются следующие данные:
Номер п/п |
Валовая продукция, млн.руб. |
Среднесписочное число работающих |
Среднегодовая стоимость основных производственных фондов, млн.руб |
Прибыль, тыс.руб. |
1 |
360 |
145 |
390 |
23 |
2 |
480 |
219 |
470 |
46 |
3 |
980 |
519 |
1590 |
76 |
4 |
230 |
132 |
240 |
17 |
5 |
1330 |
338 |
1240 |
88 |
6 |
490 |
238 |
680 |
32 |
7 |
780 |
344 |
760 |
58 |
8 |
760 |
206 |
590 |
4 |
9 |
960 |
402 |
900 |
74 |
10 |
920 |
495 |
1180 |
67 |
11 |
340 |
201 |
740 |
30 |
12 |
1300 |
530 |
120 |
93 |
13 |
1550 |
355 |
480 |
109 |
14 |
130 |
140 |
250 |
10 |
15 |
1840 |
98 |
180 |
12 |
16 |
1360 |
35 |
1030 |
40 |
На основе выше представленных результатов 15 % выборочного обследования ТЭП деятельности предприятий города следует :
1) По исходным данным таблицы № 1 произвести группировку предприятий по размеру товарооборота предприятия, выделив 4 групп. Методом аналитической группировки установить характер тесноты связи между исходными ТЭП на одно предприятие с помощью показателей средних величин и оценить структуру распределения предприятий по группам. Результаты оформить в виде таблицы. Сделать выводы.
2) С вероятностью 95,4% установить доверительный интервал среднего уровня группировочного признака для всех предприятий региона. Сделать выводы.
РЕШЕНИЕ
Упорядочим предприятия по размеру валовой продукции:
Таблица 2 – Показатели по возрастанию валовой продукции
Номер п/п |
Валовая продукция, млн.руб. |
Среднесписочное число работающих |
Среднегодовая стоимость основных производственных фондов, млн.руб |
Прибыль, тыс.руб. |
14 |
130 |
140 |
250 |
10 |
4 |
230 |
132 |
240 |
17 |
11 |
340 |
201 |
740 |
30 |
1 |
360 |
145 |
390 |
23 |
2 |
480 |
219 |
470 |
46 |
6 |
490 |
238 |
680 |
32 |
8 |
760 |
206 |
590 |
4 |
7 |
780 |
344 |
760 |
58 |
10 |
920 |
495 |
1180 |
67 |
9 |
960 |
402 |
900 |
74 |
3 |
980 |
519 |
1590 |
76 |
12 |
1300 |
530 |
120 |
93 |
5 |
1330 |
338 |
1240 |
88 |
16 |
1360 |
35 |
1030 |
40 |
13 |
1550 |
355 |
480 |
109 |
15 |
1840 |
98 |
180 |
12 |
Определим ширину интервала:
 тыс. руб.
тыс. руб.
Так как ширина интервала округлялась, то границу первого интервала примем 125 тыс. руб., а последнего 1845 тыс. руб.
Представим результаты группировки в таблице:
Таблица 3 - Анализ структуры ТЭП деятельности предприятий города
№ интервала |
Группировка по валовой продукции, млн. руб. |
Коли-чество предп-риятий |
Валовая продукция |
Среднеспи-сочное число работающих |
Стоимость ОФ |
Прибыль |
||||
всего, млн. руб. |
% к итогу |
всего, чел |
% к итогу |
всего, млн. руб |
% к итогу |
всего, тыс. руб |
% к итогу |
|||
1 |
125-555 |
6 |
2030 |
14,70 |
1075 |
24,45 |
2770 |
25,55 |
158 |
20,28 |
2 |
555-985 |
5 |
4400 |
31,86 |
1966 |
44,71 |
5020 |
46,31 |
279 |
35,82 |
3 |
985-1415 |
3 |
3990 |
28,89 |
903 |
20,54 |
2390 |
22,05 |
221 |
28,37 |
4 |
1415-1845 |
2 |
3390 |
24,55 |
453 |
10,30 |
660 |
6,09 |
121 |
15,53 |
Итого |
|
16 |
13810 |
100 |
4397 |
100 |
10840 |
100 |
779 |
100 |
Между количеством попадания предприятий в группу и удельными весами ТЭП деятельности предприятий города существует прямая зависимость. Зависимость нарушается только для первой группы: число предприятий в ней наибольшее, а удельный вес показателей ТЭП не максимальный. Однако для все остальных групп при уменьшении числа предприятий в группе уменьшается и удельный вес показателя в общем итоге.
Методом аналитической группировки установить характер тесноты связи между исходными ТЭП на одно предприятие с помощью показателей средних величин. Рассчитаем средние показатели на одно предприятие, а так же рентабельность продукции, основных фондов и прибыль на одного работника
Таблица 4-Аналитическая группировка предприятий по уровням рентабельности производства
№ интервала |
Группи-ровка по валовой продукции, млн. руб. |
Коли-чество предп-риятий |
Зависимость рентабельности от группировочного признака |
Средние ТЭП деятельности на одно предприятие города |
||||||
Рента-бельность ОФ |
Рента-бельность продукции |
Прибыль на одного работника, тыс. руб. |
Валовая продук-ция, млн. руб. |
Среднее число работ-ников |
Средняя стоимость ОФ, млн. руб. |
Средняя прибыль, млн. руб. |
||||
1 |
125-555 |
6 |
5,70 |
7,78 |
0,147 |
338,3 |
179,2 |
461,7 |
26,3 |
|
2 |
555-985 |
5 |
5,56 |
6,34 |
0,142 |
880,0 |
393,2 |
1004,0 |
55,8 |
|
3 |
985-1415 |
3 |
9,25 |
5,54 |
0,245 |
1330,0 |
301,0 |
796,7 |
73,7 |
|
4 |
1415-1845 |
2 |
18,33 |
3,57 |
0,267 |
1695,0 |
226,5 |
330,0 |
60,5 |
|
Как видно из данной таблицы при увеличении выпуска продукции увеличивается рентабельность основных фондов, прибыль на одного работники и средняя прибыль. Рентабельность продукции при этом уменьшается.
С вероятностью 95,4% установим доверительный интервал среднего уровня группировочного признака для всех предприятий региона
Таблица 5 – Расчет выборочной средней и дисперсии
№ интервала |
Группировка по валовой продукции, млн. руб. |
Середина интервала хi |
Кол-во предп-риятий ni |
xini |
(xi- |
1 |
125-555 |
340 |
6 |
2040 |
1252408,59 |
2 |
555-985 |
770 |
5 |
3850 |
3611,32813 |
3 |
985-1415 |
1200 |
3 |
3600 |
487529,297 |
4 |
1415-1845 |
1630 |
2 |
3260 |
1388194,53 |
Итого |
|
|
16 |
12750 |
3131743,75 |
Выборочная средняя
 =796,875
млн. руб.
=796,875
млн. руб.
выборочная дисперсия
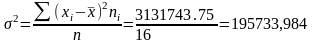
Предельная ошибка для среднего значения при бесповторной выборке определяется по формуле:
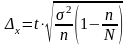
n =16 – численность выборки
N– размер генеральной совокупности
отношение
 показывает процент отбора, то есть в
данном случае
=0,15
показывает процент отбора, то есть в
данном случае
=0,15
t – коэффициент доверия, определяемый по таблице значений функции Лапласа. При вероятности равной 0,954 коэффициент доверия составляет t =2. Значит, предельная ошибка, выборки примет значение
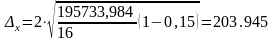 млн.
руб.
млн.
руб.
Доверительный интервал средней находится в границах
![]() =[
=[![]() в-x;
в
+x]
в-x;
в
+x]
= [796,875-203,945; 796,875+203,945]= [592,93; 1000,82].
Таким образом, с вероятностью 0,954 можно гарантировать, что средний размер валовой продукции по всем предприятиям города не будет меньше 592,93 млн. руб. и не превысит 1000,82 млн. руб.
Задача 2.
Имеются данные о дальности перевозок и грузообороте 5 грузовых автомашин за день.
№ грузового автомобиля |
Дальность перевозки 1 т груза, км |
Грузооборот, тонно-км |
№ 1 |
7 |
70 |
№2 |
5 |
50 |
№3 |
16 |
460 |
№4 |
8 |
140 |
№5 |
9 |
65 |
Определить среднюю дальность перевозки 1 тонны груза и уровень вариации между подвижным составом.
РЕШЕНИЕ
Среднюю дальность перевозки грузов определяют делением грузооборота (в т-км) на количество перевезённых тонн.
Для расчета данного показателя преобразуем ряд к виду:
№ грузового автомобиля |
Дальность перевозки 1 т груза, хi км |
Количество перевезенных тонн груза ni |
№ 1 |
7 |
70/7=10 |
№2 |
5 |
50/5=10 |
№3 |
16 |
460/16=28,75 |
№4 |
8 |
140/8=17,5 |
№5 |
9 |
65/9=7,22 |
Рассчитаем среднюю дальность перевозки и показатели вариации:
Таблица 6 – Расчет показателей вариации
№ п/п |
xi |
ni |
xini |
(xi- )2ni |
1 |
7 |
10 |
70 |
135,74 |
2 |
5 |
10 |
50 |
323,11 |
3 |
16 |
28,75 |
460 |
812,38 |
4 |
8 |
17,5 |
140 |
126,10 |
5 |
9 |
7,22 |
65 |
20,49 |
ИТОГО |
|
73,47 |
785,00 |
1417,82 |
Средняя дальность перевозки:
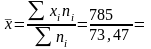 10,684
км
10,684
км
Дисперсия:
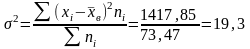
Среднее
квадратическое отклонение:
 4,393
км
4,393
км
Коэффициент
вариации:
 100=41,1%
100=41,1%
Таким образом, в среднем дальность перевозки составляла 10 км 84 м. Подвижной состав неоднороден, отличается значительной вариацией.
Задача 3.
В целях контроля за соблюдением норм расхода сырья проведено выборочное обследование партии готовой продукции. При механическом способе отбора 2% изделий получены следующие данные о весе обследованных единиц:
Вес изделия, гр |
Число образцов, шт |
до 2000 |
8 |
от 2000 до 2050 |
43 |
от 2050 до 2100 |
29 |
от 2100 до 2150 |
10 |
свыше 2150 |
2 |
При условии, что к стандартной продукции относятся изделия с весом от 2000 до 2150 г., установите для всей партии:
1) с вероятностью 0.954 возможны пределы удельного веса стандартной продукции;
2) с вероятность 0.997 возможные пределы среднего веса одного изделия в генеральной совокупности.
РЕШЕНИЕ
Для вычисления генеральных значений вычислим выборочную среднюю и выборочную дисперсию. При этом первый и последний интервал преобразуем в закрытые, приняв их длины равными 50 гр.
Таблица 7 – Расчет выборочных характеристик
№ интервала |
Вес изделия, гр |
Середина интервала хi |
Число образцов, шт ni |
xini |
(xi- )2ni |
1 |
1950-2000 |
1975 |
8 |
15800 |
45654,54 |
2 |
2000-2050 |
2025 |
43 |
87075 |
28056,18 |
3 |
2050- 2100 |
2075 |
29 |
60175 |
17345,52 |
4 |
2100-2150 |
2125 |
10 |
21250 |
55437,74 |
5 |
2150-2200 |
2175 |
2 |
4350 |
30978,85 |
Итого |
|
|
92 |
188650 |
177472,83 |
Выборочная средняя:
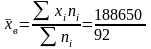 =2050,543
г
=2050,543
г
Дисперсия:

1) Доля продукции весом 2000-2150 г. в выборке =(43+29+10)/92=0.8913
При вероятности равной 0,997 коэффициент доверия составляет t =3.
Предельная ошибка доли:
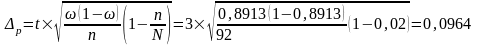
Получаем интервал: (0,8913-0,0964; 0,8913+0,0964)=( 0,7949; 0,9873) – с вероятностью 0,9997 доля стандартной продукции составит от 79,49% до 98,73%.
2) Определим пределы для средней
 г.
г.
Доверительный интервал средней находится в границах
= [2050,543-9,066; 2050,543+9,066]= [2041,477; 2059,609].
Таким образом, с вероятностью 0,954 можно гарантировать, что средний вес изделия в генеральной совокупности не будет меньше 2041,477 г. и не превысит 2059,609 г.

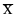 )2ni
)2ni