§ 1.3.4. Независимые события. Теорема умножения для независимых событий
Пусть вероятность события не зависит от появления события .
Событие называют независимым от события , если появление события не изменят вероятности события , то есть если условная вероятность события равна его безусловной вероятности:
.
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противоположном случае события называют зависимыми.
Теорема умножения для независимых событий. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
.
Пример 1.29.
Найти вероятность совместного поражения
цели двумя орудиями, если вероятность
поражения цели первым орудием (событие
)
,
а вторым (событие
)
.
Решение. и независимые, поэтому по теореме умножения
.
Несколько событий называют попарно независимыми, если каждые два из них независимы.
Следствие теоремы умножения. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
.
Пример 1.30.
Вероятности появления каждого из 3-х
независимых событий
,
соответственно, равны
.
Найти вероятность появления только одного из этих событий.
Решение.
Пусть событие
– появление только
,
что равносильно
;
событие
– появление только
,
что равносильно
;
событие
– появление только
,
что равносильно
.
События
– несовместные, следовательно:
.
Так как независимые, то
,
,
.
Таким образом,
.
§ 1.3.5. Вероятность появления хотя бы одного события
Пусть в результате испытания могут появиться “ ” событий. Как найти вероятность того, что наступит хотя бы одно из этих событий?
Теорема.
Вероятность появления хотя бы одного
из событий
,
,…,
,
независимых в совокупности, равна
разности между единицей и произведением
вероятностей противоположных событий
,
,…
:
.
Пример 1.31.
Вероятности попадания в цель при стрельбе
из трех орудий таковы:
;
;
.
Найти вероятность хотя бы одного попадания (событие ) при одном залпе из всех орудий.
Решение. Пусть событие – попадание 1-го орудия,
событие – попадание 2-го орудия, событие – попадание 3-го орудия.
, и – независимые в совокупности.
Вероятность события
.
Тогда 
.
§ 1.3.6. Вероятность гипотез. Формулы Бейеса
Пусть событие
может наступить при условии появления
одного из несовместных событий
,
образующих полную группу.
Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами.
Вероятность появления события определяется по формуле полной вероятности:
.
Допустим, что произведено испытание, в результате которого появилось событие . Будем искать условные вероятности:
.
Найдем сначала
условную вероятность
.
По теореме умножения вероятностей имеем
.
Тогда
.
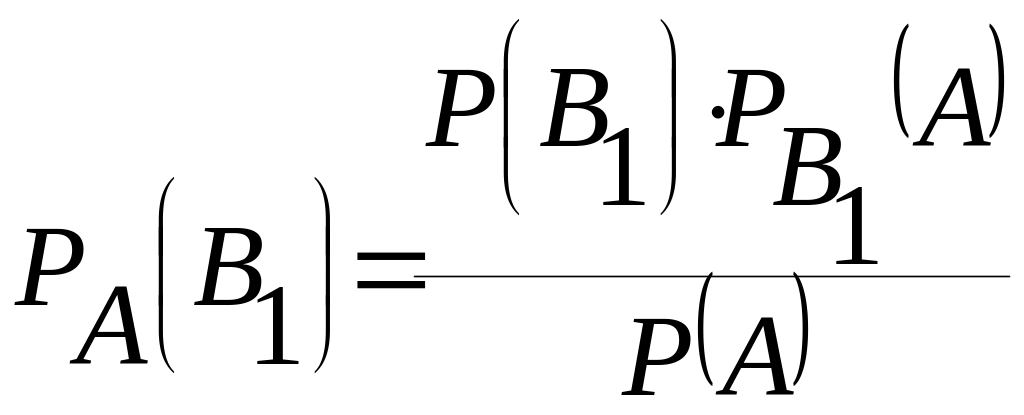Так как
Тогда
.
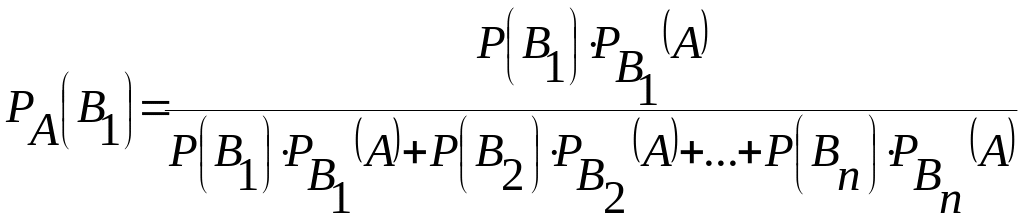Аналогично
выводятся формулы, определяющие условные
вероятности остальных гипотез, то есть
условная вероятность любой гипотезы
(
)
может быть вычислена по формуле
.
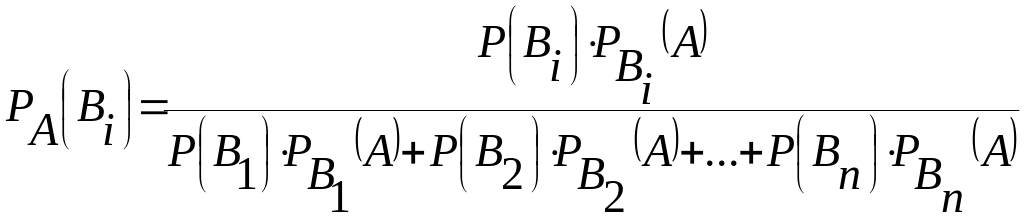Пример 1.32. Экзамен проводится двумя экзаменаторами. Вероятность того, что студент попадет к первому экзаменатору равна 0,65, а ко второму – 0,35.
Вероятность того, что студент сдаст экзамен, попав к первому экзаменатору равна 0,85, а вероятность того, что студент сдаст экзамен, попав ко второму экзаменатору – 0,7.
Студент сдал экзамен.
Найти вероятность того, что студент сдавал экзамен первому экзаменатору.
Решение. Обозначим через событие, состоящее в том, что студент сдал экзамен.
Пусть гипотеза
состоит в том, что студент сдавал первому
экзаменатору, а
– что студент сдавал второму.
Искомую вероятность найдем по формуле Бейеса:
.
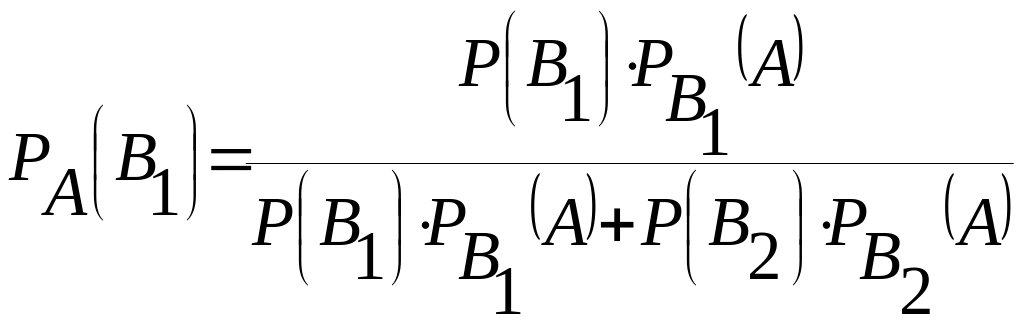Из условия задачи следует, что
.
Тогда
.
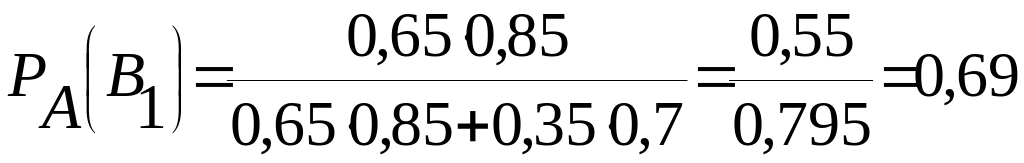