§ 1.2. Теорема сложения вероятностей § 1.2.1. Теорема сложения вероятностей несовместных событий

Суммой двух событий и называют событие, состоящее в появление события , или события , или обоих этих событий.

Например, если из орудия произведены 2 выстрела и событие означает попадание при первом выстреле, событие – попадание при втором выстреле, то – попадание при 1-м выстреле или при 2-м.

В частности, если два события и – несовместные, то - событие, состоящее из появления одного из этих событий, безразлично какого.

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.

Например, событие состоит в появлении одного из следующих событий: ; ; ; и и ; и ; и и .

Пусть события и – несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо , либо событие?

Теорема сложения

Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий.

.

Следствие

Вероятность появления одного события из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий.

.

Пример 1.21. В урне 30 шаров: 10 шаров красного цвета, 5 – синего и 15 белого. Вытаскивают один шар.

Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает, что вытащенный шар либо красного цвета, либо синего. Вероятность появления красного шара равна

.

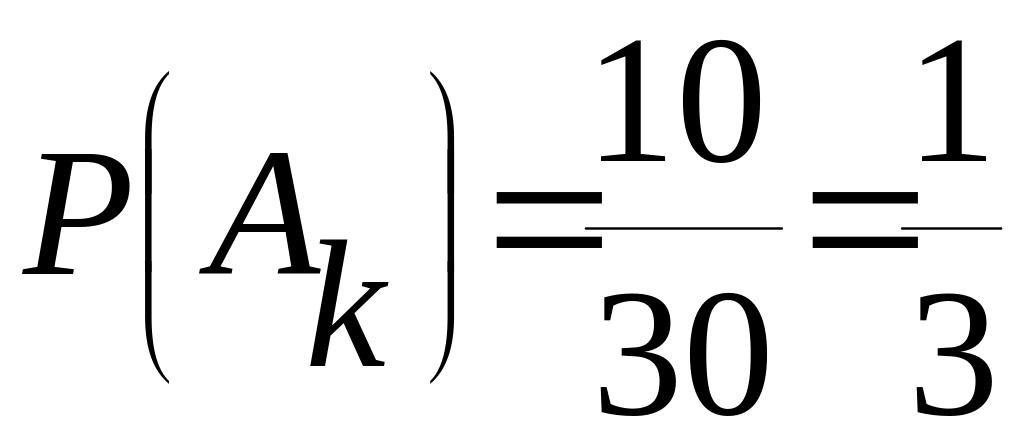Вероятность появления синего шара равна .

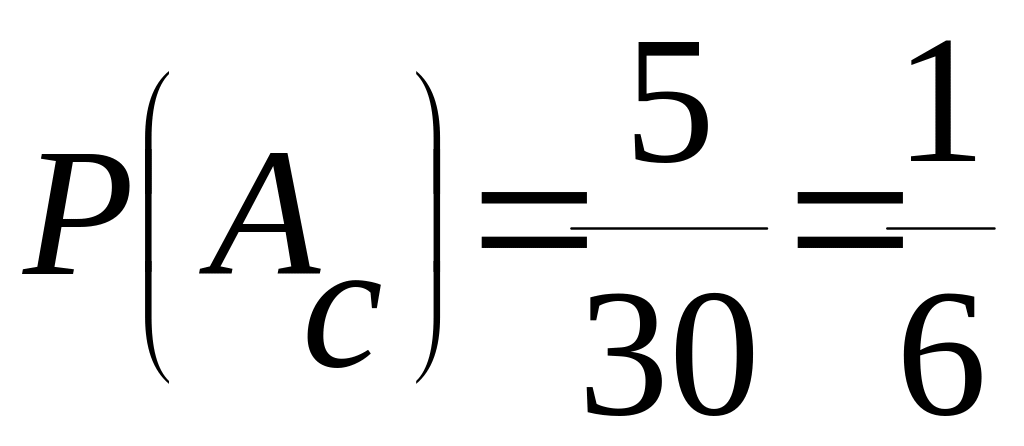Так как и - несовместные события (появление красного исключает появление синего), то

.

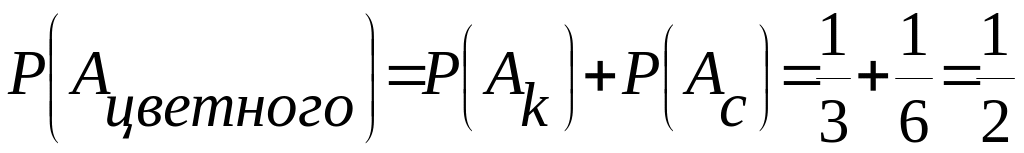Пример 1.22. Стрелок стреляет по мишени, разделенной на 3 области.

Вероятность попадания в первую область равна , вероятность попадания во вторую область равна .

Найти вероятность того, что стрелок при одном выстреле попадет либо в первую, либо во вторую область.

Решение. Пусть событие – попадание в первую область, событие – попадание во вторую область. Это два несовместных события, тогда

.

Пример. 1.23. На стеллаже библиотеки в случайном порядке расставлено 15 учебников. Причем 5 из них - в жестком переплете. Библиотекарь берет наудачу три учебника.

Найти вероятность того, что хотя бы один из взятых учебников окажется в жёстком переплёте.

Решение. Пусть событие – один учебник в жестком переплете, событие – два учебника в жестком переплете, событие – три учебника в жестком переплете. Тогда вероятность события (хотя бы один из взятых учебников окажется в жестком переплете) равно . Вычислим:

,

,

,

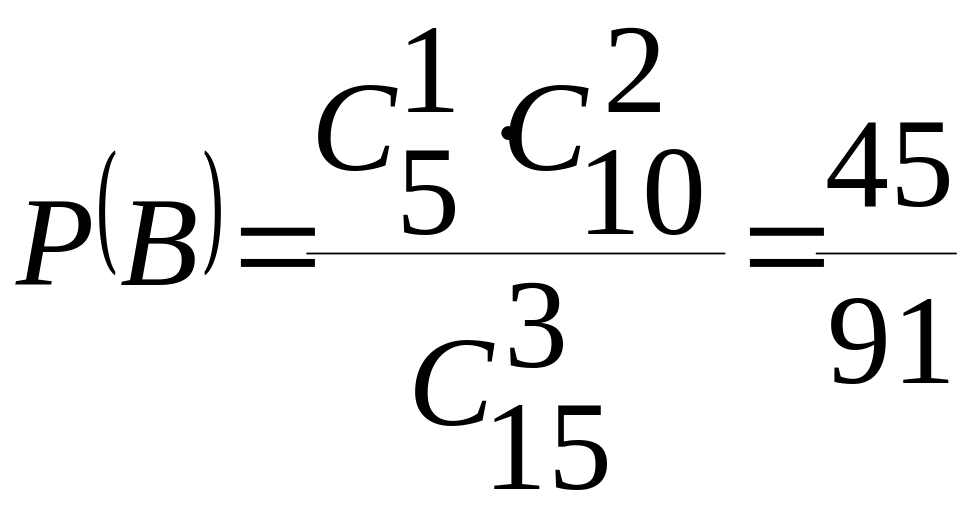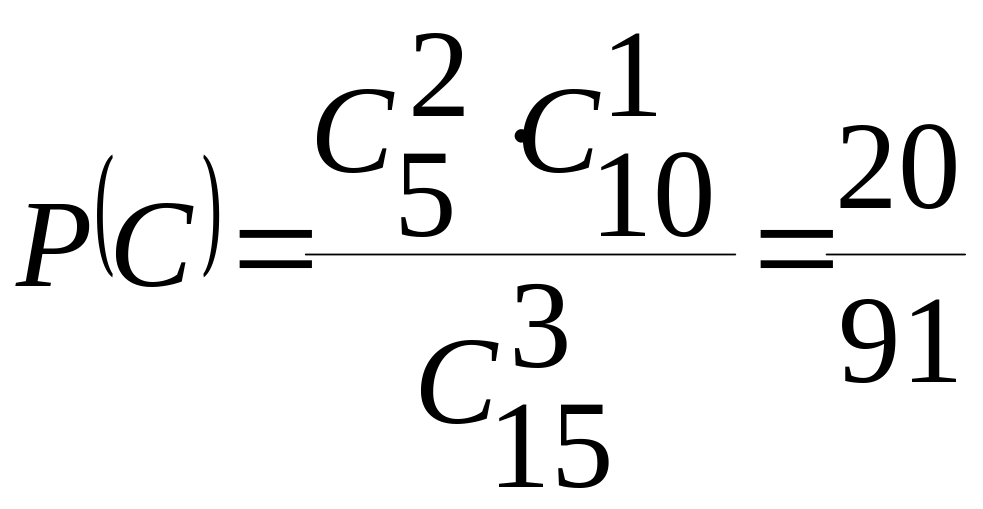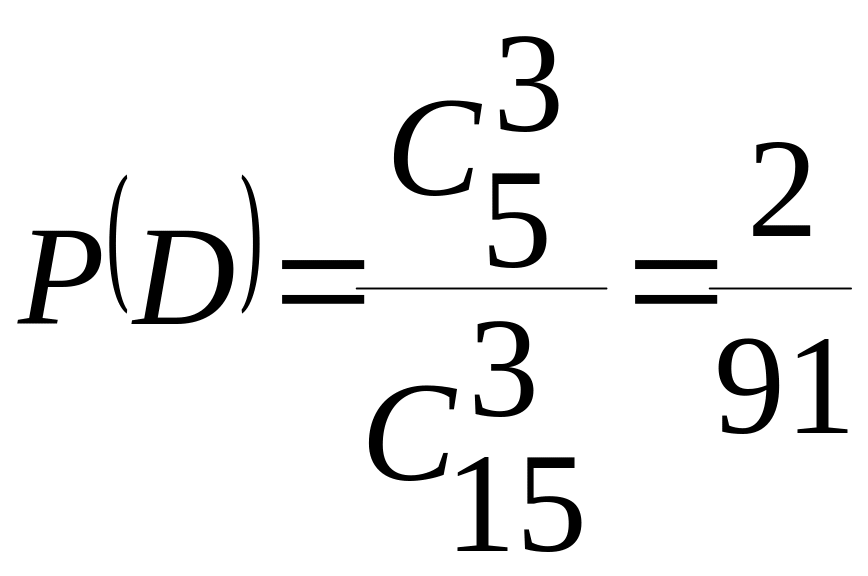тогда

.

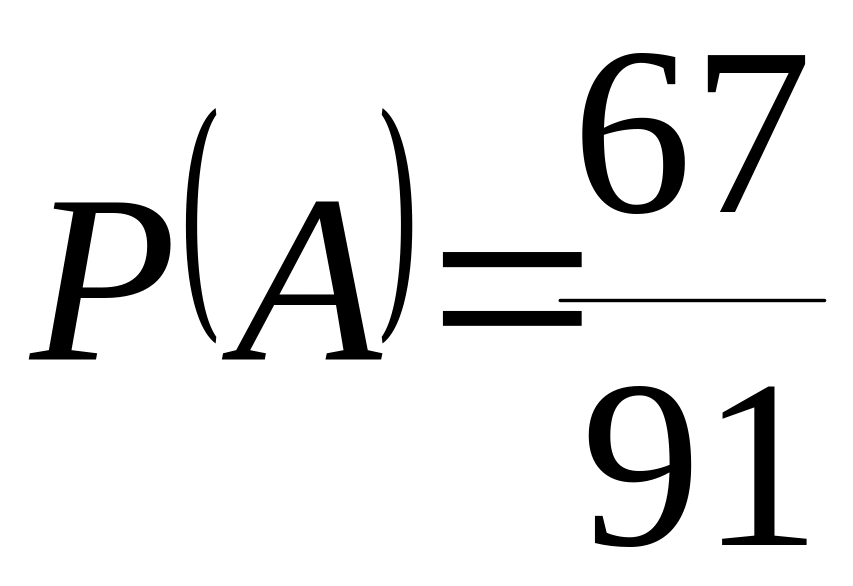§ 1.2.2. Полная группа событий

Теорема. Сумма вероятностей событий , , … , , образующих полную группу, равна единице:

.

Пример 1.24. В ящике 12 белых, 17 черных, 21 синий и 20 красных шаров.

Вынули один шар. Какова вероятность того, что вынутый шар

а) белый; б) черный; в) синий; г) красный; д) белый или черный; е) синий или красный; ж) белый, черный или синий.

Решение.

Имеем .

а) вероятность того, что вынутый шар белый ;

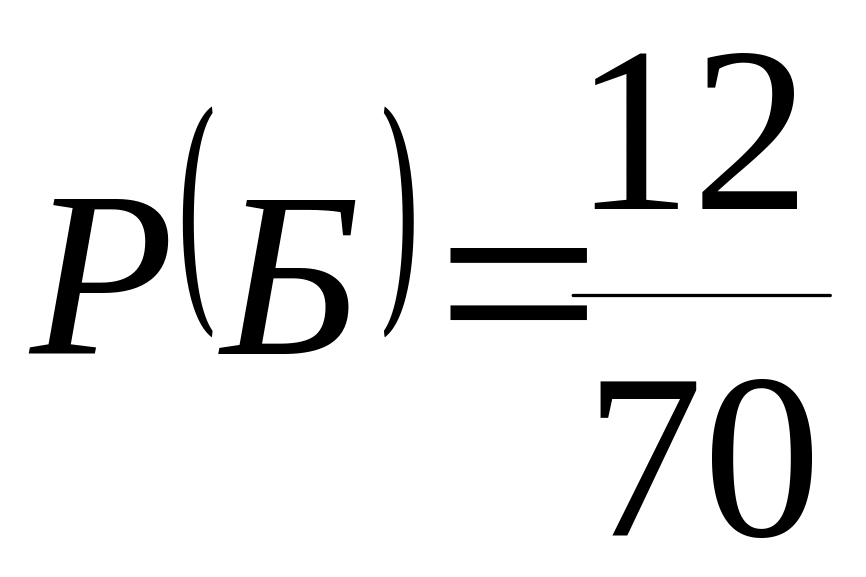б) вероятность того, что вынутый шар чёрный ;

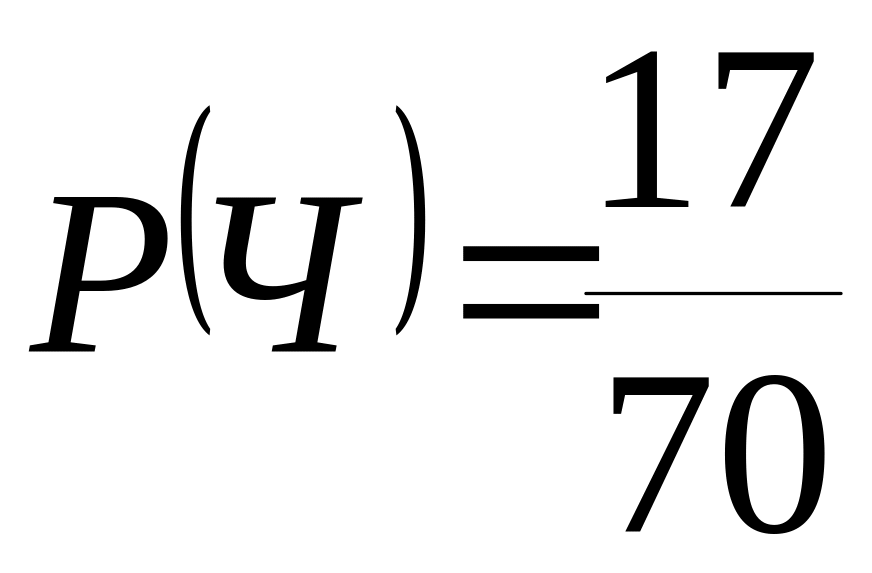в) вероятность того, что вынутый шар синий ;

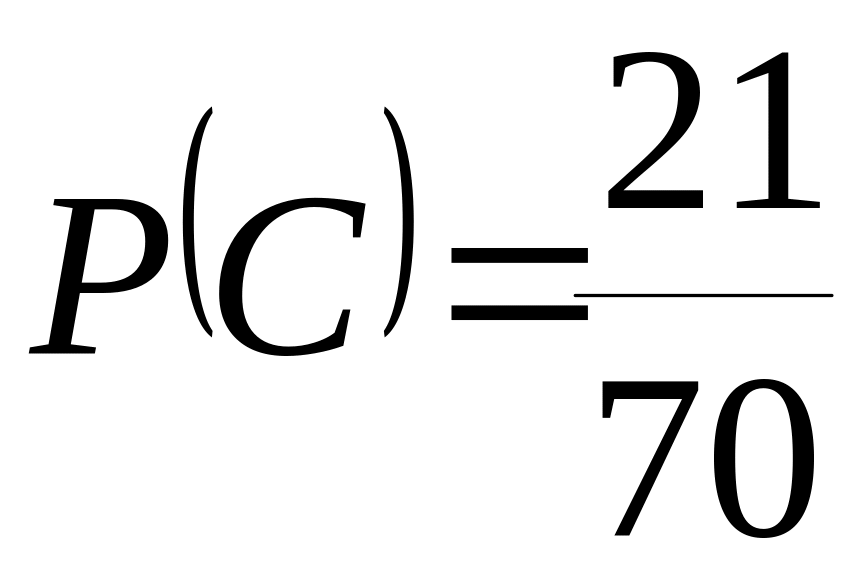г) вероятность того, что вынутый шар красный ;

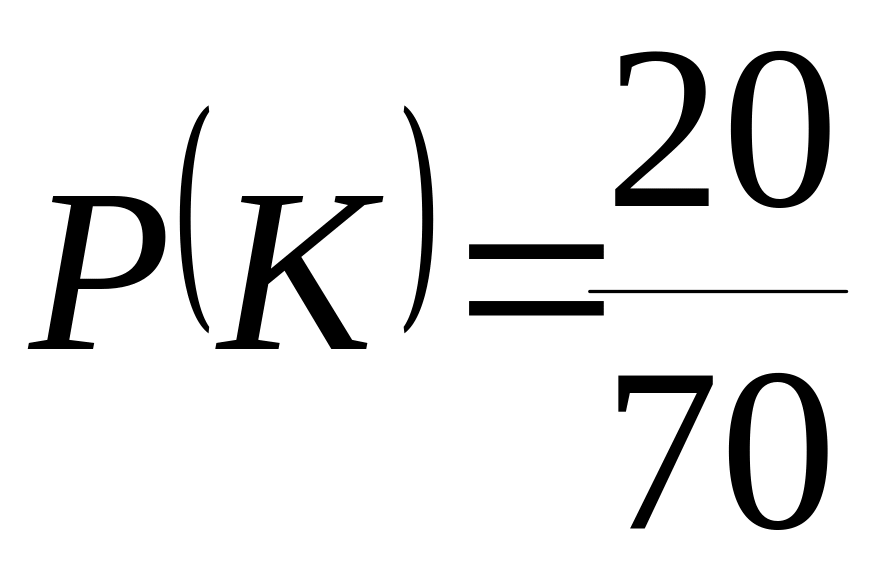д) по теореме сложения вероятностей:

;

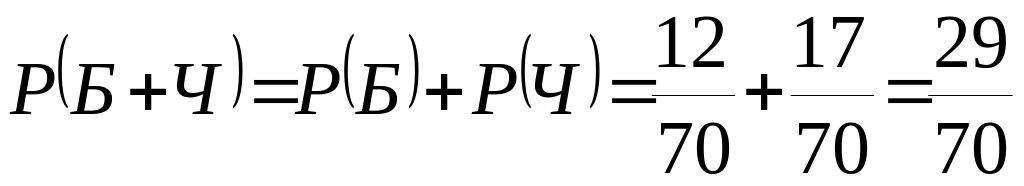е) ;

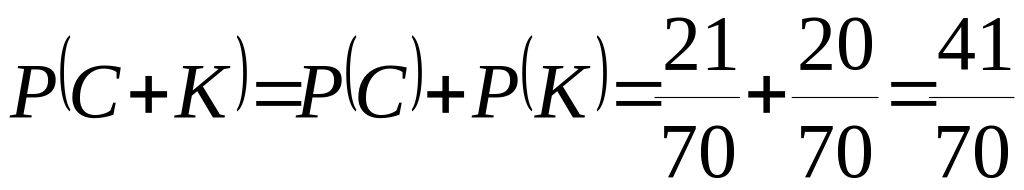ж) события шар белый, черный, синий, красный образуют полную группу событий, поэтому

.
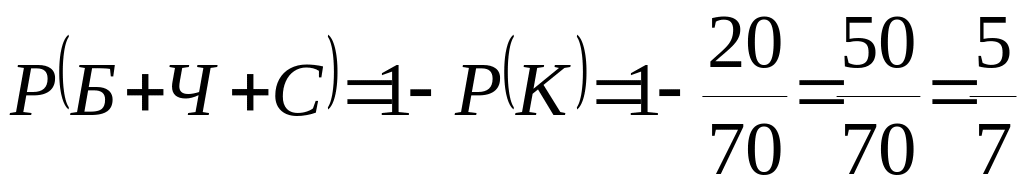