§ 1.1.5. Относительная частота

Относительная частота, наряду с вероятностью, принадлежит к основным понятиям теории вероятностей.

Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.

Таким образом, ,

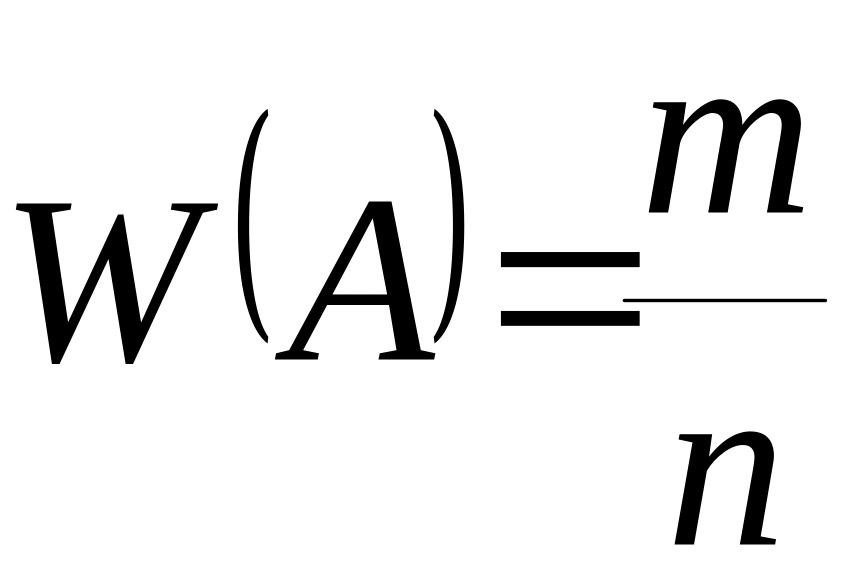где – число появлений события,

– общее число испытаний.

Сопоставляя определения вероятности и относительной частоты, заключаем, что определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически.

Таким образом, вероятность вычисляют до опыта, а относительную частоту – после опыта.

Пример 1.12. Отдел технического контроля обнаружил 4 нестандартных детали в партии из 100 случайно отобранных деталей.

Относительная частота появления нестандартных деталей

.

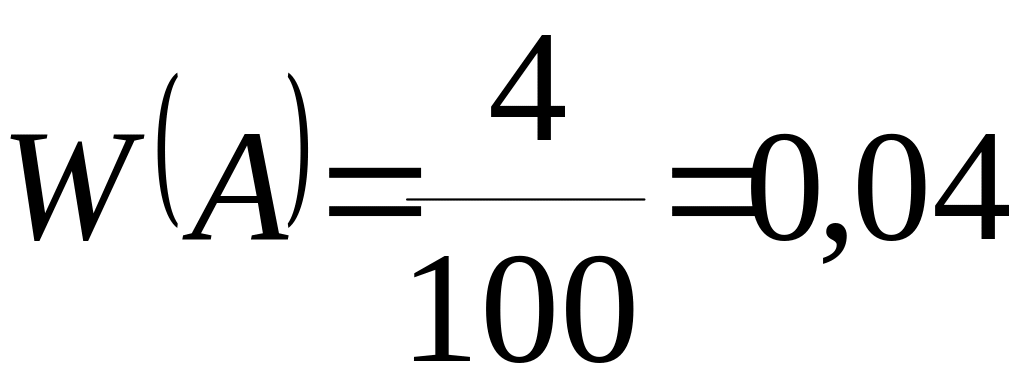Пример 1.13. По цели произведено 50 выстрелов, причем было зарегистрировано 39 попаданий.

Относительная частота поражения цели

.

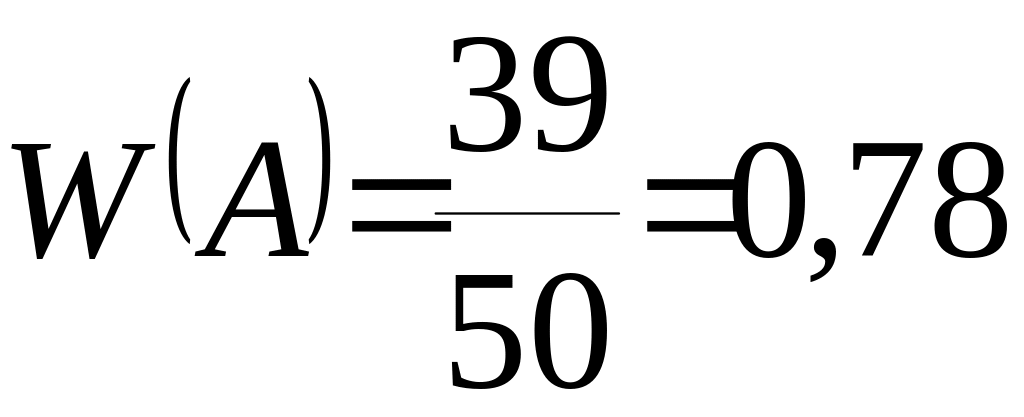Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа.

Оказалось, что это постоянное число есть вероятность появления события.

Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.

Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых бесконечно. В таких случаях классическое определение неприменимо. Также очень часто невозможно представить результат испытания в виде совокупности элементарных событий и основания, позволяющие считать события равновозможными.

Статистическое определение. В качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.

Пример 1.14. В ящике 150 одинаковых деталей, из них 75 окрашены. Наудачу вынимают одну деталь.

Найти вероятность того, что извлечена окрашенная деталь.

Решение. .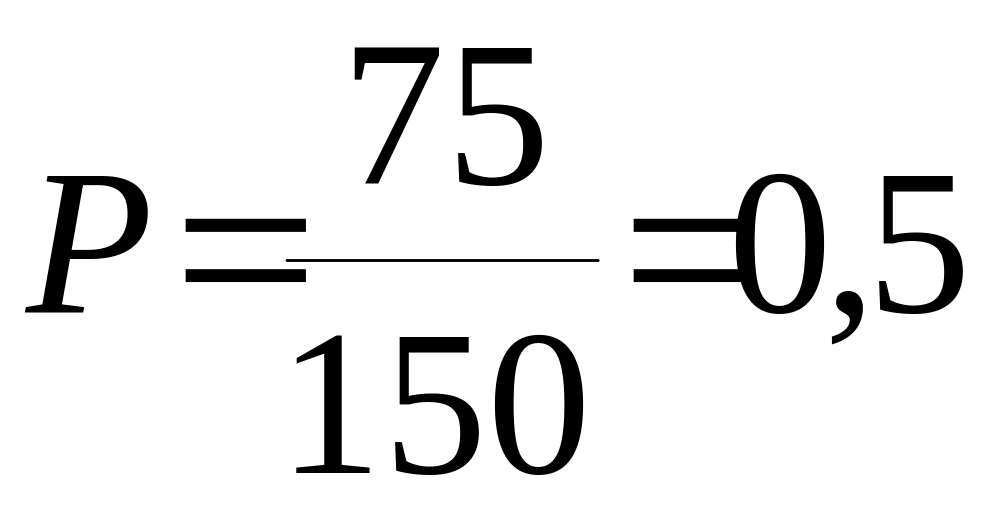

Пример 1.15. Брошена игральная кость.

Найти вероятность того, что выпадет четное число очков.

Решение. Число благоприятных исходов (число очков 2,4,6)

Тогда .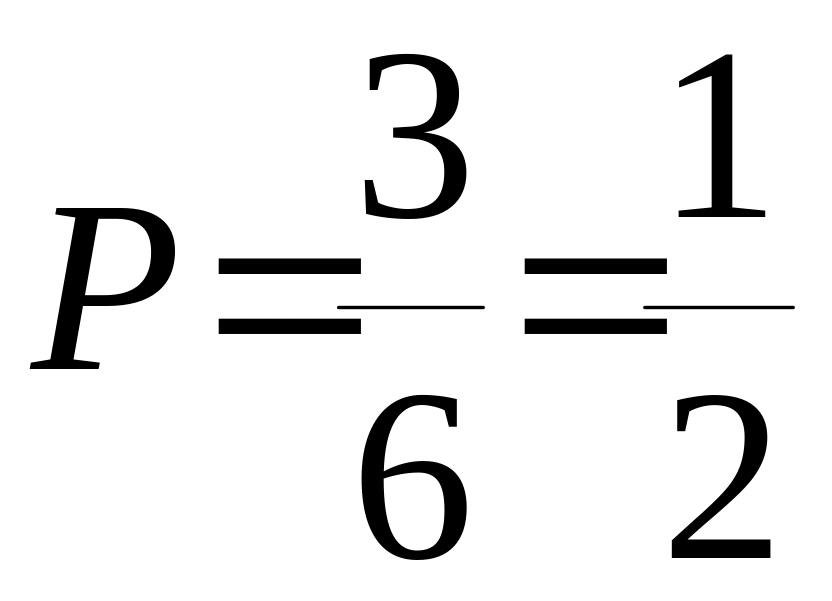

Пример 1.16. В мешочке имеются 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из букв: О, П, Р, С, Т.

Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиках будет слово «спорт».

Решение. .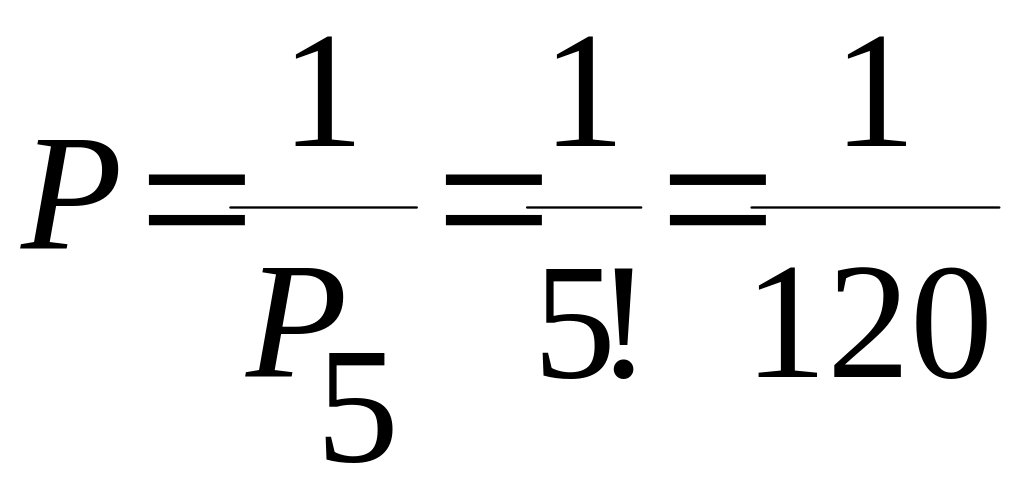

Пример 1.17. На каждой из 6 одинаковых карточек напечатана одна из букв а, т, м, р, с, о. Карточки тщательно перемешаны.

Найти вероятность того, что на 4-х вынутых карточках по одной и расположенных «в одну линию» будет слово «трос».

Решение. .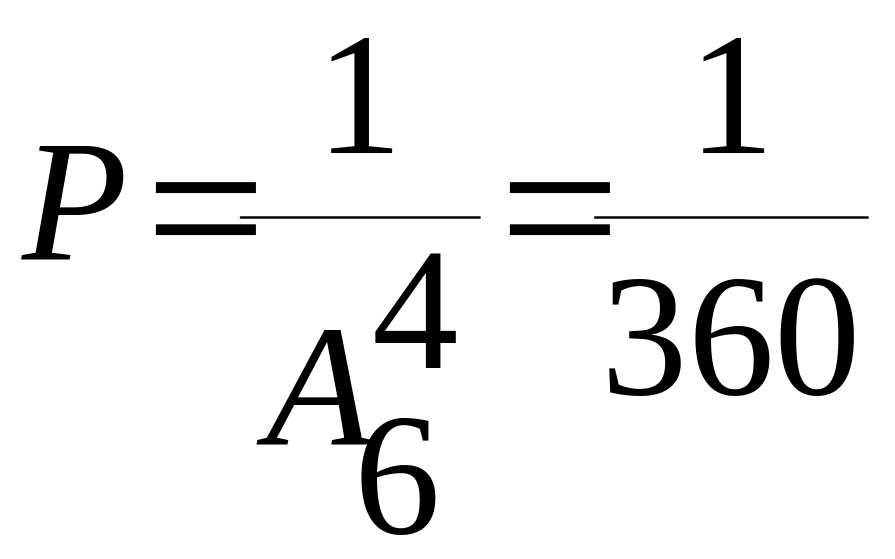

Пример 1.18. В замке на общей оси 5 дисков. Каждый диск разделен на 6 секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка.

Найти того, что при произвольной установке дисков замок можно открыть.

Решение. Замок откроется только при условии, если все диски займут нужное положение. По правилу произведения получим, что:

,

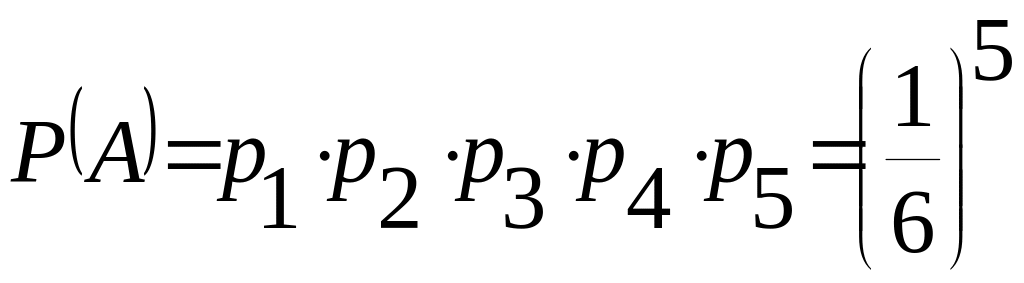где .

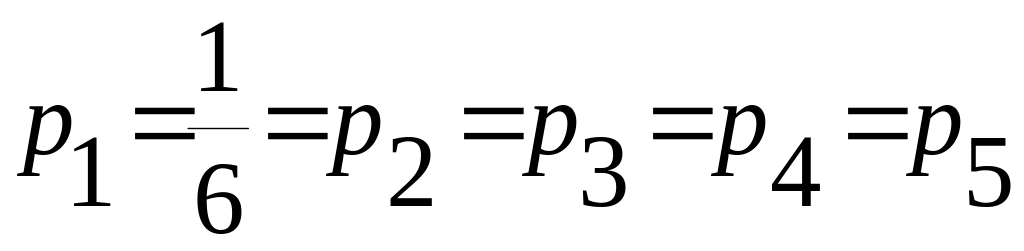Пример 1.19. В книжном ларьке продаются газеты:

15 газет – по 14 рублей,

13 газет – по 11 рублей,

12 газет – по 13 рублей.

Найти вероятность того, что взятые 2 газеты стоят 25 рублей.

Решение. Вероятность того, что взятые две газеты стоят 25 рублей (событие ), равно

,

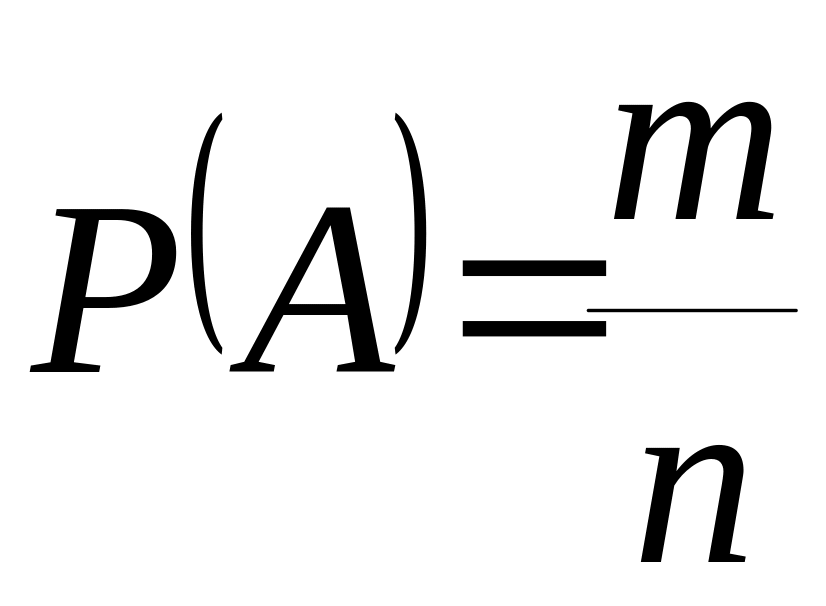где – число всех исходов (сколькими способами можно из 40 газет выбрать две). То есть

,

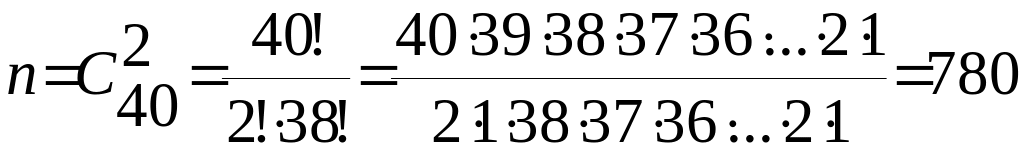– число благоприятных исходов, то есть одна газета за 14 рублей и одна газета по 11 рублей .

, .

Таким образом,

.

Пример 1.20. При стрельбе из винтовки относительная частота попадания в цель оказалась равной .

Найти число попаданий, если всего было произведено 120 выстрелов.

Решение. ,

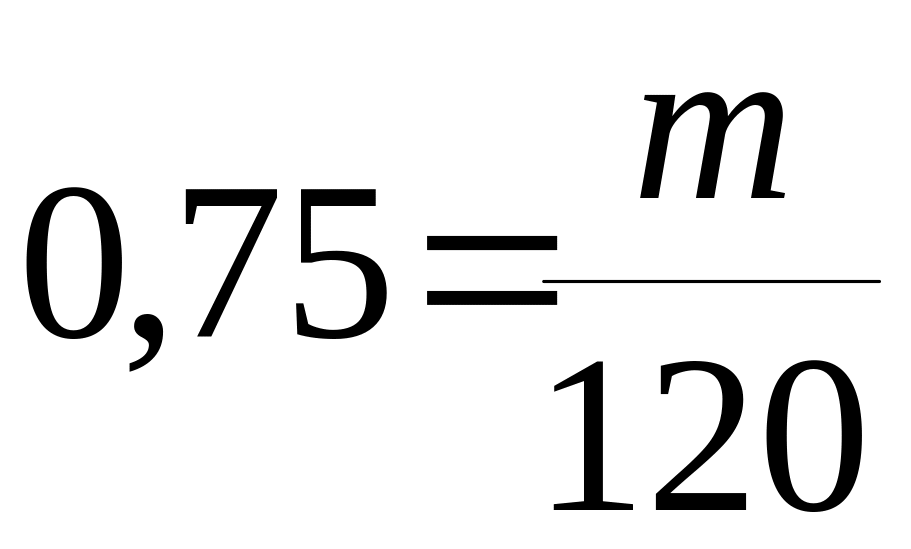тогда .