§ 2.6.11. Коррелированность и зависимость случайных величин
Две случайные величины и называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля; и называют некоррелированными величинами, если их корреляционный момент равен нулю.
Две коррелированные величины также и зависимы.
§ 2.6.12. Линейная регрессия
Рассмотрим двумерную случайную величину , где и – зависимые случайные величины. Представим одну из величин, как функцию другой. Ограничимся приближенным представлением величины в виде линейной функции величины [3]:
,
где
и
– параметры, подлежащие определению.
Это можно сделать различными способами:
наиболее распространенный из них –
метод наименьших квадратов.
Функцию
называют «наилучшим приближением»
,
в смысле метода наименьших квадратов,
если математическое ожидание
принимает наименьшее возможное значение;
функцию
называют среднеквадратической
регрессией
на
.
Теорема. Линейная средняя квадратическая регрессия на имеет вид
,
где
;
– коэффициент
корреляции величин
и
.
Коэффициент
называют коэффициентом
регрессии
на
,
а прямую:
,
(52)
называют прямой среднеквадратической регрессии на .
Минимальное
значение функции
равно
.
Величину
называют остаточной
дисперсией случайной
величины
относительно случайной величины
;
она характеризует величину ошибки,
которую допускают при замене
линейной функцией
.
При
остаточная дисперсия равна нулю; другими
словами, при этих крайних значениях
коэффициента корреляции не возникает
ошибки при представлении
,
в виде линейной функции от
.
Итак, если коэффициент корреляции , то и связаны линейной функциональной зависимостью.
Аналогично можно получить прямую среднеквадратической регрессии на :
(53)
(
–
коэффициент регрессии
на
)
и остаточную дисперсию
величины
относительно
.
Если , то обе прямые регрессии, как видно из (52) и (53), совпадают.
Из уравнений (52)
и (53) следует, что обе прямые регрессии
проходят через точку
,
которую называют центром
совместного распределения величин
и
.
Пример 2.42. Система случайных величин подчинена закону распределения с плотностью:
, в
области
и , вне этой области.
Область
определяется неравенствами 
,
.
Найти
,
,
определить коэффициент корреляции
.
Решение. Вычислим математическое ожидание случайной величины :
.
Точно так же
.
Вычислим среднее квадратическое отклонение:
*
Найдем интеграл:
**
**
.
Тогда
*
.
Следовательно: 
.
Определим ковариацию:
**
Используя формулу интегрирования по частям, получим
**
***
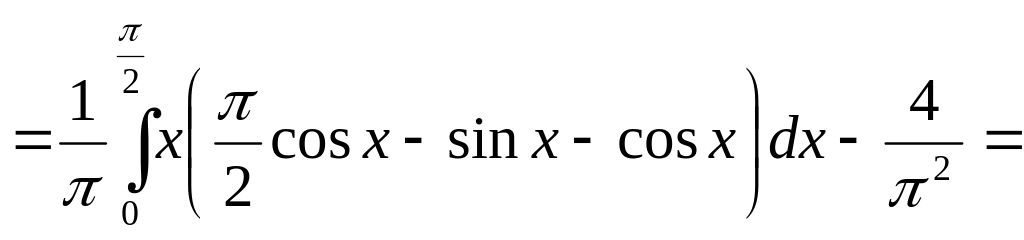используя формулу интегрирования по частям, получим
***
.
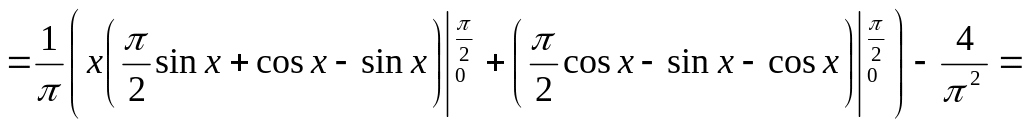
Тогда
Глава 3. Примеры для самостоятельной работы
В книжном киоске продаются газеты:
10 + (* )- газет стоимостью по 15 рублей,
12 +(*) - газет стоимостью по 12 рублей,
15 +(*) - газет стоимостью по 10 рублей.
Найти вероятность того, что взятые две газеты стоят 22 рубля.
В ящике 2 · (*) белых, 3 · (*) черных и 4 · (*) синих шара.
Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно.
Найти вероятность того, что при первом испытании появится синий шар, при втором – белый, при третьем – синий шар, при четвертом – черный шар.
В урне 9 · (*) шаров, из них 4 · (*) – белых, остальные черные. Вынули подряд 3 · (*) шаров, причем каждый вынутый шар возвращается в урну перед извлечением следующего, а затем шары в урне перемешиваются.
Найти вероятность того, что из 3 ·(*) вынутых шаров, будет 2 ·(*)- белых.
Производятся четыре независимых выстрела по цели. Вероятности попадания при различных выстрелах различны и равны:
,
,
,
.
Найти вероятности
(
)
ни одного, одного, двух, трех и четырех
попаданий; вероятности (
)
хотя бы одного попадания; вероятности
(
)
не менее двух попаданий.
В первом и во втором ящиках (*)+7 шаров:
1-й ящик 2-й ящик
(*)+1 шара с номером 1 3 шара с номером 1
2 шара с номером 2 3 шара с номером 2
3 шара с номером 3 1 шар с номером 3
1 шар с номером 4 (*) шаров с номером 4
Пусть X – номер шара, вынутого из первого ящика, Y – номер шара, вынутого из второго ящика.
Из каждого ящика вынули по шару.
Найти математическое ожидание случайных величин X и Y; дисперсию и коэффициент корреляции.
Где (*) – последняя цифра шифра.