Свойства вероятности

Свойство 1. Вероятность достоверного события равна единице:

.

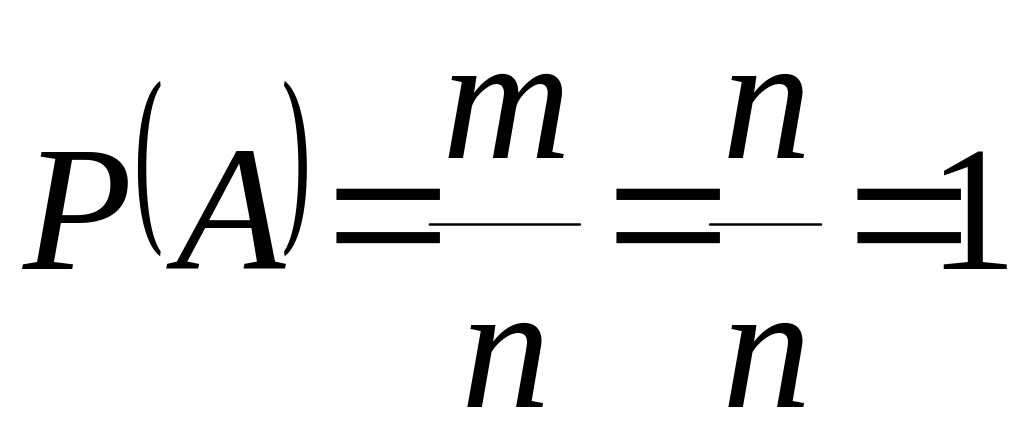Свойство 2. Вероятность невозможного события равна нулю.

.

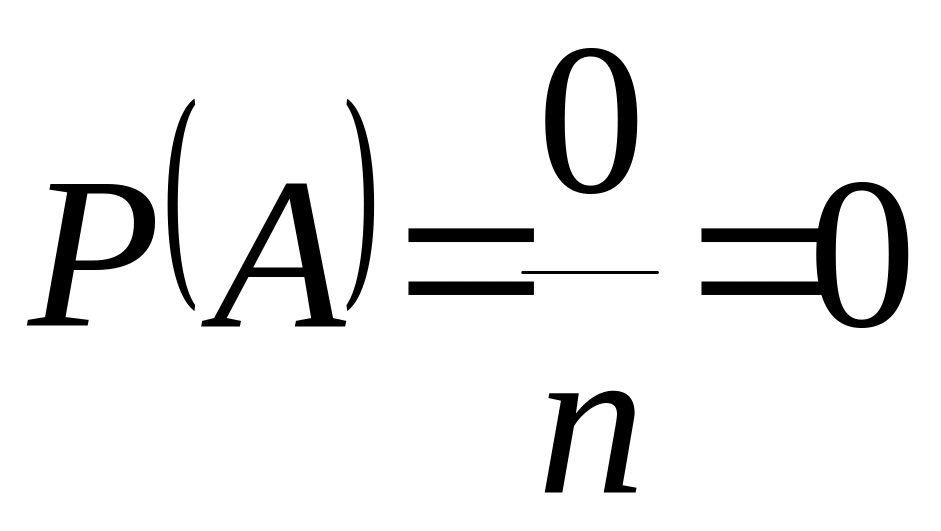Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

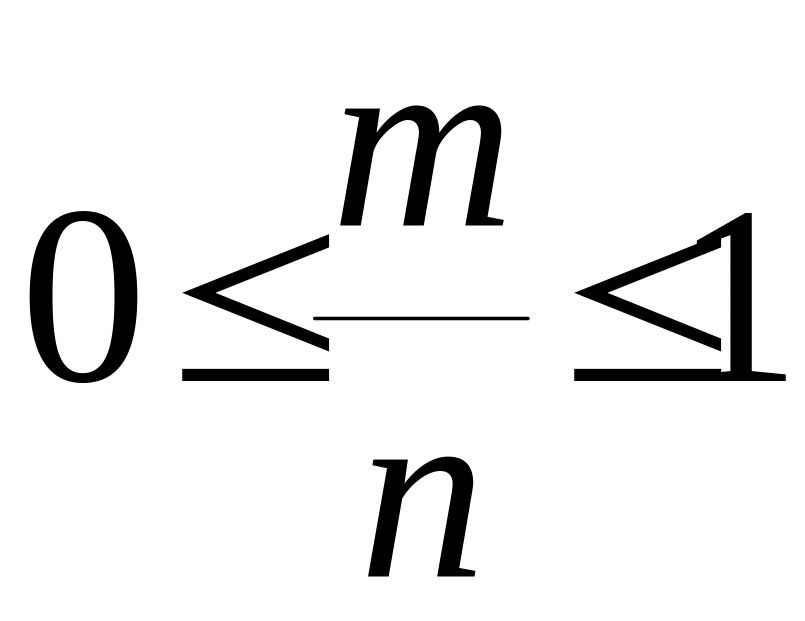Так как , то . Тогда .

§ 1.1.3. Основные формулы комбинаторики

При непосредственном вычислении вероятностей часто используют формулы комбинаторики.

Перестановками называют комбинации, состоящие из одних и тех же « » различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

,

где , .

Пример 1.6. Сколько четырёхзначных чисел можно составить из цифр 1, 2, 3, 4, если каждая цифра входит в изображение числа только один раз.

.

Размещениями называют комбинации, составленные из « » различных элементов по « » элементов, которые отличаются либо составом элементов, либо их порядком.

.

Пример 1.7. Сколько можно составить сигналов из 7 флажков различного цвета, взятых по 2?

Искомое число сигналов .

Сочетаниями называют комбинации, составленные из « » различных элементов по « » элементов, которые отличаются хотя бы одним элементом.

.

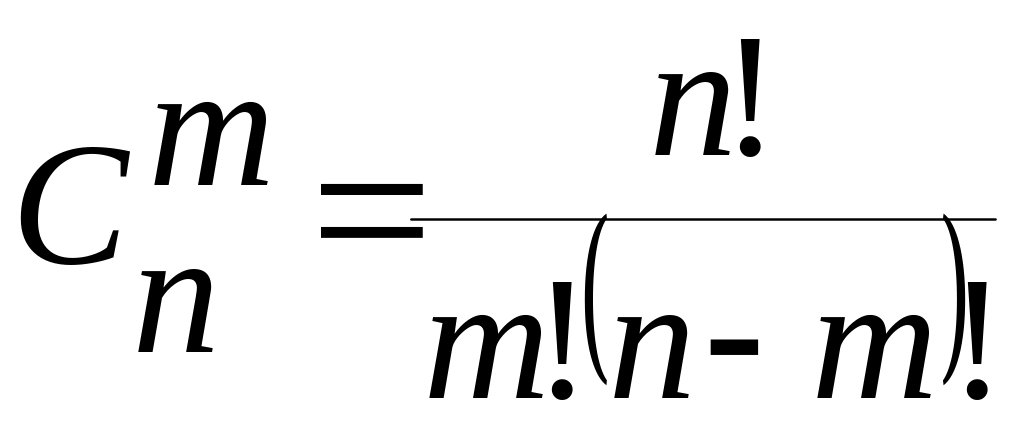Пример 1.8. Сколько есть способов для выбора двух деталей из ящика, содержащего 20 деталей?

.

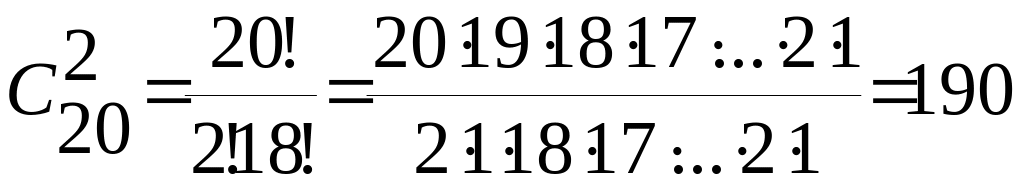При решении задач комбинаторики используют следующие правила:

1. Правило суммы. [3,4].

Если некоторый объект А может быть выбран из совокупности объектов « » способами, а другой объект В может быть выбран « » способами, то выбрать либо А, либо В можно способами.

2. Правило произведения.

Если объект А можно выбрать из совокупности объектов « » способами и после каждого такого выбора объект В можно выбрать « » способами, то пара объектов А и В (А,В), в указанном порядке, может быть выбрана способами.

§ 1.1.4. Примеры непосредственного вычисления вероятностей

Пример 1.9. Набирая номер телефона, абонент

а) забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.

Решение. Известно, что – количество всех возможных цифр, равно 10 (0,1,2,3,4,5,6,7,8,9), а – количество благоприятных исходов, равно 1, так как только одна цифра подходит. Тогда

.

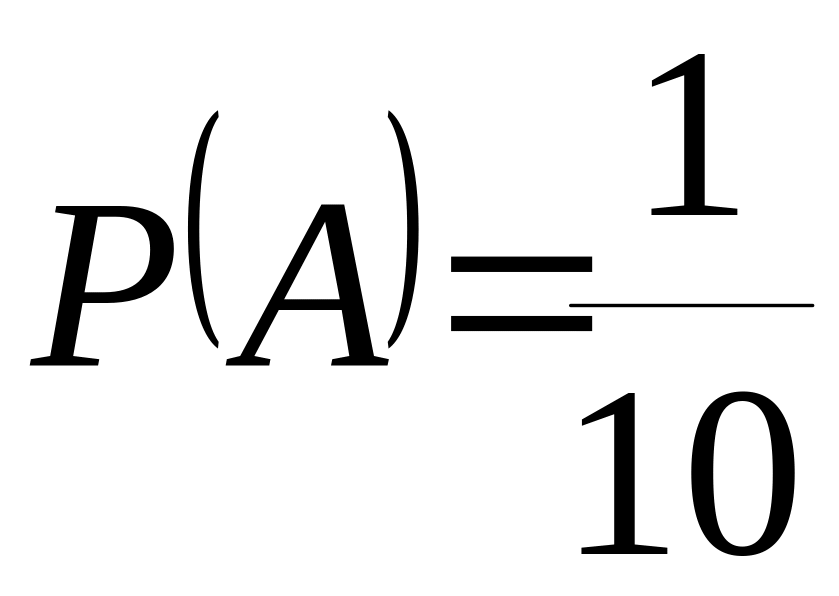б) забыл две цифры, помня только то, что эти цифры различны. Найти вероятность того, что набраны нужные цифры.

Решение. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из 10 по 2. Количество всех возможных исходов равно

.

Таким образом, .

Заметим, что эти исходы несовместны, а также, что подходит только одна комбинация цифр, поэтому . Следовательно,

.

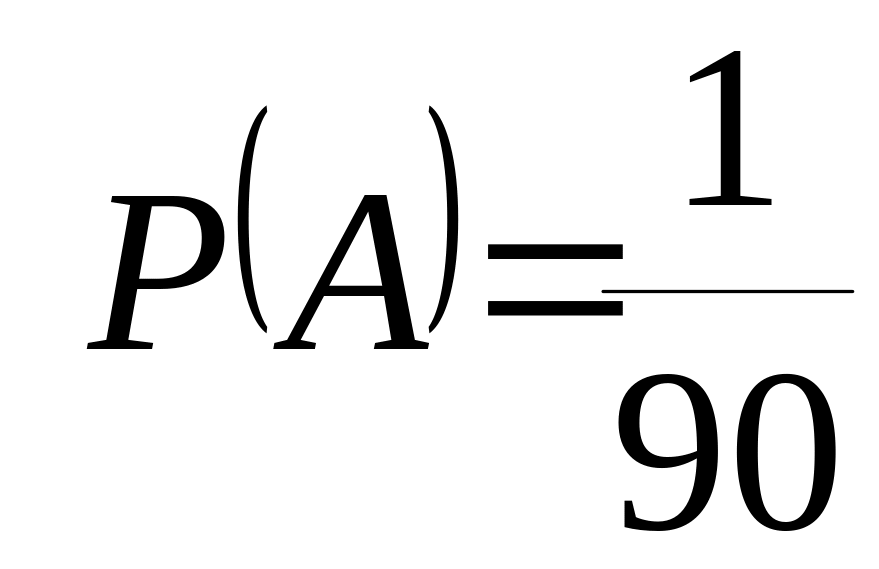Пример 1.10. Брошены две игральные кости.

Найти вероятность того, что сумма выпавших очков равна 4.

Решение. Общее число равновозможных исходов равно ( ).

Среди них, благоприятствующих событию , равно - это комбинации: .

Следовательно, .

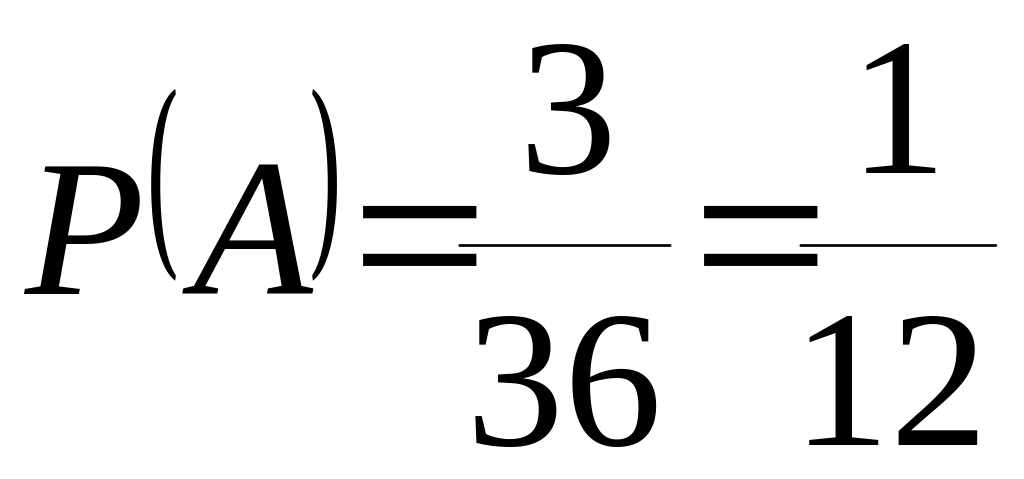Пример 1.11. В лотерее 5000 билетов. Два билета с выигрышем по 10 000 рублей, десять билетов с выигрышем по 1000 рублей. Пятьдесят билетов с выигрышем по 500 рублей, 100 билетов с выигрышем по 50 рублей, 500 билетов с выигрышем по 5 рублей. Остальные билеты невыигрышные.

Какова вероятность того, что при покупке одного билета выигрыш будет не меньше 50 рублей.

Решение. Число благоприятствующих событий

.

Количество всех исходов (количество билетов) .

Тогда вероятность того, что выигрыш по одному билету будет не меньше 50 рублей, равна

.
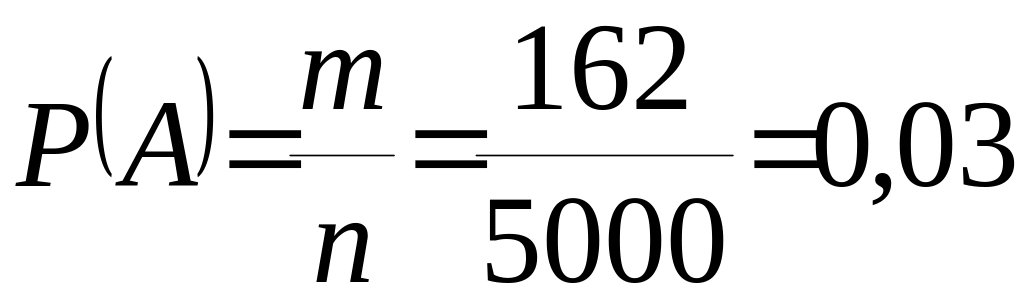