§ 2.6.10. Числовые характеристики системы двух случайных величин

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции [3].

Корреляционным моментом случайных величин и называют математическое ожидание произведения отклонений этих величин:

.

Для вычисления корреляционного момента дискретных величин используют формулу:

,

а для непрерывных величин формулу

.

Корреляционный момент служит для характеристики связи между величинами и . Как будет показано ниже, корреляционный момент равен нулю, если и независимы; следовательно, если корреляционный момент не равен нулю, то и – зависимые случайные величины.

Замечание 1. Учитывая, что отклонения есть центрированные случайные величины, корреляционный момент можно определить как математическое ожидание произведения центрированных случайных величин:

.

Замечание 2. Легко убедиться, что корреляционный момент можно записать в виде .

Теорема 1. Корреляционный момент двух независимых случайных величин и равен нулю.

Коэффициентом корреляции случайных величин и называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин: . (51)

Так как размерность равна произведению размерностей величин и , имеет размерность величины , имеет размерность величины , то – безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.

Очевидно, коэффициент корреляции независимых случайных величин равен нулю (так как ).

Теорема 2. Абсолютная величина корреляционного момента двух случайных величин и не превышает среднего геометрического их дисперсий:

.

Теорема 3. Абсолютная величина коэффициента корреляции не превышает единицы:

.

Пример 2.41. В первом ящике 6 шаров, во втором ящике также 6 шаров:

1-й ящик	2-й ящик
1 шар с № 1	2 шара с № 1
2 шара с № 2	3 шара с № 2
3 шара с № 3	1 шар с № 3

Пусть – номер шара, вынутого из первого ящика, – номер шара, вынутого из второго ящика. Из каждого ящика вынули по шару. Найти дисперсию случайных величин и , коэффициент корреляции .

Решение. Запишем закон распределения системы случайных величин .

Случайная величина может принимать следующие значения: .

Случайная величина может принимать следующие значения: .

Вероятность того, что из первого ящика будет вынут шар с № 1 и из второго – шар с № 1, равна

.

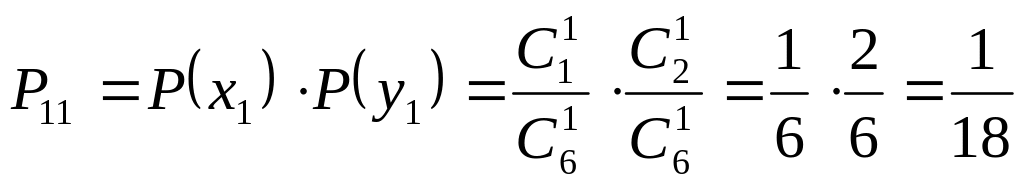Вероятность того, что из первого ящика будет вынут шар с номером 2, а из второго – шар с номером 1 равна:

.

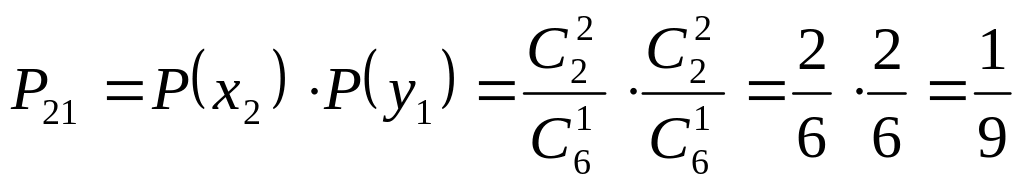Аналогичным образом вычисляем все остальные вероятности. В результате закон распределения будет иметь следующий вид (см. табл.36).

Таблица 36

	1	2	3
1
2
3

Для нахождения математического ожидания случайных величин и выпишем ряды распределения для величин и (так как они независимы).

Заметим, что

, ,

	1	2	3

Аналогично для

	1	2	3

Тогда ,

.

Для того чтобы найти дисперсию случайных величин и , запишем закон распределения для и (табл. 37).

Таблица 37

Тогда дисперсия случайной величины

.

.

Отсюда

, .

А коэффициент корреляции равен

.

.

Тогда .