§ 2.5.4. Распределение Стьюдента

Пусть – нормальная случайная величина, причем , , а – независимая от величина, которая распределена по закону с степенями свободы. Тогда величина

(21)

имеет распределение, которое называют -распределением или распределением Стьюдента с степенями свободы.

Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределенной по закону «хи-квадрат» с степенями свободы, деленной на , распределено по закону Стьюдента с степенями свободы.

С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

В приложении 4 представлены критические точки распределения Стьюдента.

§ 2.5.5. Распределение f Фишера-Снедекора

Если и – независимые случайные величины, распределенные по закону со степенями свободы и , то величина

(22)

имеет распределение, которое называют распределением F Фишера-Снедекора со степенями свободы и (иногда его обозначают через ).

Плотность этого распределения

,

где

.

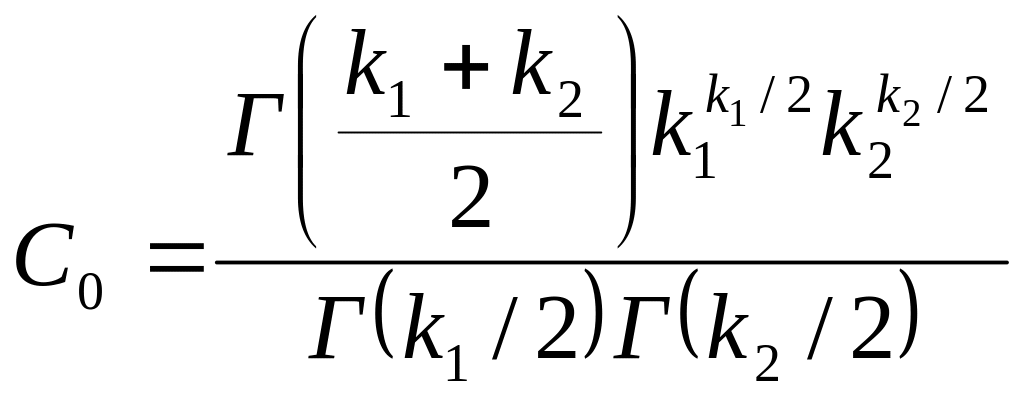Распределение F определяется двумя параметрами – числами степеней свободы.

На рис. 9 представлен график плотности вероятности распределения Фишера-Снедекора.

Рис. 9. Плотность вероятности распределения Фишера-Снедекора

Заметим, что случайная величина с F-распределением имеет следующие числовые характеристики (см. табл. 28) [1].

Таблица 28

Математическое ожидание	,
Мода	,
Дисперсия	,
Асимметрия	,
Эксцесс	,
Начальные моменты	, , , ,
Центральные моменты	, ,

В приложении 5 представлены критические точки распределения Фишера-Снедекора.

Свойства распределения Фишера-Снедекора [1]

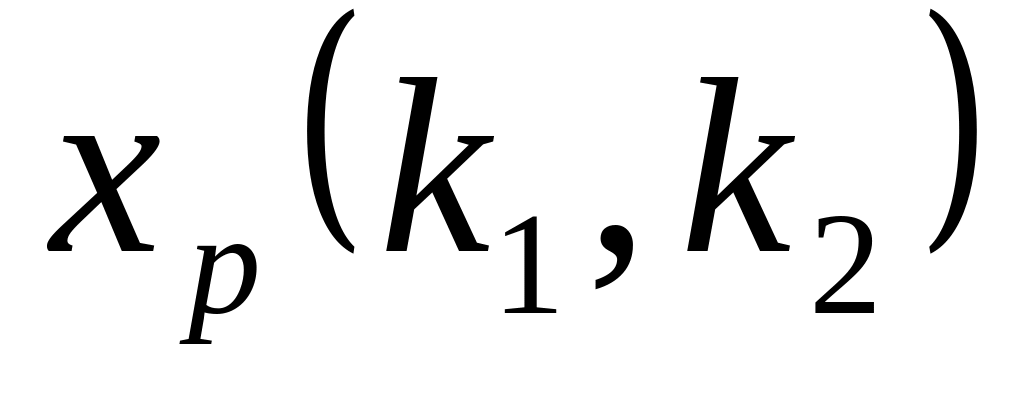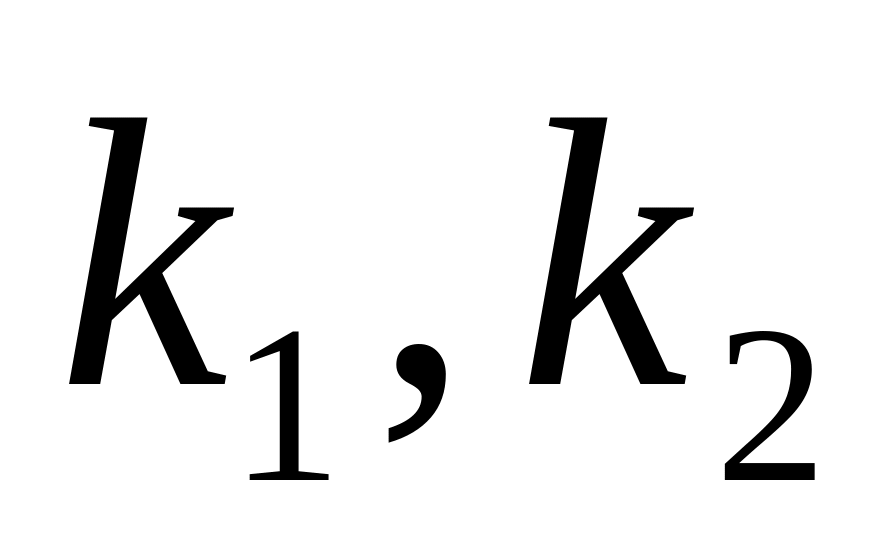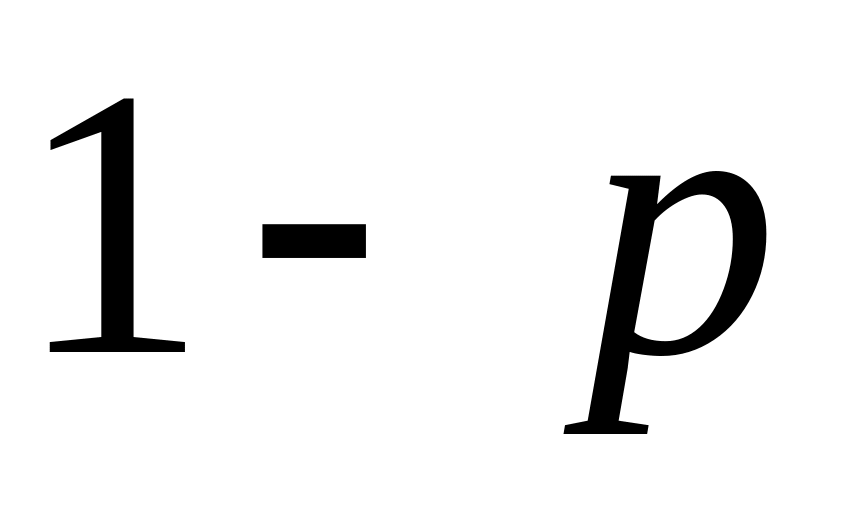1. Квантиль порядка F-распределения с степенями свободы и квантиль порядка F-распределения с 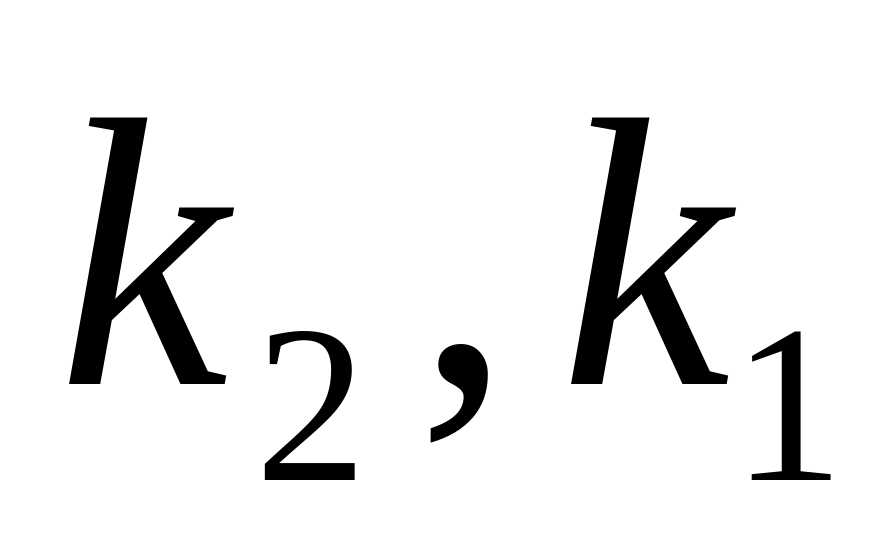степенями свободы связаны соотношением 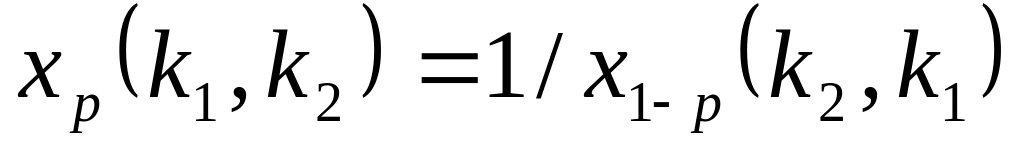. Этому соотношению эквивалентно соотношение

.

Приведенные соотношения делают ненужным табулирование F-распределения для значений аргумента . При необходимости найти значение функции распределения для следует перейти к значению аргумента, равному , и воспользоваться последним из приведенных выше соотношений.

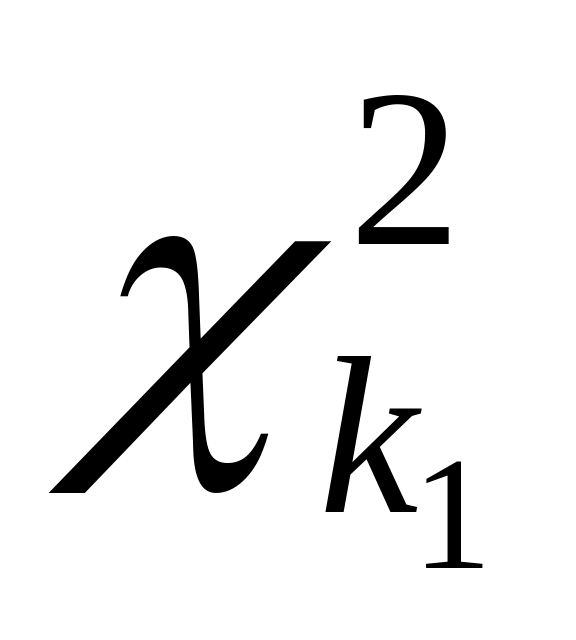2. Если и 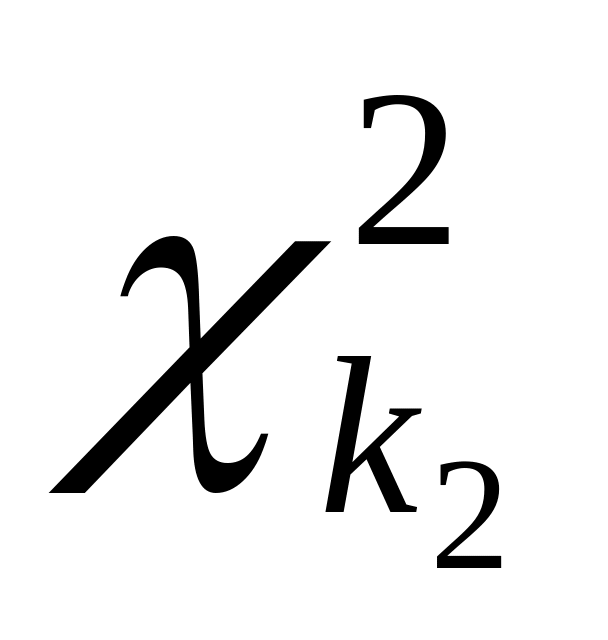– независимые случайные величины, имеющие -распределение с и степенями свободы соответственно, то случайная величина

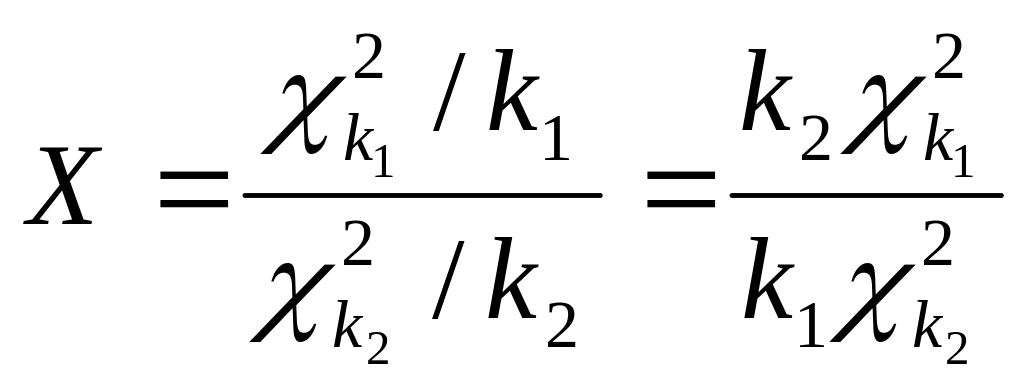
имеет F-распределение с , степенями свободы.

3. Если случайная величина 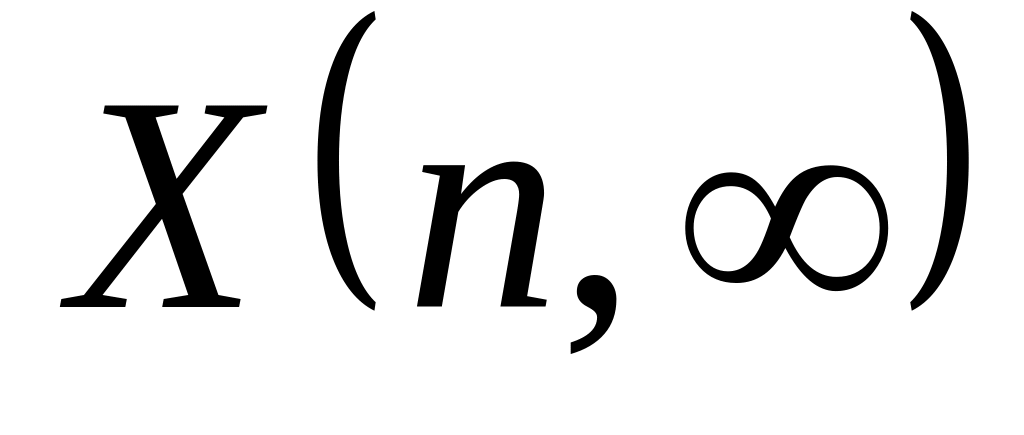имеет F-распределение с параметрами 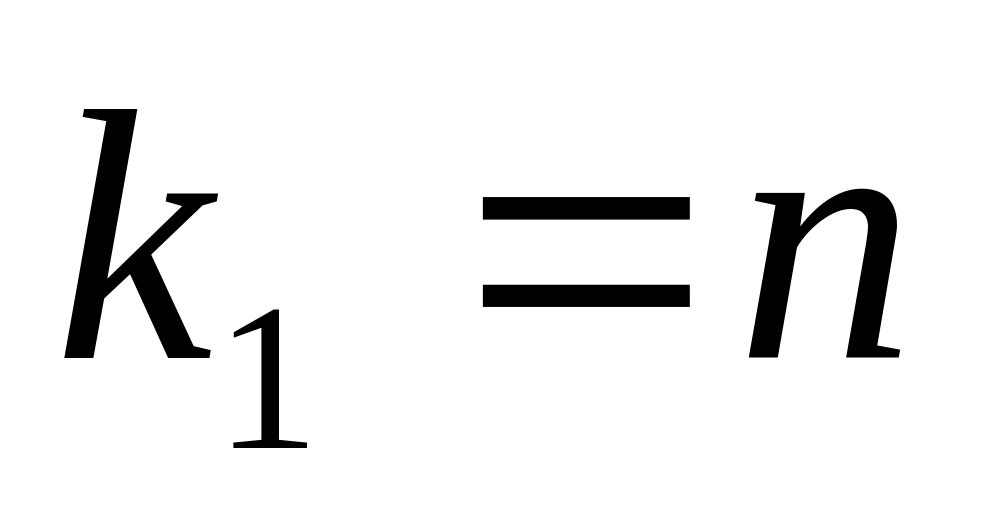, , 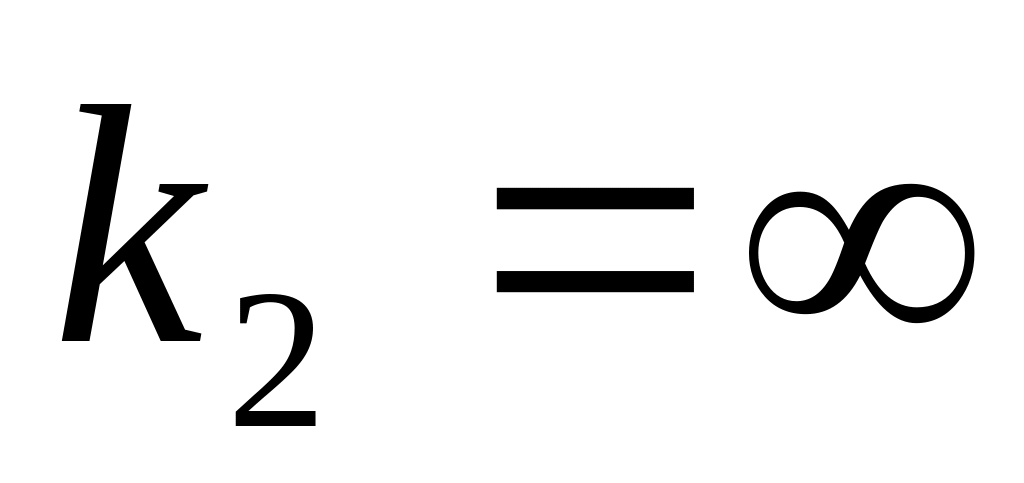а случайная величина 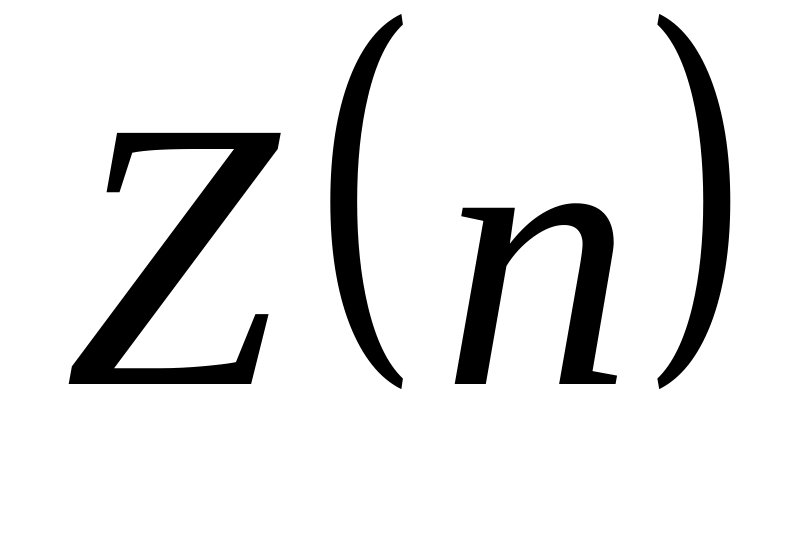имеет -распределение с степенями свободы, то справедливы следующие соотношения:

, ,

~ .

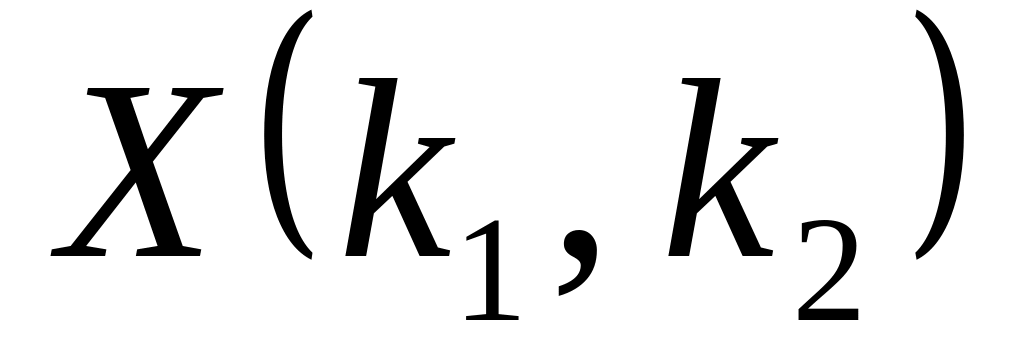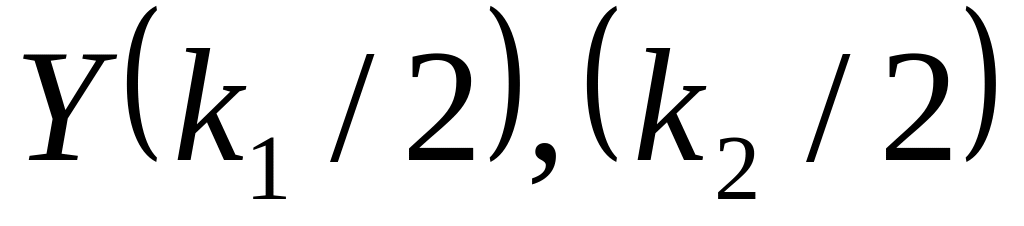4. Случайная величина , имеющая F-распределение с и степенями свободы, связана со случайной величиной , имеющая бета-распределение первого рода с параметрами 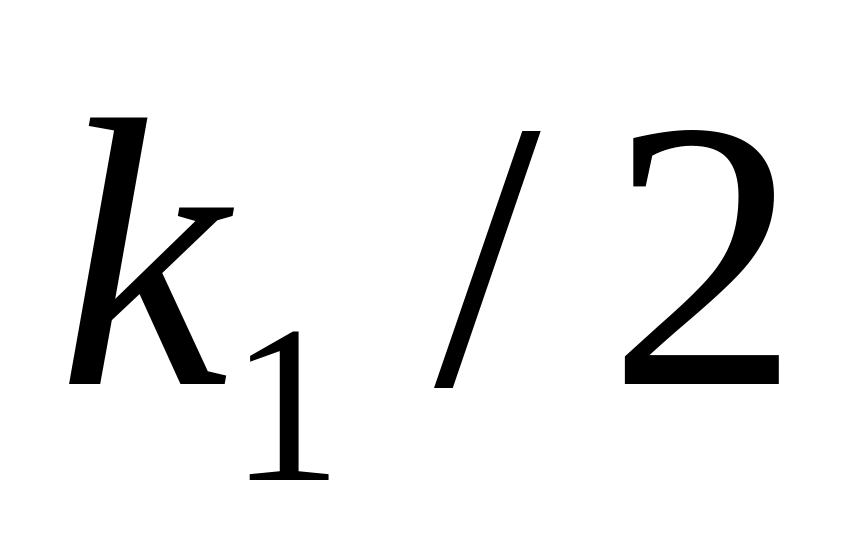, , 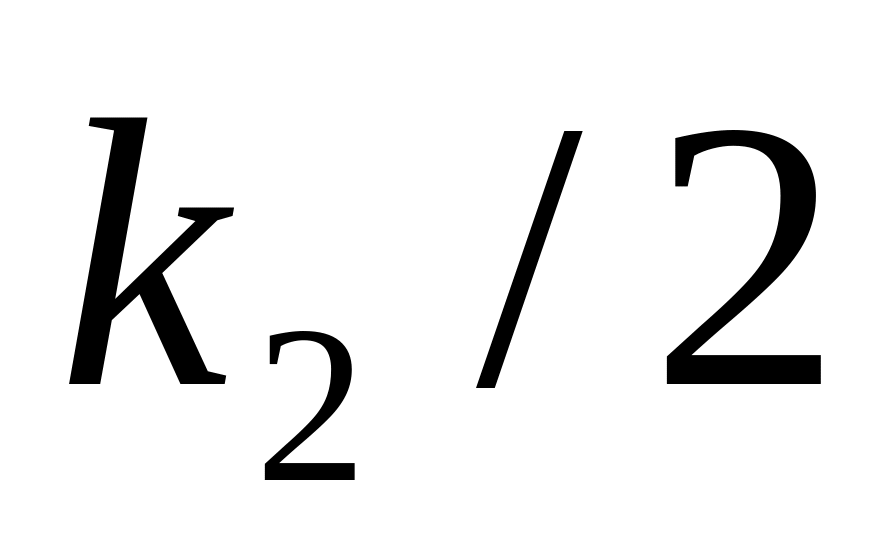соотношениями

.

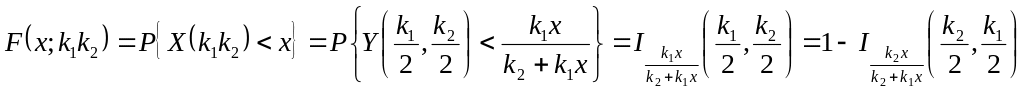
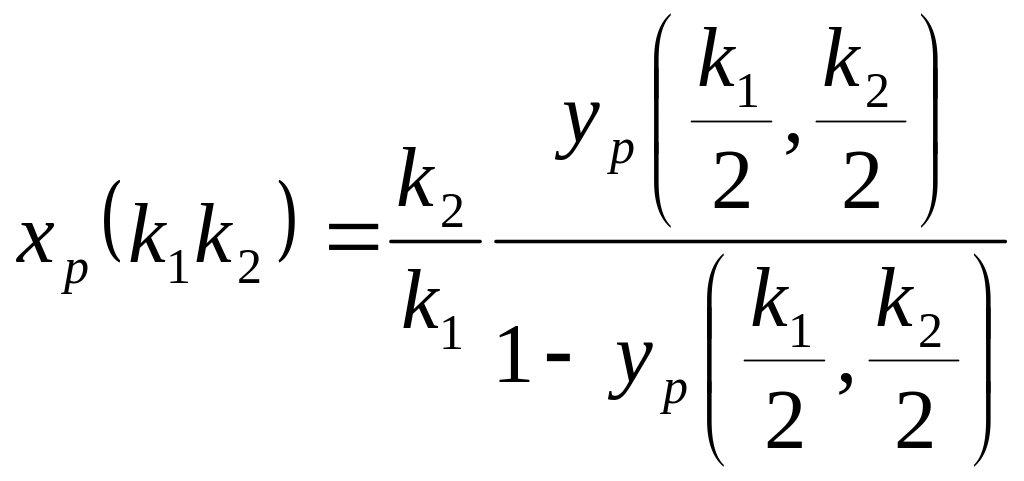Первое из этих соотношений используется для вычисления значений функции распределения Фишера-Снедекора с помощью таблиц неполной бета-функции.

Если – четное число, то F-распределение с параметрами связано с биноминальным распределением с числом испытаний и вероятностью успеха соотношением

,

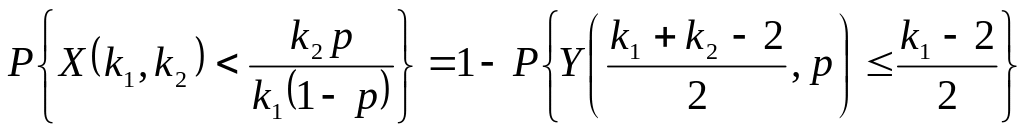где – случайная величина, распределенная по биноминальному закону с параметрами .

5. F-распределение сводится к бета-распределению второго рода (распределение VI – по классификации Пирсона).

6. При возрастании и F-распределение приближается к нормальному распределению.

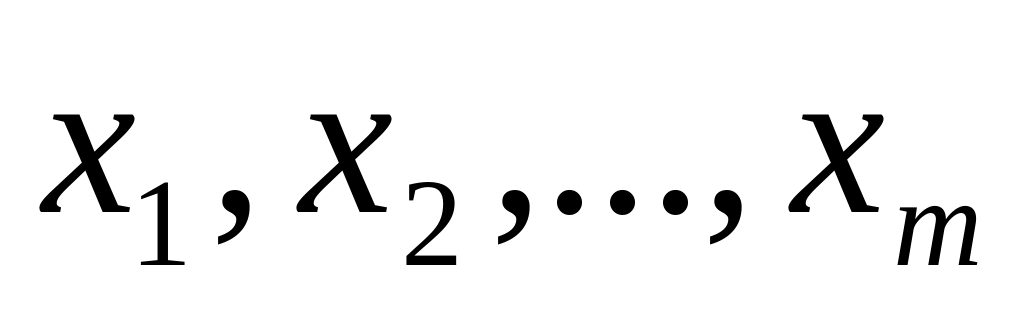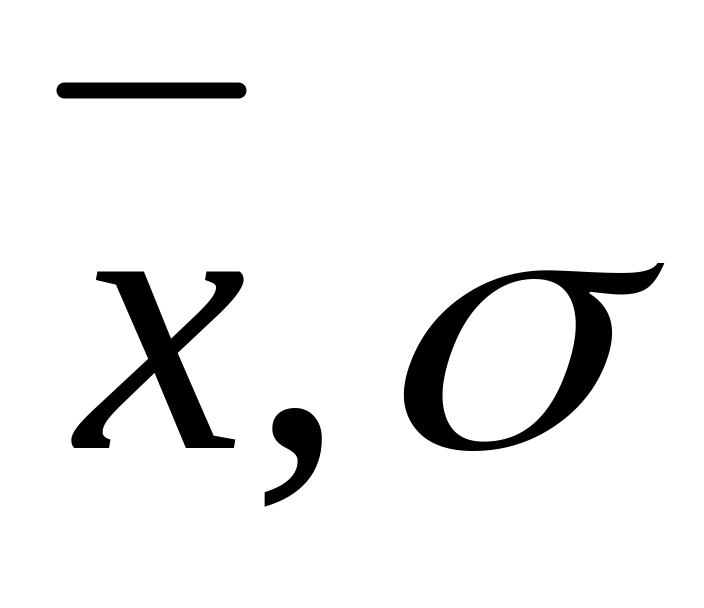7. Если – выборка объема из нормальной генеральной совокупности с параметрами , а 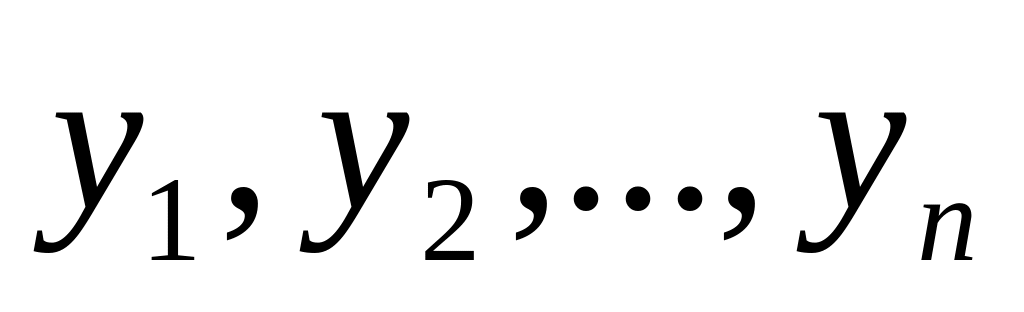– выборка объема совокупности с параметрами 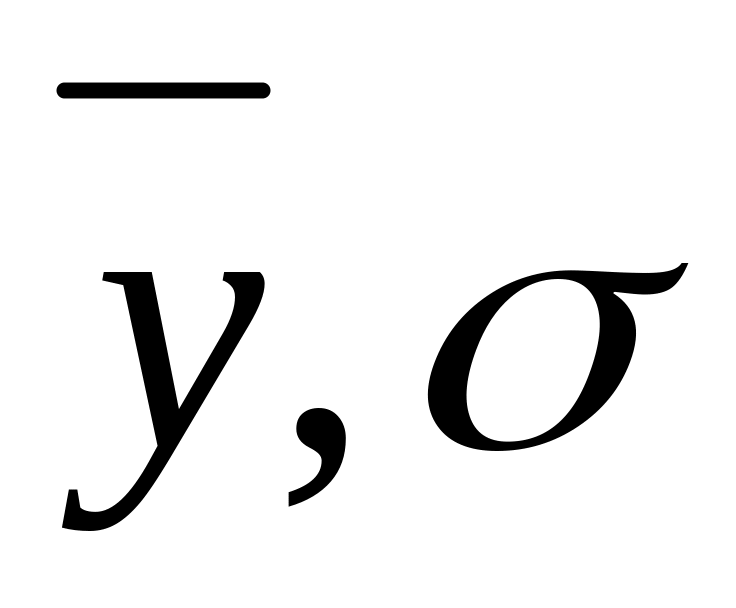, то статистика:

.

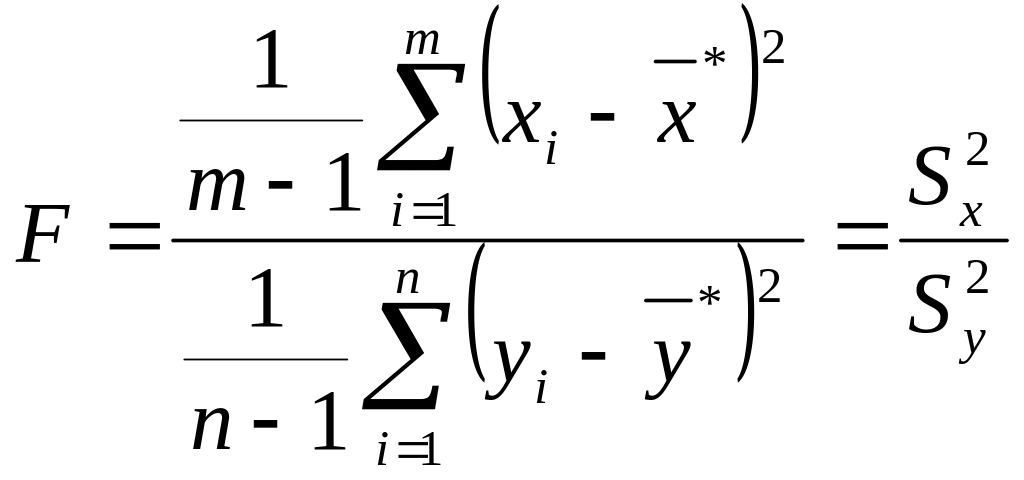имеет F-распределение Фишера-Снедекора с и степенями свободы. (Здесь и – выборочные оценки математических ожиданий и соответственно).
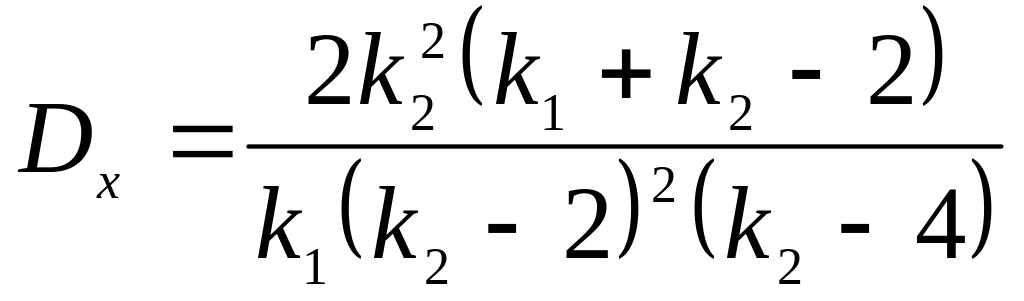
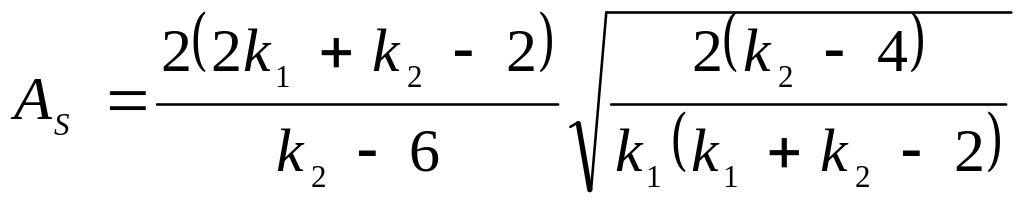
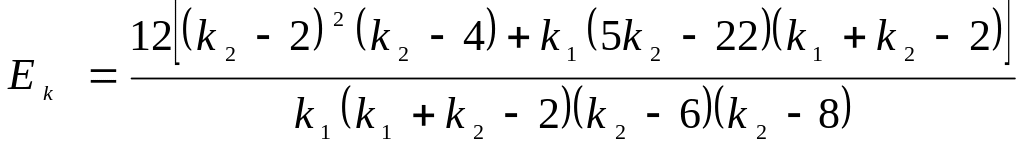
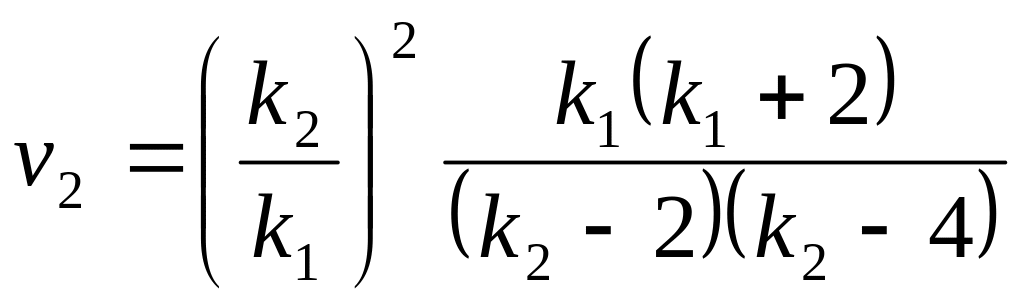
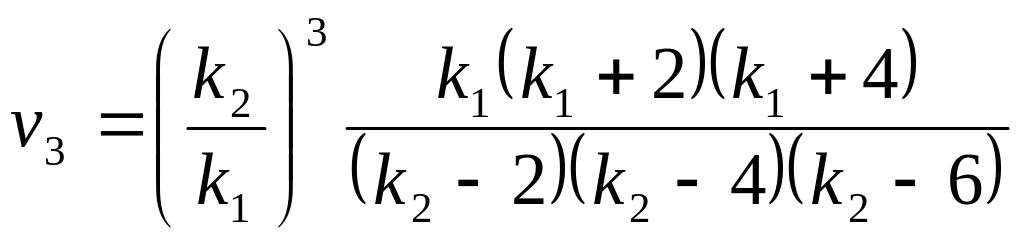
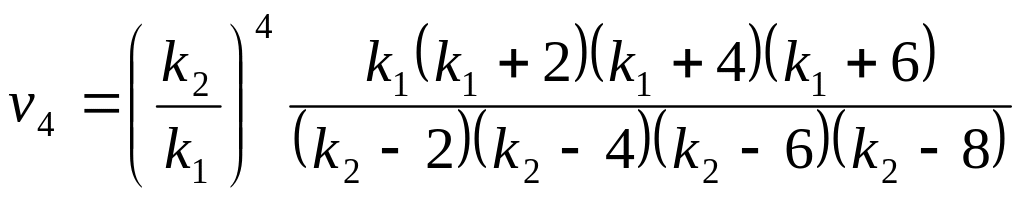
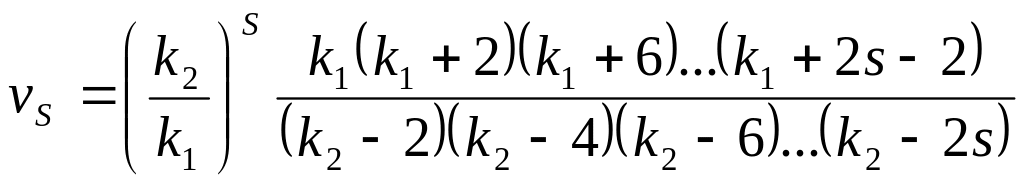
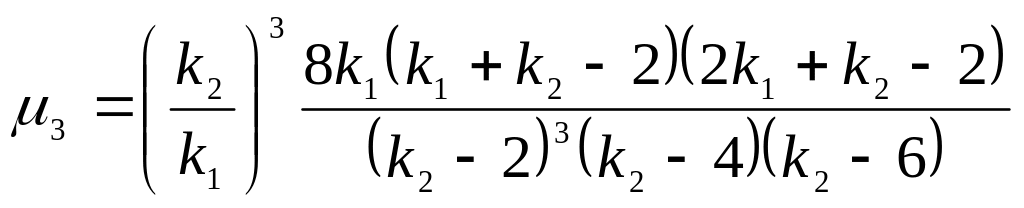
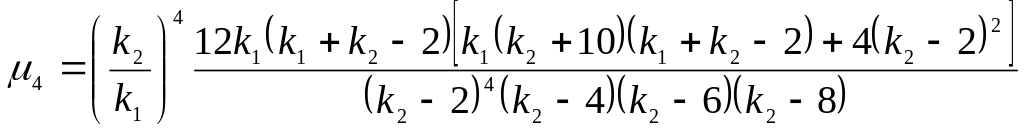