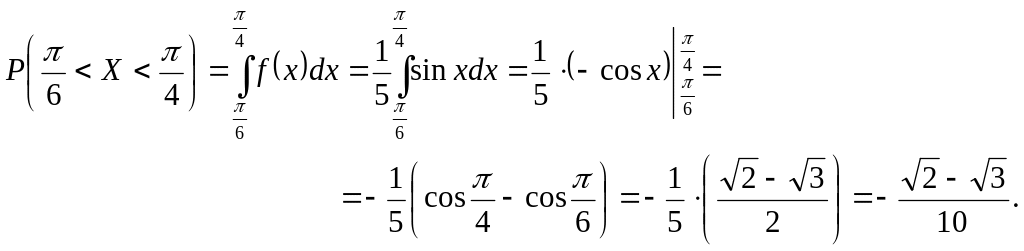- •Предисловие
- •Введение
- •Глава 1. Случайные события § 1.1. Основные понятия теории вероятностей § 1.1.1. Испытания и события. Виды случайных событий
- •§ 1.1.2. Классическое определение вероятности
- •Свойства вероятности
- •§ 1.1.3. Основные формулы комбинаторики
- •§ 1.1.4. Примеры непосредственного вычисления вероятностей
- •§ 1.1.5. Относительная частота
- •§ 1.2. Теорема сложения вероятностей § 1.2.1. Теорема сложения вероятностей несовместных событий
- •§ 1.2.2. Полная группа событий
- •§ 1.2.3. Противоположные события
- •§ 1.3. Теорема умножения вероятностей § 1.3.1. Произведение событий
- •§ 1.3.2. Условная вероятность
- •§ 1.3.3. Теорема умножения вероятностей
- •§ 1.3.4. Независимые события. Теорема умножения для независимых событий
- •§ 1.3.5. Вероятность появления хотя бы одного события
- •§ 1.3.6. Вероятность гипотез. Формулы Бейеса
- •§ 1.3.7. Повторные испытания. Формула Бернулли
- •§ 1.3.8. Теорема Лапласа
- •§ 1.3.9. Производящая функция
- •Глава 2. Случайные величины. Виды случайных величин § 2.1. Случайные величины
- •§ 2.1.1. Дискретные и непрерывные случайные величины
- •§ 2.1.2. Закон распределения вероятностей случайной величины
- •§ 2.1.3. Закон распределения вероятностей дискретной случайной величины
- •§ 2.1.3.1. Биноминальное распределение
- •§ 2.1.3.2. Распределение Пуассона
- •§ 2.1.3.3. Простейший поток событий
- •§ 2.1.3.4. Геометрическое распределение
- •§ 2.1.4. Непрерывные случайные величины. Функция распределения
- •§ 2.2. Закон больших чисел
- •§ 2.3. Математическое ожидание случайной величины
- •§ 2.3.1. Математическое ожидание дискретной случайной величины
- •§ 2.3.2. Математическое ожидание непрерывной случайной величины
- •§ 2.3.3. Основные свойства математического ожидания
- •§ 2.4. Дисперсия случайной величины
- •§ 2.4.1. Отклонения случайной величины от ее математического ожидания
- •§ 2.4.2. Дисперсия дискретной случайной величины
- •§ 2.4.3. Дисперсия непрерывной случайной величины
- •§ 2.4.4. Основные свойства дисперсии
- •§ 2.4.5. Среднее квадратическое отклонение
- •§2.4.6. Начальные и центральные теоретические моменты
- •§ 2.4.7. Асимметрия и эксцесс
- •§ 2.4.8. Функция одного случайного аргумента
- •§2.4.9. Функция двух случайных аргументов
- •§ 2.5. Законы распределения случайных величин
- •§ 2.5.1. Закон равномерного распределения вероятностей
- •Свойства равномерного распределения
- •§ 2.5.2. Нормальное распределение
- •§ 2.5.3. Распределение «хи-квадрат»
- •§ 2.5.4. Распределение Стьюдента
- •§ 2.5.5. Распределение f Фишера-Снедекора
- •§ 2.5.6. Показательное распределение
- •§ 2.5.7. Гамма-распределение и распределение Эрланга
- •Свойства нормированного распределения Эрланга
- •§ 2.5.8. Функция надежности
- •§ 2.6. Система двух случайных величин
- •§ 2.6.1. Закон распределения вероятностей дискретной двумерной случайной величины
- •§ 2.6.2. Функция распределения двумерной случайной величины
- •§ 2.6.3. Вероятность попадания случайной точки в полуполосу
- •§ 2.6.4. Вероятность попадания случайной точки в прямоугольник
- •§ 2.6.5. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины (двумерная плотность вероятности)
- •§ 2.6.6. Нахождение функции распределения системы по известной плотности распределения
- •§ 2.6.7. Условные законы распределения составляющих системы случайных величин
- •1. Система дискретных случайных величин
- •2. Система непрерывных случайных величин
- •§ 2.6.8. Условное математическое ожидание
- •§ 2.6.9. Зависимые и независимые случайные величины
- •§ 2.6.10. Числовые характеристики системы двух случайных величин
- •§ 2.6.11. Коррелированность и зависимость случайных величин
- •§ 2.6.12. Линейная регрессия
- •Глава 3. Примеры для самостоятельной работы
- •Приложения
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения Фишера – Снедекора
- •Равномерно распределенные случайные числа
- •Библиографический список
- •Предметный указатель
- •Оглавление
§ 2.1.4. Непрерывные случайные величины. Функция распределения
Случайную величину
будем называть непрерывной,
если все ее возможные значения целиком
заполняют некоторый конечный или
бесконечный промежуток
![]() числовой оси. Предполагается, что при
каждом испытании случайная величина
принимает одно и только одно значение
числовой оси. Предполагается, что при
каждом испытании случайная величина
принимает одно и только одно значение
![]() .
Заметим, что дискретные и непрерывные
случайные величины не исчерпывают все
типы случайных величин.
.
Заметим, что дискретные и непрерывные
случайные величины не исчерпывают все
типы случайных величин.
Для характеристики непрерывной случайной величины вводят функцию распределения
![]() ,
(3)
,
(3)
называемую интегральным законом распределения.
Если значения
случайной величины
рассматривать как точки числовой оси
![]() ,
то
,
то
![]() представляет собой вероятность события,
состоящего в том, что наблюдаемое
значение случайной величины
принадлежит интервалу
представляет собой вероятность события,
состоящего в том, что наблюдаемое
значение случайной величины
принадлежит интервалу
![]() ,
то есть находится левее точки
.
Этот интервал зависит от правого конца,
и поэтому, естественно, вероятность
является функцией от
,
определенной на оси
,
то есть находится левее точки
.
Этот интервал зависит от правого конца,
и поэтому, естественно, вероятность
является функцией от
,
определенной на оси
![]() .
.
Функцией распределения называют функцию , определяющую для каждого вероятность того, что случайная величина примет значение, меньшее , то есть
![]() .
.
Функция распределения обладает следующими свойствами:
I.
Функция
есть неубывающая функция аргумента
,
то есть если
![]() ,
то
,
то
![]() .
.
II.
Так как
– вероятность, то справедливо неравенство
![]() .
.
III.
![]() .
.
Таким образом,
вероятность того, что случайная величина
примет значение, принадлежащее промежутку
![]() ,
равна приращению ее функции распределения
на этом промежутке.
,
равна приращению ее функции распределения
на этом промежутке.
В дальнейшем
случайную величину
будем называть непрерывной лишь в том
случае, когда ее функция распределения
непрерывна на оси
![]() .
.
Теорема. Вероятность
(до опыта) того, что случайная величина
примет заранее указанное строго
определенное значение
![]() равно нулю.
равно нулю.
Следствие. Для непрерывной случайной величины справедливы равенства:
![]() (4)
(4)
![]() ,
(5)
,
(5)
где
![]() – ее функция распределения.
– ее функция распределения.
Предположим теперь, что для непрерывной случайной величины ее функция распределения имеет непрерывную производную:
![]() .
(6)
.
(6)
Функцию
![]() называют плотностью
вероятности
(для данного распределения) или
дифференциальным
законом распределения
случайной величины
.
называют плотностью
вероятности
(для данного распределения) или
дифференциальным
законом распределения
случайной величины
.
Заметим, что плотность вероятности представляет собой отношение вероятности попадания точки в бесконечно малый промежуток к длине этого промежутка [5].
Так как плотность
вероятности
является производной неубывающей
функции
,
то она неотрицательна:
![]() .
В отличие от вероятности, плотность
вероятности может принимать сколь
угодно большие значения.
.
В отличие от вероятности, плотность
вероятности может принимать сколь
угодно большие значения.
Так как является первообразной для , то на основании формулы Ньютона-Лейбница имеем:
![]() .
.
Отсюда получаем
![]() .
(7)
.
(7)
Геометрически
(рис.1) эта вероятность представляет
собой площадь
криволинейной трапеции, ограниченной
графиком плотности вероятности
![]() ,
осью
и двумя ординатами
,
осью
и двумя ординатами
![]() и
и
![]() .
.

![]()
Рис.1. Геометрическое представление плотности распределения
Полагая
![]() и
и
![]() ,
получаем достоверное событие
,
получаем достоверное событие
![]() ,
вероятность которого равна единице.
Следовательно,
,
вероятность которого равна единице.
Следовательно,
![]() .
(8)
.
(8)
Полагая в формуле
(4)
,
![]() и обозначая для ясности переменную
интегрирования
другой буквой, например
(это законно для определенного интеграла),
получаем функцию
распределения:
и обозначая для ясности переменную
интегрирования
другой буквой, например
(это законно для определенного интеграла),
получаем функцию
распределения:
![]() .
(9)
.
(9)
Пример 2.10. Дискретная случайная величина задана таблицей распределения (табл. 5):
Таблица 5
|
1 |
3 |
9 |
|
0,2 |
0,7 |
0,1 |
Найти функцию распределения и построить ее график.
Решение. Если
![]() ,
то
,
то
![]() (по свойству функции распределения).
(по свойству функции распределения).
Если
![]() ,
то
,
то
![]() ,
так как
может принимать только значение 1 с
вероятностью 0,2.
,
так как
может принимать только значение 1 с
вероятностью 0,2.
Если
![]() ,
то
,
то
![]() .
.
Так как может принять значение 1 с вероятностью 0,2 и значение 3 с вероятностью 0,7, следовательно, по теореме сложения вероятностей несовместных событий .
Если
![]() ,
то
,
то
![]() .
.
Итак, искомая функция распределения имеет вид
![]()
График этой функции представлен на рис.2.

Рис.2. График функции распределения
Пример 2.11.
Непрерывная случайная величина
задана плотностью распределения
![]() в интервале
в интервале
![]() ;
вне этого интервала
;
вне этого интервала
![]() .
Найти вероятность того, что
примет значение, принадлежащее интервалу
.
Найти вероятность того, что
примет значение, принадлежащее интервалу
![]() .
.
Решение. Вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу , определяется равенством