§ 2.1.3.3. Простейший поток событий

Рассмотрим события, которые наступают в случайные моменты времени.

Потоком событий называют последовательности событий, которые наступают в случайные моменты времени.

Примерами потоков служат: поступление вызовов на АТС, на пункты неотложной помощи, клиентов на предприятие и т.д. [3].

Простейшим (пуассоновским) называют поток событий, который обладает свойствами: стационарностью, «отсутствием последействия» и ординарностью.

1. Свойство стационарности состоим в том, что вероятность появления событий на любом промежутке времени зависит только от числа и от длительности 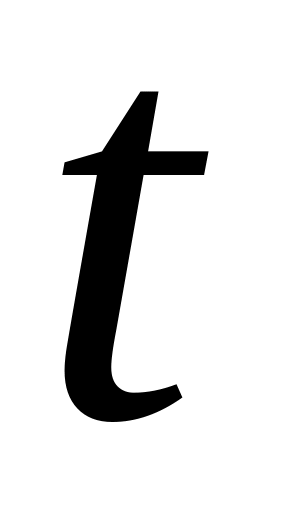промежутка и не зависит от начала его отсчета; при этом различные промежутки времени предполагаются непересекающимися.

Итак, если поток обладает свойством стационарности, то вероятность появления событий за промежуток времени длительности есть функция, зависящая только от и .

2. Свойство «отсутствия последействия» характеризуется тем, что вероятность появления событий на любом промежутке времени не зависит от того, появились или не появились события в моменты времени, предшествующие началу рассматриваемого промежутка. Таким образом, предыстория потоков не сказывается на вероятности появления событий в ближайшем будущем.

Итак, если поток обладает свойством отсутствия последействия, то имеет место взаимная независимость появлений того или иного числа событий в непересекающиеся промежутки времени.

3. Свойство ординарности характеризуется тем, что появление двух и более событий за малый промежуток времени практически невозможно.

Итак, если поток обладает свойством ординарности, то за бесконечно малый промежуток времени может появиться не более одного события.

Интенсивностью потока называется среднее число событий, которые появляются в единицу времени.

Если постоянная интенсивность потока известна, то вероятность появления событий простейшего потока за время - определяется формулой Пуассона:

– математическая модель простейшего потока событий.

Пример 2.8. Среднее число заказов такси, поступающих на диспетчерский пункт в одну минуту, равно четырем. Найти вероятность того, что за две минуты поступит менее 6 вызовов.

Решение. По условию , событие «поступило менее 6 вызовов», произойдет, если наступит одно из следующих несовместных событий:

1. поступило 5 вызовов,

2. поступило 4 вызова,

3. поступило 3 вызова,

4. поступило 2 вызова,

5. поступил 1 вызов,

6. не поступило ни одного вызова.

Эти события несовместны, поэтому применима теорема сложения вероятностей несовместных событий:

.

Вычислим . По условию .

Воспользуемся формулой Пуассона: .

Тогда

.

§ 2.1.3.4. Геометрическое распределение

Пусть производятся независимые испытания, в каждом из которых вероятность появления события равна и вероятность его непоявления .

Испытания заканчиваются, как только появится событие . Таким образом, если событие появилось в -м испытании, то в предшествующих испытаниях оно не появлялось.

Обозначим через дискретную случайную величину – число испытаний, которые нужно провести до первого появления события .

Вероятность того, что в -м испытании появилось событие , применив теорему умножения вероятностей, равна ,

где , то есть

. (2)

Полагая , получим соответствующую геометрическую прогрессию с первым членом и знаменателем ( )

По этой причине распределение (1) называется геометрическим.

Пример 2.9. Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель .

Найти вероятность того, что попадание произойдет при третьем выстреле.

Решение. Так как , , то ; искомая вероятность

.