33. Дії над матрицями.

Дія 1. Операція додавання матриць вводиться тільки для матриць однакових розмірів. Сумою С=А+В називається матриця С, кожен елемент якої є сума елементів матриць А і В.

Дія 2. Добутком матриці А на число к називається матриця В=к*А.

Дія 3. Різниця матриць А-В визначається як сума матриці А і матриці В помноженої на (-1).

Справедливі такі властивості операцій:

1. А+В=В+А (комутативний закон)

2. А+В+С=(А+В)+С (асоціативний закон)

3. А+0=А; А-А=0

4. *(А)=(*)*А – де  і  - просто числа

5. (А+В)= А+В

6. (+)А=А+А

Дія 4. Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В. Якщо ця умова не виконується, то множення матриць неможливе.

Добутком С=А*В називається матриця, кожен елемент якої С_ij дорівнює сумі добутків елементів і-того рядка матриці А на відповідні елементи j-того стовпця матриці В.

Операція матриць не комутативна А*ВВ*А.

Одинична матриця має чудову властивість: добуток одиничної матриці на квадратну матрицю дорівнює цій квадратній матриці.

34. Обернена матриця

Матриця називається оберненою, якщо в результаті множення її на вихідну матрицю (як зліва, так і справа) утворюється одинична матриця: А*А^-1= А^-1*А=Е

(Нехай квадратна матриця, матриця А^-1 називається оберненою до матриці А, якщо виконується умова А*А^-1= А^-1*А=Е.)

Квадратна матриця називається виродженою, якщо детермінант detA=0, і не виродженою, якщо detA0.

Якщо А=

Обернена матриця існує тільки для не вироджених матриць.

А_ij – алгебраїчні доповнення до елементів а_ij визначника detA.

35. Матричний запис лінійних рівнянь.

Розглянемо систему рівнянь:

Введемо позначення

Матриця А складена з коефіцієнтів системи (1) називається основною матрицею системи..

Матриця Х складена з невідомих і називається матрицею невідомих.

Матриця В називається матрицею вільних членів.

Тоді, згідно з правилами множення матриць, систему (1) запишемо в матричному вигляді А*Х=В (2)

Припустимо, що матриця А системи (1) не вироджена і має обернену матрицю А^-1. Помножимо рівність (2) на А^-1 зліва

А^-1 *А*Х= А^-1*В, де А^-1 *А=Е.

Е*Х= А^-1 *В, звідси Х= А^-1 *В.

36. Критерії сумісності системи лінійних рівнянь. Теорема Кронекера -Капеллі.

Вичерпну відповідь на запитання про існування розв’язку системи m лінійних рівнянь з n невідомими дає теорема Кронекера-Капеллі.

Теорема: Для того, щоб система лінійних рівнянь була сумісною, необхідно і достатньо, щоб ранг її основної матриці дорівнював рангу розширеної.

Якщо ранг основної матриці дорівнює рангу розширеної і дорівнює числу невідомих, то система має єдиний розв’язок.

Якщо ранг основної матриці дорівнює рангу розширеної матриці, але менше числа невідомих, то система має безліч розв’язків.

37. Означення

49.Коротко означення границы можна записати так:

( >0 N=N( ) : n>N < ) = x₀ ,

Розглянемо геометричний зміст границі послідовності:

Нерівність < рівносильна нерівностям – < < , або - < < + , які

Показують, що елемент знаходиться в -околі точки .Тому означення границі геометрично можна сформулювати так: число наз.границею послідовності ,якщо для довільного -окола точки існує такий номер N=N( ),що всі значення , для яких n>N, попадають в цей окіл. Поза цим може залишитися хіба що скінчена кількість членів послідовності .

5 0. у=f(x)

В

А мал.(1)

Нехай функція у=f(x) мал.(1) визначена в деякому околі точки x_0. Число А наз. границею функції у=f(x) зліва в точці x_0, якщо для будь-якого числа >0 існує число = ( )>0 таке, що при х (x₀ – ; x₀) виконується нерівність < .

Число B наз. границею функції у=f(x) справа в точці x_0, якщо для будь-якого числа >0 існує число = ( )>0 таке, що при х (x_0; x₀ + ;) виконується нерівність < .

Ліву і праву границі функції мал.(1) називають односторонніми границями.

Необхідна і достатня умова існування границі функції в точці:

Умова f(x₀ +0)=f(x₀ -0) є необхідною і достатньою для існування границі функції у=f(x) в точці x₀: (f(x₀+0)=f(x₀-0)=A) .

№53

Перша чудова границя:

При знаходжені границі виразів що містять тригонометричні функції було виведено

Наслідки з першої чудової границі

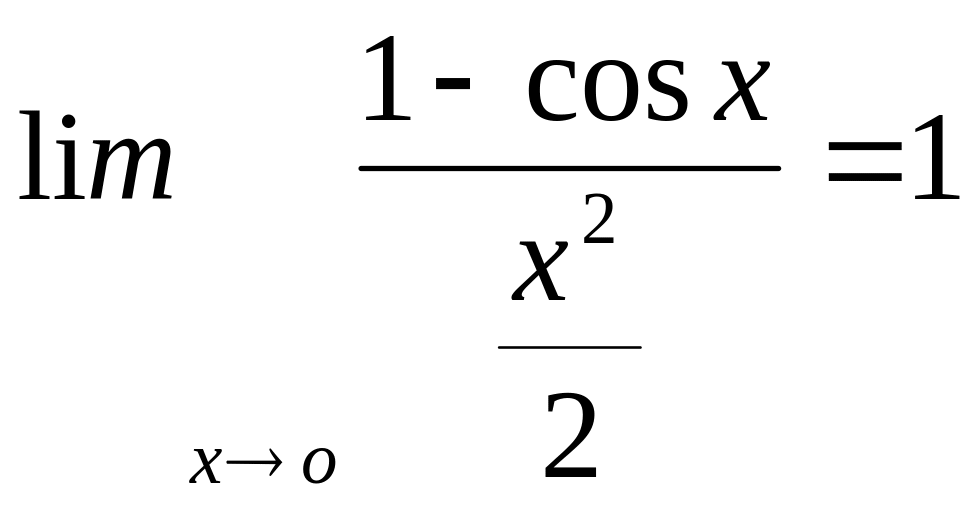
Друга чудова границя

Її наслідки

№54

Нехай функція f(x) визначена в точці і даному околі цієї точки функція f(x) називається неперервною якщо її значення дорівнює 0.

Можна дати ще одне означення неперервності функції опираючись на поняття приростів аргументу. Якщо нескінченно малому прирісту аргументу х в точці х = х0 відповідає нескінченно малий приріст у функції, що визначена в точці х0 та в її околі, то функцію у = (х) нази¬вають неперервною при х = х0 або в точці х0.

Різниця х-х0 називається приростом аргументу в т. х0

Різниця відповідних значень функції f(x)-f(x0) називається приростом функції в т. х0.

- попарно ортогональні орти, то ²= ²= ²=1,

· = = · =0, тому · = а_хb_x + a_yb_y + a_zb_z .

Отже, скалярний добуток двох векторів, заданих координатами в прямокутній системі координат, дорівнює сумі добутків їхніх відповідних координат.

Висновки з отриманого:

а_хb_x + a_yb_y + a_zb_z=0- умова перпендикулярності векторів.