19.Лінійні операції над векторами, властивості лінійних операцій над векторами.

20.Означення і основні властивості скалярного добутку.

Скалярним добутком двох векторів називається число ab, що дорівнює добутку довжин векторів a i b на cos між ними.

Властивості скалярного добутку:

1)Комунікативна властивість множення ,тобто

2)Асоціативна властивість відносно множення на число .

3)Дистрибутивна властивість відносно додавання векторів .

4)Якщо вектор

5)Скалярний добуток двох не нульових векторів =0 тоді і лише тоді,коли ці вектори перпендикулярні .

6)Скалярний квадрат вектора = квадрату його довжин.

21.Вираження скалярного добутку за допомогою координат.

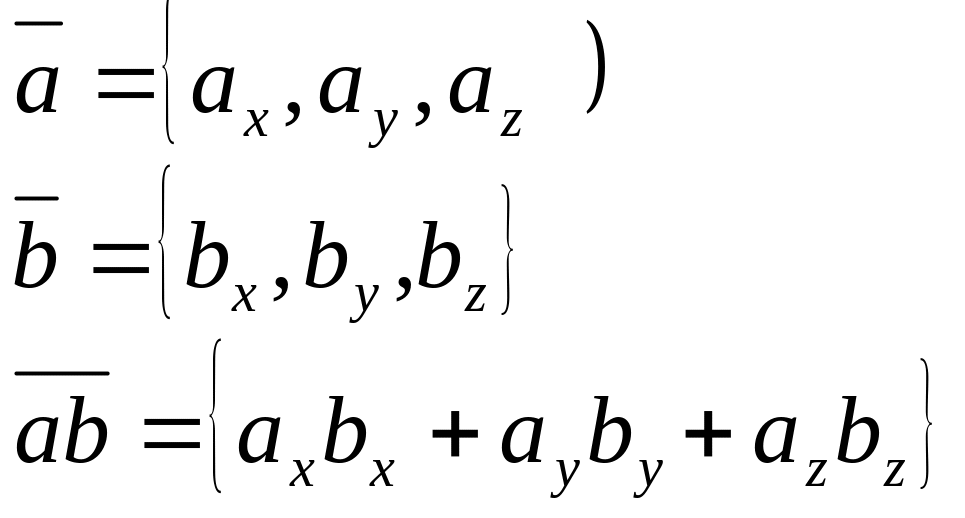
Необхідною і достатньою умовою перпендикулярності двох векторів є рівність 0 їх скалярного добутку.

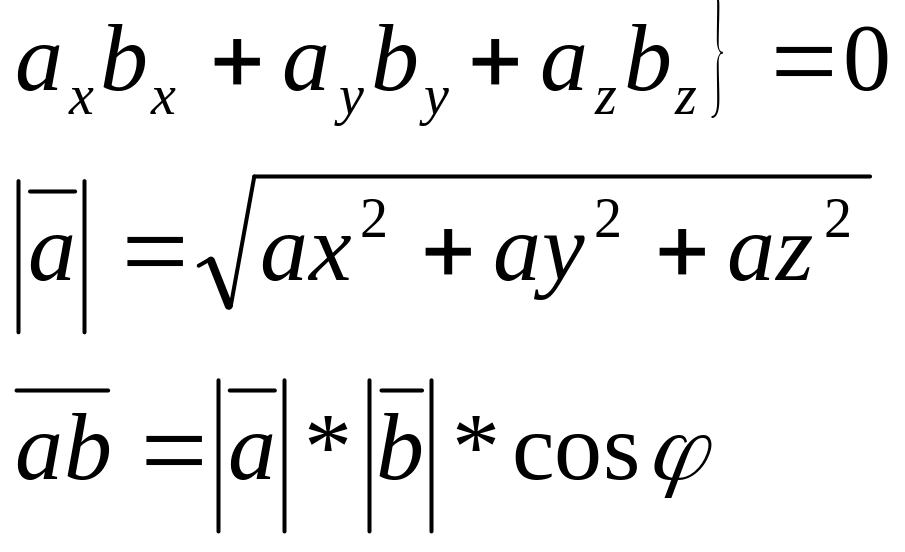
22.Вектрний добуток векторів.Властивості

векторного добутку.Вираження векторного добутку векторів через їх координати. вектора на вектор

наз. вектор , який визначається 3 умовами:

1.Довжина вектора = , де ϕ- кут між векторами;

2.Вектор перпендикулярний до кожного з векторів і ;

3.Якщо ≠0, то вектори , і утворюють праву трійку векторів.

Алгебраїчні властивості векторного добутку:

1.Антикомутативність:

х = -( х )

2.Асоціативність відносно скалярного множника :

х = ( х )

3.Дистрибутивність відносно додавання векторів:

х( + )= х + х

Геометричні властивості:

4.Векторний добуток дорівнює нулю тоді і тільки тоді, коли вектори колінеарні;

5.Модуль векторного добутку неколінеарних векторів дорівнює площі пар-грама, побудованого на векторах і , віднесених до спільного початку, тобто S= .

6.Векторні добутки ортів задовольняють такі рівності:

х = х = х =0; х = _, х = , х = .

Вираження векторного добутку векторів через їх координати:

Нехай задано два вектори ={a_x ; a_y ; a_z} та ={b_x ; b_y ; b_z}. Векторний добуток вектора на вектор визначається за формулою (1) та виражається через іх координати:

х =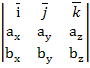 (1).

х =(а_х +а_у +а_z ) ·(b_х +b_у +b_z ) = а_хb_x( х ) + а_хb_y( х )+ a_x b_z( х ) + a_y b_x ( х ) + а_yb_y( х )+

+a_yb_z( х ) + a_z b_x( х ) +a_z b_y( х ) + a_zb_z( х )=( a_yb_z – a_zb_y) – (a_xb_z – a_zb_x) + (а_хb_y - a_y b_x)=

= .

23.Мішаний добуток трьох векторів і його властивості. Вираження мішаного добутку через координати векторів.Умова компланарності трьох векторів.

24. Загальне рівняння площини та його дослідження

25. Рівняння пдощини,що проходить через 3 точки.Рівняння площини у відрізках на осях.

Нехай на площині П задано три точки:

M1(x1,y1,z1)

M2(x2,y2,z2)

M3(x3,y3,z3),які не лежать на одній прямій ці точки однозначно визначають площину

Знайдемо її рівняння.Візьмемо на площині довільну т.M(x,y,z) і знайдемо

M1M={x-x1;y-y1;z-z1}

M1M2{x2-x1;y2-y1;z2-z1}

M1M3{x3-x1;y3-y1;z3-z1},де M1M,M1M2,M1,M3(вектори),

ці вектори лежать в площині π,тобто вони компланарні.Оскільки мішаний добуток

компланарних векторів=0,то

|x-x1 y-y1 z-z1|

det |x2-x1 y2-y1 z2-z1|=0 (зірочка)

|x3-x1 y3-y1 z3-z1|

Це рівняння площини,що проходить через 3 точки.

Нехай площина відтинає на осях

ox,oy,oz відрізки a,b,c A(a,0,0) ,B(0,b,0) ,C(0,0,C).Підстівляючи ці точки в рівняння

зірочка дістанемо рівняння:

x/a+y/b+z/c=1 – рівняння площини у відрізках на осях.