1. Метод координат. Положення точки на прямій.

Декарт, який був основоположником, що вперше в 1637 році у своїй книзі «Геометрія» дав чіткий виклад ідеї методу координат на площині. Він запропонував положення точки на площині відносно заданої системи координат визначати за допомогою двох чисел – її координат. А кожну лінію на площині розглядати як множину точок, заданих першою геометричною умовою. Ця умова записується у вигляді рівняння, яке зв’язує змінні координати точок, що належать даній лінії і називається рівнянням цієї лінії. Такий спосіб дослідження геометричних об’єктів і називається методом координат.

2. Прямокутна система координат на площині.

Будемо вважати, що на площині задана Декартові прямокутна система координат, якщо заданий одиничний (масштабний) відрізок, а також пара взаємно перпендикулярних осей і при цьому домовлено, яка з осей є першою, а яка другою. Точку О перетину цих осей будемо називати початком координат, першу з осей віссю абсцис або віссю Ох, другу – віссю ординат або віссю Оу.

В довільній точці площини М поставимо у відповідність два числа:

- абсцису х, що дорівнює відстані точки М від осі Оу, взятій зі знаком «+», якщо точка М лежить праворуч Оу, і зі знаком «-», якщо ліворуч;

- ординату у, що дорівнює відстані точки М від осі Ох, взятій зі знаком «+», якщо М лежить вище Ох, і зі знаком «-», якщо нижче осі Ох.

Абсциса х і ордината у називаються декартовими прямокутними координатами точки М (х;у).

Кожній точці площини відповідає одна пара дійсних чисел (х;у) і навпаки, кожній парі дійсних чисел х і у відповідає одна точка площини. Координатні вісі Ох і Оу розбивають площину на 4 квадрати. Відповідно знаки:

В 1 – «+», «+» В 2 – «+»

В 3 – «-», «-» В 4 «+», «-».

3. Відстань між двома точками на площині.

Згідно з теоремою Піфагора це:

D=M₁M₂=

4. Поділ відрізка у заданому відношенні.

Нехай на площині задано 2 точки. Необхідно знайти точку М (х;у), що лежить на відрізку М₁М₂ і ділить його у відношенні . З елементарної геометрії можна записати що

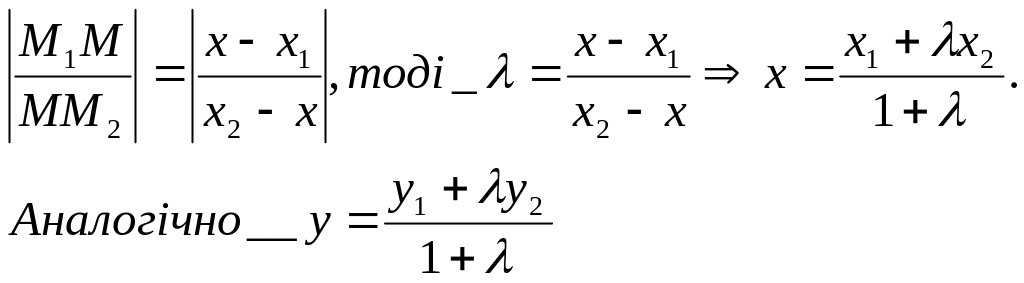
Якщо і т.М ділить відрізок навпіл.

5. Полярні координати. Залежність між прямокутними і полярними координатами.

Зафіксуємо на площині точку О і напівпряму ОР, яка виходить з цієї точки, а також виберемо одиницю масштабу. Точка О називається полюсом , ОР – полярною віссю. В довільній точці М площини поставимо у відповідність 2 числа:

1) полярний радіус , що дорівнює відстані точки М від полюсу О, виміряний обраною одиницею масштабу;

2) Полярний кут , рівний кутові між полярною віссю ОР і напівпрямою ОМ. Кут  вимірюється в радіанах. Відлік додатніх значень  ведеться від ОР проти руху годинникової стрілки -. Запис М(,) має полярні координати  і .

Якщо полюс полярної системи координат помістити в початок прямокутної системи координат так, щоб полярна вісь збіглась з віссю Ох, то легко встановити залежність між полярними і прямокутними координатами.

Звідси

У виразі tg= можна одержати два значення полярного кута  тому, що -. Тому при обчисленні  для точки М за її прямокутними координатами, спочатку з’ясовують, в якому квадраті вона знаходиться.