
- •Теоретическая часть
- •Теоретическая часть
- •Теоретическая часть
- •Теоретическая часть
- •Элементы комбинаторики
- •Классическая вероятность
- •Некто, перетасовывая колоду из 36 карт, извлекает оттуда случайным образом одну карту. Какова вероятность того, что это будет туз?
- •В конверте среди 25 карточек находится разыскиваемая карточка. Из конверта наудачу извлечено 6 карточек. Какова вероятность, что среди них окажется нужная карточка?
- •Вычисление вероятностей с помощью формул комбинаторики
- •Теоретическая часть
- •Теоретическая часть Вычисление вероятностей независимых событий
- •Теоретическая часть Тема "Дискретные случайные величины"
- •Числовые характеристики дискретных случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии
- •Теоретическая часть
Тема: «Вычисление предела функции»
Теоретическая часть
Правила вычисления предела функции на бесконечности
П![]() равило
1.
Для любого натурального показателя m
и любого коэффициента k
справедливо соотношение:
равило
1.
Для любого натурального показателя m
и любого коэффициента k
справедливо соотношение:
![]()
![]() Правило
2.
Если
, , то
Правило
2.
Если
, , то
![]()
Предел суммы равен сумме пределов:
![]()
Предел произведения равен произведению пределов:
![]()
Предел частного равен частному пределов (если с≠0):
![]()
Постоянный множитель можно вынести за знак предела:
![]()
Пример 1. Вычислите
Р
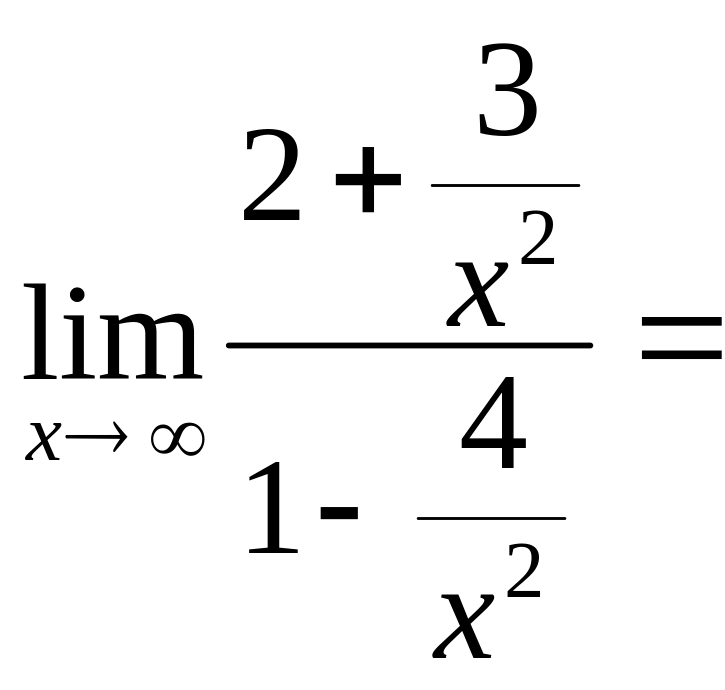
 ешение:
ешение:
![]()
![]()
![]()
Определение.
Ф![]() ункцию
y= f (x) называют непрерывной
в точке x=a, если выполняется соотношение
ункцию
y= f (x) называют непрерывной
в точке x=a, если выполняется соотношение
Если выражение f (x) составлено из рациональных, иррациональных, тригонометрических и обратных тригонометрических выражений, то функция y= f (x) непрерывна в любой точке, в которой определено выражение f (x)
![]()
Пример 2. Вычислить
Решение:
В![]()
![]() ыражение
определено в любой точке
x, в частности в точке x=1. Следовательно,
функция непрерывна в
точке x=1, а поэтому предел функции при
стремлении x к 1 равен значению функции
в точке x=1:
ыражение
определено в любой точке
x, в частности в точке x=1. Следовательно,
функция непрерывна в
точке x=1, а поэтому предел функции при
стремлении x к 1 равен значению функции
в точке x=1:
![]()
П![]() ример
3. Вычислить
ример
3. Вычислить
Решение:
![]()
![]()
![]()
![]()
Пример 4. Вычислить
Решение:
Ф![]() ункция
в точке x=-3
не определена. Поэтому числитель и
знаменатель надо разложить на множители:
ункция
в точке x=-3
не определена. Поэтому числитель и
знаменатель надо разложить на множители:
![]()
![]()
![]()
Пример
5. Вычислить![]()
Решение:

Замечательные пределы
Пример
6. Вычислить
![]()
Решение:
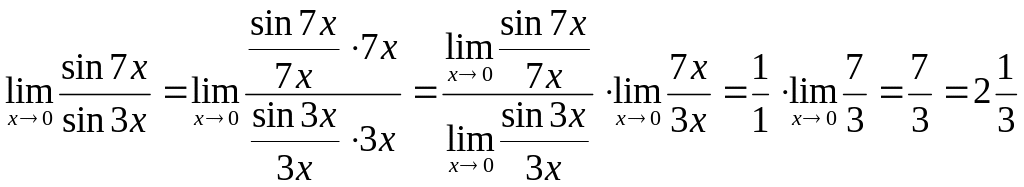
Тема: «Вычисление производной функции»
Теоретическая часть
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила дифференцирования:

 ,
где С - число
,
где С - число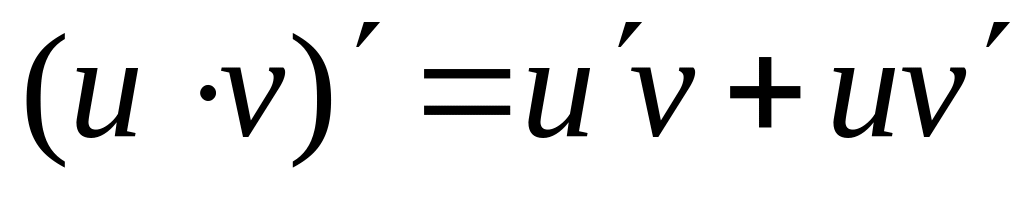

Производная
сложной функции:
![]()
Пример
1 . Найти производную функции
![]()
Решение: Пользуясь правилами дифференцирования и таблицей производных, получим:
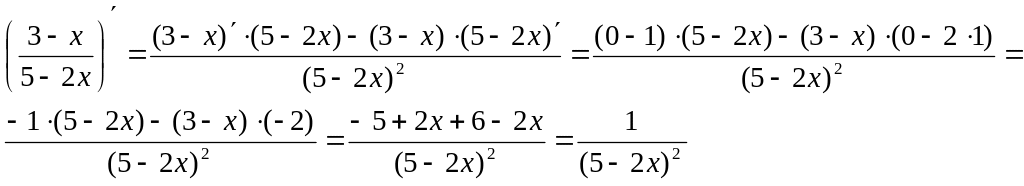 Пример
2 . Найти производную функции
Пример
2 . Найти производную функции
![]()
Воспользуемся формулой производной сложной функции:
![]() .
.
Пример
3
. Найти производную функции
![]()
Решение:
![]() .
.
Тема: «Условия монотонности функции. Необходимое и достаточное условие экстремума»
Теоретическая часть
Пример 1:
Пример
2: Найти экстремум функции
![]() .
.
Найдем
производную функции. Она равна
![]() .
Приравниваем производную к нулю
.
Приравниваем производную к нулю
![]() и находим критическую точку
и находим критическую точку
![]() .
Чтобы найти ординату этой точки, подставим
в данную функцию
.
Чтобы найти ординату этой точки, подставим
в данную функцию
![]() и запишем вершину параболы C(1; 4). Ось
симметрии проходит через C параллельно
оси
и запишем вершину параболы C(1; 4). Ось
симметрии проходит через C параллельно
оси
![]() (рис. 3). Пересечение параболы с осью
:
(рис. 3). Пересечение параболы с осью
:
![]() ;
;
![]() ,
т.е. A(0; 5). Симметричная ей точка A1(2; 5).
,
т.е. A(0; 5). Симметричная ей точка A1(2; 5).
Пример
3: Найти точки экстремума и интервалы
монотонности функции
![]() .
.
Находим первую производную:
![]() и
приравниваем ее к нулю
и
приравниваем ее к нулю
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() и
.
Критическая точка
делит
и
.
Критическая точка
делит
![]() на два интервала монотонности,
при переходе через точку
на два интервала монотонности,
при переходе через точку
![]() меняет знак с
меняет знак с
![]() на
на
![]() .
Следовательно,
- точка минимума.
.
Следовательно,
- точка минимума.
Тема: «Исследование функции одной переменной и построение графика. Асимптоты графика функции»
Теоретическая часть
Схема исследования функций:
Найти область определения функции.
Установить, не является ли функция четной, нечетной, периодической.
Найти точки разрыва и исследовать пределы функции в этих точках.
Найти точки экстремума и значения функции в этих точках.
Исследовать интервалы возрастания и убывания функции.
Для
исследования функции на возрастание и
убывание находят производную ƒ΄(х)
функции ƒ(х) определяют ее знак. (Если
ƒ΄(х)
![]() 0, то ƒ(х) возрастает; если ƒ΄(х)
0, то ƒ(х) возрастает; если ƒ΄(х)
![]() 0, то ƒ(х) убывает)
0, то ƒ(х) убывает)
Найти точки перегиба.
Исследовать график функции на выпуклость и вогнутость (f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.)
Найти точки пересечения с осями координат.
Определить промежутки знакопостоянства функции, т.е. промежутки, на которых ƒ(х) 0 и ƒ(х) 0.
Построить график заданной функции.
Пример
1.
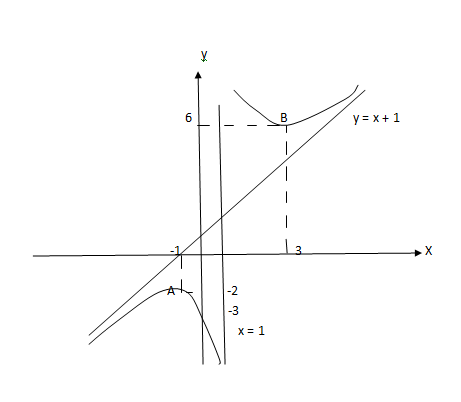
Исследовать
функцию у = ![]() и построить ее график.
Решение.
Область определения функции – вся
числовая ось, кроме точки х = 1,
поэтому, D(у)
= (-
и построить ее график.
Решение.
Область определения функции – вся
числовая ось, кроме точки х = 1,
поэтому, D(у)
= (-![]() 1)
1)
![]() (1; +
(1; +![]() ).
* Так как у (-х) =
).
* Так как у (-х) = ![]() = -
, то функция ни четная и ни нечетная.
* Так как у(х + Т) =
= -
, то функция ни четная и ни нечетная.
* Так как у(х + Т) = ![]() =
= ![]() ни при каком Т
ни при каком Т ![]() 0,
то данная функция не периодическая.
* Строим прямую х = 1. В случае,
когда х приближается к 1 слева, значения
функции стремятся к –
,
а в случае, когда х приближается к
1 справа, значения функции
стремятся к +
.
Так как у =
0,
то данная функция не периодическая.
* Строим прямую х = 1. В случае,
когда х приближается к 1 слева, значения
функции стремятся к –
,
а в случае, когда х приближается к
1 справа, значения функции
стремятся к +
.
Так как у = ![]() +
+ ![]() = х + 1 +
, то при |х|
= х + 1 +
, то при |х| ![]() график этой функции приближается к
графику функции у1
= х
+1.
*
Находим производную у΄
=
график этой функции приближается к
графику функции у1
= х
+1.
*
Находим производную у΄
= ![]() =
= ![]() и
из уравнения
и
из уравнения ![]() -
2х – 3 = 0 определяем критические точки:
х1
= - 1 и х2
= 3. Так как для точек интервала ( -
;
- 1) производная имеет знак «+», а для
точек интервала ( - 1; 1) производная имеет
знак «-», то точка х1
= -1 является точкой максимума функции.
Аналогично убеждаемся, что точка х2
= 3 является точкой минимума функции.
* Так как уравнение х2
+ 3 = 0 не имеет действительных корней,
то
график функции не пересекает ось 0х.
*
На интервале (-
;
- 1) функция возрастает, на интервале (
- 1; 1) – убывает, на
интервале (1; 3) вновь убывает, на интервале
(3; +
)
– возрастает.
Найдем точки графика при х1
= - 1 и х2
= 3; А ( - 1; - 2); В (3; 6).
* Найдем точки пересечения графика
функции с осью 0у: у(0) = - 3.
*
Построим график исходной функции.
-
2х – 3 = 0 определяем критические точки:
х1
= - 1 и х2
= 3. Так как для точек интервала ( -
;
- 1) производная имеет знак «+», а для
точек интервала ( - 1; 1) производная имеет
знак «-», то точка х1
= -1 является точкой максимума функции.
Аналогично убеждаемся, что точка х2
= 3 является точкой минимума функции.
* Так как уравнение х2
+ 3 = 0 не имеет действительных корней,
то
график функции не пересекает ось 0х.
*
На интервале (-
;
- 1) функция возрастает, на интервале (
- 1; 1) – убывает, на
интервале (1; 3) вновь убывает, на интервале
(3; +
)
– возрастает.
Найдем точки графика при х1
= - 1 и х2
= 3; А ( - 1; - 2); В (3; 6).
* Найдем точки пересечения графика
функции с осью 0у: у(0) = - 3.
*
Построим график исходной функции.
Тема: «Вычисление неопределенных интегралов»
Теоретическая часть
Неопределенный
интеграл
функции у = f(х)
– это совокупность всех первообразных
функций F(х)
+ С для функции
f(х).
Обозначается символом ![]() =
F(х)
+ С,
где
=
F(х)
+ С,
где ![]() знак
интеграла;
f(х)
– подынтегральная
функция; f(х)
dх
– подынтегральное
выражение;
С – постоянная
интегрирования,
способная принимать любое значение;
х – переменная интегрирования.
знак
интеграла;
f(х)
– подынтегральная
функция; f(х)
dх
– подынтегральное
выражение;
С – постоянная
интегрирования,
способная принимать любое значение;
х – переменная интегрирования.
Интегрирование – это отыскание первообразной по ее производной. Это действие, обратное дифференцированию.
Геометрический смысл неопределенного интеграла: это семейство кривых, зависящих от одного параметра С, которые получаются путем параллельного переноса вдоль оси 0у.
 у
у


 С1
Кубическая
парабола у =
С1
Кубическая
парабола у = ![]() dх
=
dх
= ![]() + С;
+ С;
С2 0 х
С3
Основные свойства неопределенного интеграла
d
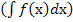 = f(х)
+ С.
= f(х)
+ С.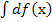 = f(х)
+ С.
= f(х)
+ С. = С
= С 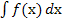 – постоянный множитель можно выносить
за знак интеграла.
– постоянный множитель можно выносить
за знак интеграла. =
+
=
+ 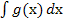 - интеграл суммы равен
сумме интегралов.
- интеграл суммы равен
сумме интегралов.
Основные способы интегрирования
Метод непосредственного интегрирования, который заключается в использовании основных свойств неопределенного интеграла и приведении подынтегрального выражения к табличному виду.
Пример
1.
Найти неопределенный интеграл ![]() .
.
Решение.
Используя 3 и 4 свойства неопределенного
интеграла и таблицу интегрирования,
получаем (таблица прилагается)
= 3 ![]() + 2
+ 2 ![]() = 3
= 3 ![]() -
2cоs
х + С.
-
2cоs
х + С.
Метод подстановки или метод введения новой переменной.
Это самый эффективный прием сведения неопределенного интеграла к табличному виду.
Пример
2.
Найти неопределенный интеграл ![]() .
.
Решение.
Положим х + 1 = t,
тогда х = t
– 1; ![]() =
= ![]() ;
;
![]() =
= ![]() .
Продифференцировав
х + 1 = t, получим dх
=
dt.
=
.
Продифференцировав
х + 1 = t, получим dх
=
dt.
=
![]() =
= ![]() =
= ![]() - 2
- 2![]() +
+ ![]() =
- 2
=
- 2![]() +
+![]() =
=
![]() - 2
- 2 ![]() +
+ ![]() =
+
=
+ ![]() -
- ![]() + С =
+ С = ![]() +
+
![]() -
- ![]() + С.
+ С.
Метод интегрирования по частям. Пусть функция u = u(х) и v = v(х) определены и непрерывно дифференцируемые функции, то справедлива формула интегрирования по частям:
 =
uv
-
=
uv
-  .
.
Пример
3.
Найти
![]() .
.
Решение.
Обозначим
u
= ![]() ;
dv
= dх,
;
dv
= dх,
![]() =
= ![]() ,т.е. v
= х; du
= (
)'
dх.
По формуле (1) получаем:
,т.е. v
= х; du
= (
)'
dх.
По формуле (1) получаем:
![]() = х
–
= х
– ![]() = х
–
= х
– ![]() = х
- х + С = х (
= х
- х + С = х (![]() )+
С.
)+
С.
Таблица основных интегралов
|
|
|
|
|
|
|
|
|
|
|
|
Тема: «Вычисление определённых интегралов»
Теоретическая часть
Определенный
интеграл
– это общий предел всех интегральных
сумм функции f(х)
на отрезке [а,
b].
Определенный интеграл обозначается:
![]() ,
где f(х)
– подынтегральная функция; х – переменная
интегрирования; число а
называется
нижним
пределом
интеграла,
b
– верхним;
[а,
b]
– промежуток
интегрирования.
,
где f(х)
– подынтегральная функция; х – переменная
интегрирования; число а
называется
нижним
пределом
интеграла,
b
– верхним;
[а,
b]
– промежуток
интегрирования.
Если
F(х)
– первообразная функция для непрерывной
функции у = f(х),
т.е. F'(х)
= f(х),
то имеет место формула:
=
F(х)|![]() =
F(b)
– F(а).
Это формула Ньютона – Лейбница –
основная формула интегрального
исчисления, устанавливающая связь между
определенным и неопределенным интегралом.
=
F(b)
– F(а).
Это формула Ньютона – Лейбница –
основная формула интегрального
исчисления, устанавливающая связь между
определенным и неопределенным интегралом.
Определенный интеграл – это разность значений любой первообразной функции для f(х) при верхнем и нижнем пределах интегрирования. Разница между определенным и неопределенным интегралами: определенный интеграл – это число, а неопределенный интеграл – это функция.
Основные свойства определенного интеграла
При перестановке пределов изменяется знак интеграла:
= - ![]() .
.
Интеграл с одинаковыми пределами равен нулю:
![]() = 0.
= 0.
Отрезок интегрирования можно разбивать на части:
![]()
![]() .
.
Определенный интеграл от алгебраической суммы(разности) функций равен алгебраической сумме(разности) их определенных интегралов:
![]() =
=
![]()
![]() .
.
Постоянный множитель можно выносить за знак определенного интеграла:
![]() = С
.
= С
.
Если функция f(х)
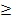 0
всегда на отрезке [а,b],
то
0
всегда на отрезке [а,b],
то

Если f(х)
 g(х)
всюду на
отрезке [а,b],
то
.
g(х)
всюду на
отрезке [а,b],
то
.
Пример
1.
Вычислите: ![]() .
.
Решение. Применим формулу Ньютона – Лейбница и свойства определенного интеграла:
= 3 ![]() =
|32
=
=
|32
= ![]() -
- ![]() = 27 – 8 = 19.
= 27 – 8 = 19.
Пример
2.
Вычислите: ![]() .
.
Решение.
Обозначим 4х + 3 = z,
откуда 4dх
= dz
или dх
= ![]() ;
при х = – 1, tн
=
– 4 + 3 = – 1; при х = 1, tв
=
4 +3 = 7. Следовательно,
;
при х = – 1, tн
=
– 4 + 3 = – 1; при х = 1, tв
=
4 +3 = 7. Следовательно,
![]() =
=![]() =
= ![]()
![]() =
=
![]() =
=
![]() .
.
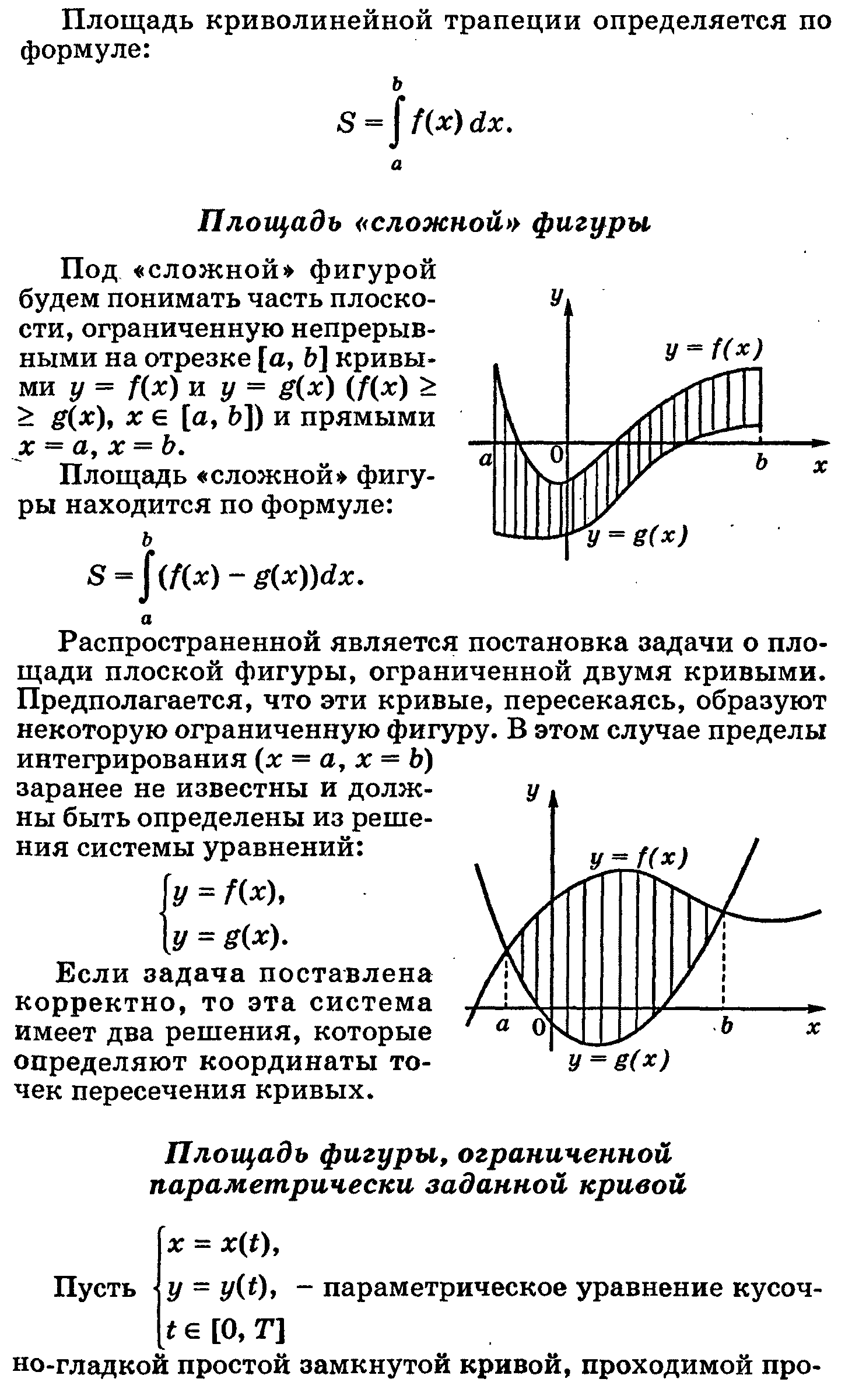
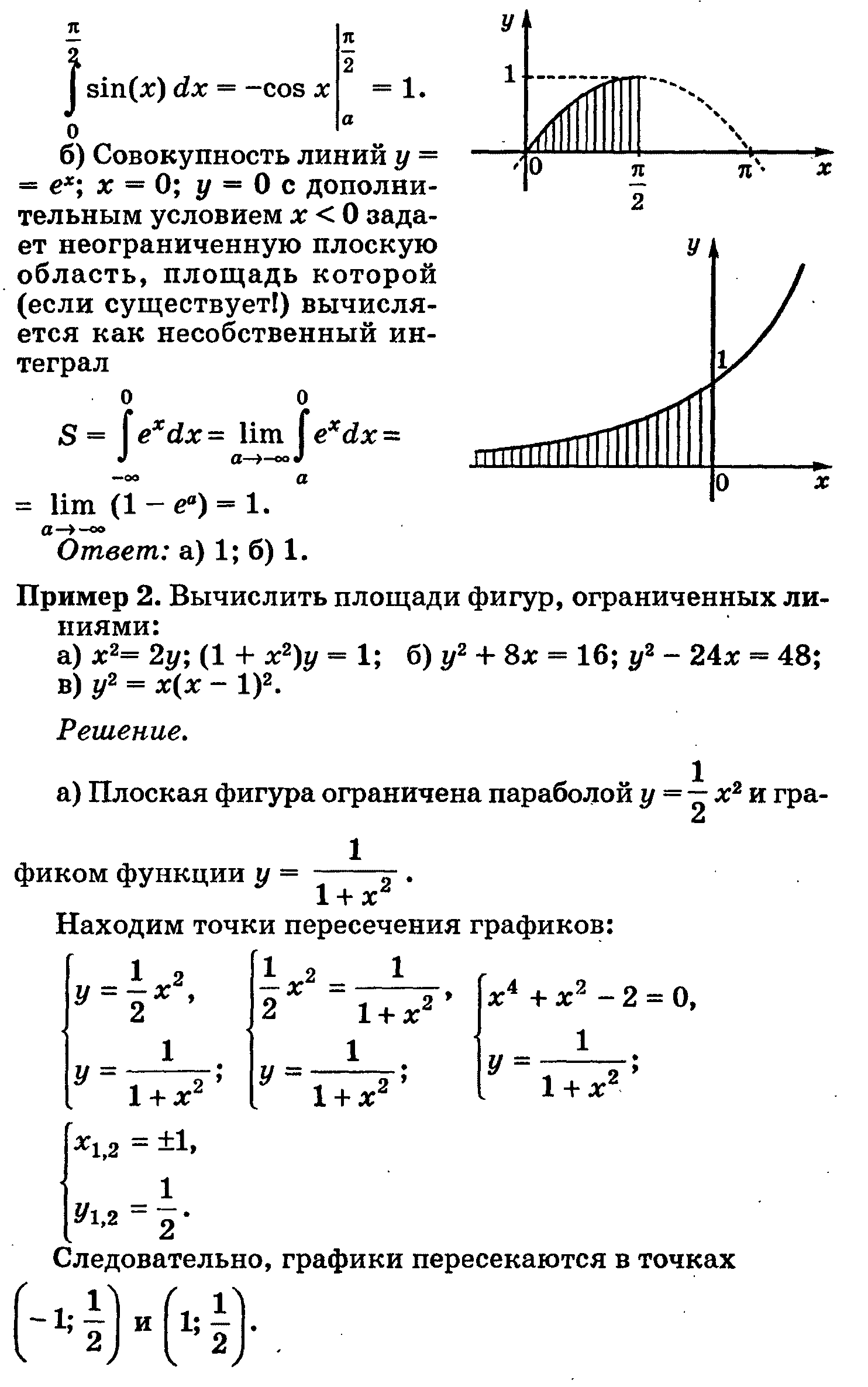
Тема: «Геометрические приложения определенного интеграла»
Теоретическая часть




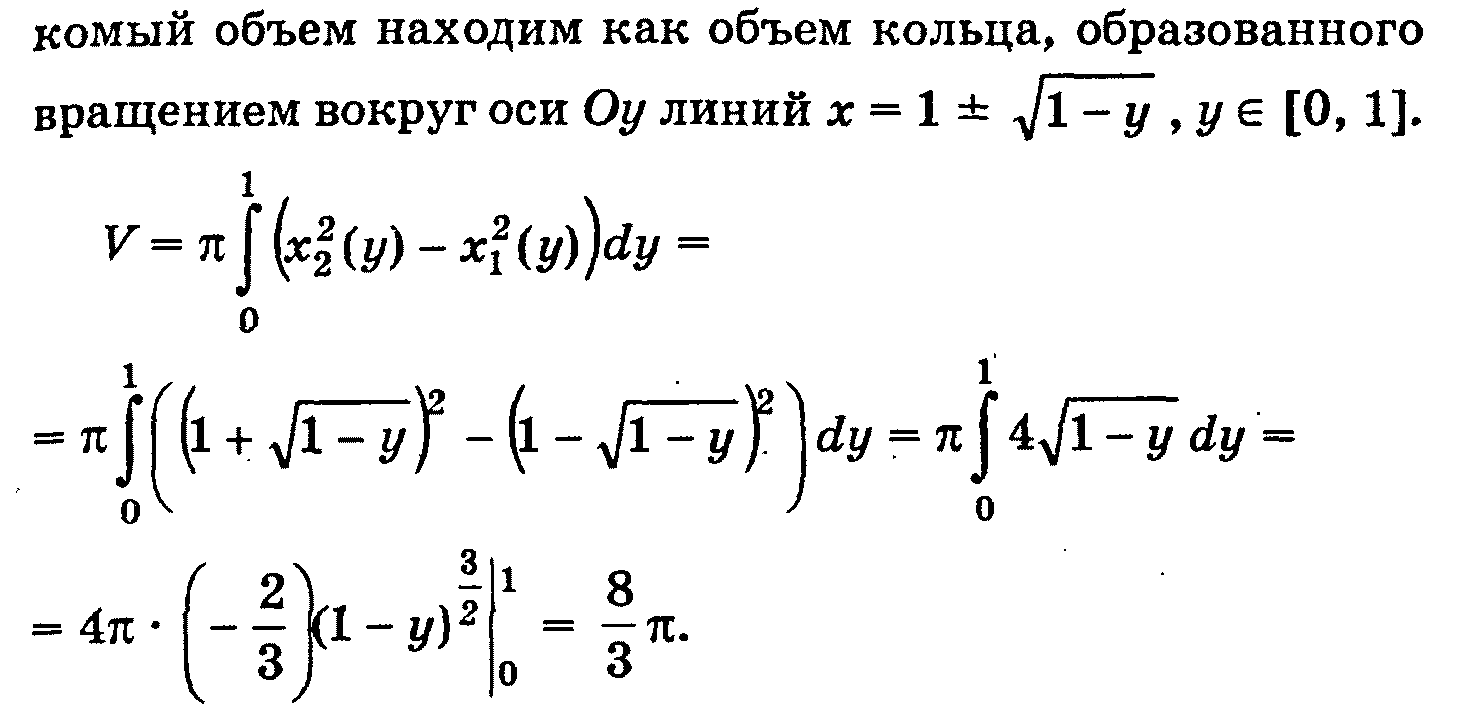
Тема: «Решение однородных обыкновенных дифференциальных уравнений первого порядка»
Теоретическая часть

Тема: «Действия над комплексными числами, заданными в алгебраическом виде»
Теоретическая часть

Пример 1: Найдите сумму комплексных чисел:
Пример 2: Найдите произведение комплексных чисел:
![]()
![]()
Произведение комплексных чисел в алгебраической форме:
![]()
Пример 3: Выполните действия
![]()

Частное комплексных чисел в алгебраической форме:
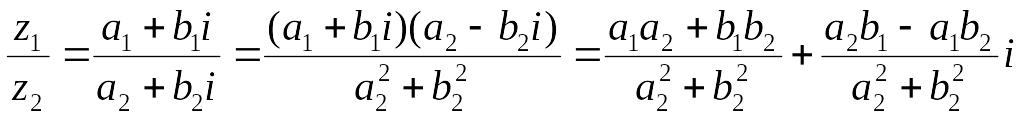
Пример 4: Выполните действие
![]()
![]()
П![]() ример
5: Найти модуль числа и число, противоположное
и сопряженное комплексному числу
ример
5: Найти модуль числа и число, противоположное
и сопряженное комплексному числу
Модуль числа
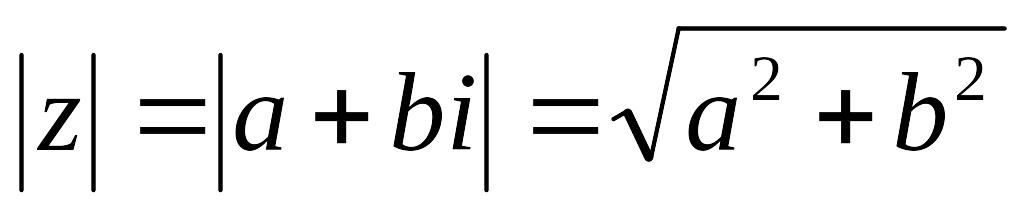 :
:
![]()
![]()
П
 ротивоположное
число
ротивоположное
число
Сопряженное число
Тема: «Умножение и деление комплексных чисел в тригонометрической форме»
Теоретическая часть
У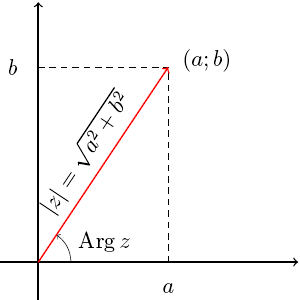 комплексных чисел есть удобное и
наглядное геометрическое представление:
число z = a + bi можно изображать
вектором с координатами (a; b) на
декартовой плоскости (или, что почти то
же самое, точкой — концом вектора
с этими координатами). При этом сумма
двух комплексных чисел изображается
как сумма соответствующих векторов
(которую можно найти по правилу
параллелограмма). По теореме Пифагора
длина вектора с координатами (a; b)
равна
комплексных чисел есть удобное и
наглядное геометрическое представление:
число z = a + bi можно изображать
вектором с координатами (a; b) на
декартовой плоскости (или, что почти то
же самое, точкой — концом вектора
с этими координатами). При этом сумма
двух комплексных чисел изображается
как сумма соответствующих векторов
(которую можно найти по правилу
параллелограмма). По теореме Пифагора
длина вектора с координатами (a; b)
равна
![]() .
Эта величина называется модулем
комплексного числа z = a + bi и
обозначается |z|. Угол, который этот
вектор образует с положительным
направлением оси абсцисс (отсчитанный
против часовой стрелки), называется
аргументом комплексного числа z и
обозначается Arg z. Аргумент определен
не однозначно, а лишь с точностью
до прибавления величины, кратной 2π
радиан (или 360°, если считать в градусах) —
ведь ясно, что поворот на такой угол
вокруг начала координат не изменит
вектор. Но если вектор длины r образует
угол φ с положительным направлением
оси абсцисс, то его координаты равны
(r · cos φ; r · sin φ).
.
Эта величина называется модулем
комплексного числа z = a + bi и
обозначается |z|. Угол, который этот
вектор образует с положительным
направлением оси абсцисс (отсчитанный
против часовой стрелки), называется
аргументом комплексного числа z и
обозначается Arg z. Аргумент определен
не однозначно, а лишь с точностью
до прибавления величины, кратной 2π
радиан (или 360°, если считать в градусах) —
ведь ясно, что поворот на такой угол
вокруг начала координат не изменит
вектор. Но если вектор длины r образует
угол φ с положительным направлением
оси абсцисс, то его координаты равны
(r · cos φ; r · sin φ).
Тригонометрическая
форма комплексного числа:
![]() ,
где
,
где
![]() ,
,
![]()
Пример
1: Записать
в тригонометрической форме комплексное
число
![]()
Решение:
Решение:
Найдем
![]() :
:
![]() ,
откуда
,
откуда
![]() ,
т.к. точка
,
т.к. точка
![]()
лежит в третьей четверти.
Учитывая
![]() ,
имеем:
,
имеем:
![]()
Произведение комплексных чисел:
![]()
Пример 2: Выполните действие
![]()
![]()
![]()
![]()
![]()
Частное комплексных чисел:
![]()
Пример 3: Выполните действие

![]()
![]()
![]()
![]()
![]()
Формула Муавра:
Пример 4: Выполните действие
![]()
![]()
![]()
Внимание!
Ни в коем случае нельзя использовать
четность косинуса, нечетность синуса
и проводить дальнейшее «упрощение»
записи:
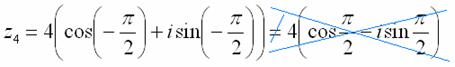
Рассмотрим
уравнение
![]() ,
или, то же самое:
,
или, то же самое:
![]() .
Здесь «эн» может принимать любое
натуральное значение, которое больше
единицы. В частности, при
.
Здесь «эн» может принимать любое
натуральное значение, которое больше
единицы. В частности, при
![]() получается
квадратный корень
получается
квадратный корень
![]()
Уравнение
вида
имеет
ровно
![]() корней
корней
![]() ,
которые можно найти по формуле:
,
которые можно найти по формуле:
![]() ,
где
,
где
![]() –
это модуль комплексного числа
–
это модуль комплексного числа
![]() ,
,
![]() –
его аргумент, а параметр
–
его аргумент, а параметр
![]() принимает
значения:
принимает
значения:
![]()
Тема: «Вычисление вероятности событий с элементами комбинаторики»
