Задание 5.

Игнорированием ориентации дуг перейти от ориентированного графа G к неориентированному графу G´. Изобразить полученный граф G´ графически.

Замечание. Можно рассматривать графы без учета ориентации их дуг. В этом случае граф принято называть неориентированным графом. На рисунке дуги такого графа изображаются без стрелок и называются неориентированными дугами или ребрами. Заметим, что если граф неориентированный, то его множество дуг будет состоять уже не из двоек, а из двухэлементных подмножеств множества X_G вида: P_G = {{a, b}: a, b ϵ X_G }.

Решение:

G´

X_G´ = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

P_G´ = {{1,2},{1,3},{1,8},{2,4},{2,6},{2,9},{2,9},{3,4},{3,5},{3,8},{4,6}, {4,10},{5,5},{5,7},{5,9},{6,10},{7,8},{8,9},{8,10},{10,10}}

Задание 6.

Сформировать матрицы инцидентности и смежности неориентированного графа G´.

Определение. Пусть задан граф G´=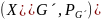 - неориентированный. Матрицей смежности графа G´ называется матрица A(G´) размерности [n x n], где n – мощность множество вершин, с элементами a_ij´, которые определяются следующим условием:

a_ij´ =

Замечание. Отметим, что по определению матрица смежности неориентированного графа всегда будет симметричной матрицей.

Определение. Пусть граф G´ некоторый неориентированный граф. Матрицей инцидентности графа G´ называется B(G´) размерности [n x m], где n – мощность множества вершин, m – мощность множества дуг, с элементами b_ij , которые определяются следующим условием:

b_ij =

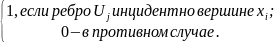
Замечание. Отметим важный факт, что матрица инцидентности графа G´ содержит в себе информацию о нумерации (именах) ребер графа.

Решение:

A(G´) =

	1	2	3	4	5	6	7	8	9	100
1	0	1	0	0	0	0	0	0	0	0
2	0	0	0	0	0	1	0	0	1	0
3	1	0	0	1	0	0	0	1	0	0
4	0	1	0	0	0	0	0	0	0	1
5	0	0	1	0	1	0	1	0	0	0
6	0	0	0	1	0	0	0	0	0	0
7	0	0	0	0	0	0	0	1	0	0
8	1	0	0	0	0	0	0	0	1	0
9	0	0	0	0	1	0	0	0	0	0
10	0	0	0	0	0	1	0	1	0	1

G´

B(G´) =

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
1	0	0	1	0	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0
2	1	1	1	1	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0
3	0	0	0	0	0	0	0	0	0	1	0	0	1	0	0	1	1	0	0
4	0	1	0	0	0	0	0	0	0	0	0	0	0	1	1	0	1	0	0
5	0	0	0	0	0	0	0	1	0	0	1	0	0	0	0	1	0	1	0
6	1	0	0	0	1	0	0	0	0	0	0	0	0	0	1	0	0	0	0
7	0	0	0	0	0	0	0	0	1	0	1	0	0	0	0	0	0	0	0
8	0	0	0	0	0	1	1	0	1	1	0	1	0	0	0	0	0	0	0
9	0	0	0	1	0	0	1	1	0	0	0	0	0	0	0	0	0	0	0
10	0	0	0	0	1	1	0	0	0	0	0	0	0	1	0	0	0	0	1