Задание 1.

Преобразовать исходную матрицу в матрицу длин, включая соответствующие символы.

Определение. Пусть граф G=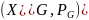 – нагруженный ориентированный граф. Матрицей длин графа G называется матрица S(G)_{[n x n]} с элементами s_ij, которые определяются следующим образом:

s_ij=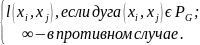

Решение:

Исходная матрица

	1	2	3	4	5	6	7	8	9	100
1	0	3	0	0	0	0	0	0	0	0
2	0	0	0	0	0	21	0	0	15	0
3	13	0	0	5	0	0	0	13	0	0
4	0	16	0	0	0	0	0	0	0	2
5	0	0	7	0	4	0	8	0	0	0
6	0	0	0	6	0	0	0	0	0	0
7	0	0	0	0	8	0	0	9	0	0
8	12	0	7	0	0	0	7	0	9	0
9	0	17	0	0	5	0	0	0	0	0
10	0	0	0	0	0	18	0	19	0	13

Матрица длин

	1	2	3	4	5	6	7	8	9	10
1	∞	3	∞	∞	∞	∞	∞	∞	∞	∞
2	∞	∞	∞	∞	∞	21	∞	∞	15	∞
3	13	∞	∞	5	∞	∞	∞	13	∞	∞
4	∞	16	∞	∞	∞	∞	∞	∞	∞	2
5	∞	∞	7	∞	4	∞	8	∞	∞	∞
6	∞	∞	∞	6	∞	∞	∞	∞	∞	∞
7	∞	∞	∞	∞	8	∞	∞	9	∞	∞
8	12	∞	7	∞	∞	∞	7	∞	9	∞
9	∞	17	∞	∞	5	∞	∞	∞	∞	∞
10	∞	∞	∞	∞	∞	18	∞	19	∞	13

S(G) =