КОНСПЕКТ ЛЕКЦИЙ

по дисциплине «Моделирование в менеджменте»

составитель доц. каф. МВС Загорудько В.Л. (80 стр)

СОДЕРЖАНИЕ

Лекция 1 2

Основные понятия теории моделирования систем 2

Лекция 2 15

Классификация видов моделирования систем 15

Лекция 3 21

Методология структурного анализа и проектирования 21

Лекция 4. 29

Сети Петри 29

Лекция 5. 38

Детерминированные конечные автоматы 38

Лекция 6. 47

Вероятностные модели систем 47

Лекция 7 53

Этапы машинного моделирования систем 53

Лекция 8 64

Этапы машинного моделирования систем 64

Лекция 1 Основные понятия теории моделирования систем Методологическая основа моделирования

Моделирование – это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала с помощью объекта-модели путем проведения эксперимента с моделью.

Объект (лат. objectum – предмет) – все то, на что направлена человеческая деятельность. Технический объект – машина, механизм, технический комплекс, технологический процесс, а также любой их компонент, выделяемый в процессе моделирования путем деления структуры целостного объекта на отдельные блоки, части, элементы.

Гипотеза – определенные предсказания, предположения, основанные на небольшом количестве опытных данных, наблюдений, догадок. Быстрая и полная проверка выдвигаемых гипотез может быть проведена в ходе специально поставленного эксперимента. При формулировании и проверке правильности гипотез большое значение в качестве метода суждения имеет аналогия.

Аналогия – суждение о каком-либо частном сходстве двух объектов.

Эксперимент – процедура организации наблюдений каких-то явлений, которые осуществляют в условиях, близких к естественным, либо имитируют их. Различают пассивный эксперимент, когда исследователь наблюдает протекающий процесс, и активный, когда наблюдатель вмешивается и организует протекание процесса.

В общем процесс моделирования представлен следующим образом: используя априорные (ранее известные) данные об объекте, выдвигается гипотеза, по которой на основе аналогии строится наглядная упрощенная логическая схема (модель) и с ней проводится эксперимент для изучения свойств объекта.

Модель (лат. modulus – мера) – объект-заместитель объекта-оригинала, обеспечивающий изучение некоторых свойств оригинала.

Пример 1. Рассмотрим физическую систему: тело массой m скатывающееся по наклонной плоскости с ускорением a, на которое воздействует сила F. Исследуя такие системы, Ньютон получил математическое соотношение: F=ma. Это физико-математическая модель системы или математическая модель физической системы. При описании этой системы (построении этой модели) приняты следующие гипотезы: 1) поверхность идеальна (т.е. коэффициент трения равен нулю); 2) тело находится в вакууме (т.е. сопротивление воздуха равно нулю); 3) масса тела неизменна; 4) тело движется с одинаковым постоянным ускорением в любой точке.

Пример 2. Совокупность предприятий функционирует на рынке, обмениваясь товарами, сырьем, услугами, информацией. Если описать экономические законы, правила их взаимодействия на рынке с помощью математических соотношений, например, системы алгебраических уравнений, где неизвестными будут величины прибыли, получаемые от взаимодействия предприятий, а коэффициентами уравнения будут значения интенсивностей таких взаимодействий, то получим математическую модель экономической системы, т.е. экономико-математическую модель системы предприятий на рынке.

При этом если результаты моделирования по каким-либо причинам не удовлетворяют исследователя, то процесс моделирования начинается с возврата на предыдущие стадии, то есть моделирование – процесс итерационный (рис. 1).

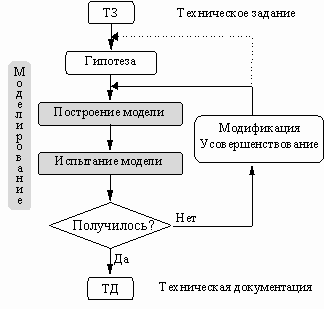
Рис. 1. Итерационный характер процесса моделирования

Моделирование базируется на математической теории подобия, согласно которой абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании большинства систем (за исключением, возможно, моделирования одних математических структур другими) абсолютное подобие невозможно, и основная цель моделирования - модель достаточно хорошо должна отображать функционирование моделируемой системы.