3.6.3 Определение постоянной составляющей приведенного момента инерции и момента инерции маховика. .

В основу расчета положен метод Н.И. Мерцалова. Для определения изменения кинетической энергии машины предварительно определяем работу движущих сил . Для i-гo положения:

где

Тогда

Изменение кинетической энергии звеньев с постоянным при­веденным моментом инерции равно :

,

где - кинетическая энергия звеньев, создающих переменную составля­ющую . По методу Мерцалова, определяется приближенно по сред­ней угловой скорости :

Далее из полученного за цикл массива значений , находим максимальную и величины используя которые, вычисляем максимальный перепад кинетической энергии:

Тогда необходимая величина , при которой имеет место вра­щение звена приведения с заданным коэффициентом неравномерности , равна:

Момент инерции маховика определяется как

приведенный момент инерции всех вращающихся масс машины (рото­ра, зубчатых колес, кривошипа). задано в условии курсового проекта.

Иногда величина может оказаться больше полученного значения . Это означает, что не требуется установки маховика .

3.6.4 Определение закона движения звена приведения.

С помощью зависимости 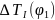, используемой при определении постоянной составляющей приведенного момента инерции по методу Мерцалова , можно получить зависимость угловой скорости звена приве­дения

Для любого положения кинетическая энергия звеньев, обладающих постоянным приведенным моментом инерции , равна :

где

Угловое ускорение определяется из дифференциального уравне­ния движения звена приведения:

3.6.5 Схема алгоритма программы. Исследование динамической нагруженности машинного агрегата.

Рассмотренные в предыдущих параграфах материалы позволяют разработать программу исследования динамической нагруженности машинного агрегата. В качестве объекта исследования взята технологическая ма­шина, в которой основным исполнительным механизмом является кривошипно-ползунный механизм.

Осуществляется ввод данных (блок 1). Пример подготовки исход­ных данных показан в таблице. Следует обратить внимание на соответствие направления вращения кривошипа , знака F, по отношению к положительному направлению соответствующей оси координат, а также на знак величины эксцентриситета е.

В блоке 2 вычисляются угловой шаг 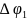, , максимальная коорди­ната ползуна, и присваивается начальное значение обобщенной координате.

Далее в цикле по (блоки 4-9) вычисляются кинематические характеристики рычажного механизма, динамические характеристики

кинетическая энергия , работа сил сопротивления

По окончании цикла определяется приведенный момент движущих сил ( блок 10 ).

В новом цикле (блоки 11-12) производится вычисление , ,

В подпрограмме (блок 13 ) из массива , находятся экстремаль­ные значения , что позволяет в блоке 14 определить величины , , а также 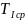, и .

После вычисления в цикле (блоки15 и16) T, , производится печать результатов расчета (блок 17).

Начало

Исходные данные

, ( )

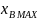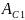= 0

i=1,n

Кинематические

характеристики

, , ,

i>1

i>1

нет

да

да

A

A

A

A

i=1,n

Поиск

максимального и

минимального

элементов

i=1,n

Печать результатов

Конец