3.6. Динамическая модель машинного агрегата.

В движении входного звена исполнительного рычажного механизма имеют место колебания угловой скорости, основными причинами которых являются:

1) несовпадение законов изменения сил сопротивления и движущих сил

в каждый момент времени ; 2 ) непостоянство приведенного момента инерции звеньев исполнитель­ного и некоторых вспомогательных механизмов.

Двигатель		Передаточный механизм				Основной (испол­нительный) рычаж­ный механизм
			Вспомогательные (кулачковые, рычажные и др.) механизмы

Чтобы учесть влияние названных причин на закон движения входного звена исполнительного механизма, составляется упрощенная динамическая модель машинного агрегата и на ее основе – математическая модель, устанавливающая функциональную взаимосвязь исследуемых параметров.

Наиболее простой динамической моделью машинного агрегата может быть одномассовая модель представленная ниже:

В качестве такой модели рассматривается условное вращающее звено- звено привидения, которое имеет момент инерции относительно оси вращения (приведенный момент инерции) и находится под действием момента сил (приведенного момента сил). В свою очередь

где

- приведенный момент сил сопротивления;

Динамические характеристики и должны быть такими, чтобы закон вращения звена привидения был таким же, как и у главного вала машины (кривошипа 1 основного исполнительного рычажного механизма), т.е. .

3.6.1 Определение приведенных моментов сил сопротивления и движущих сил.

Определение выполняется из условия равенства мгновенных мощностей:

· =

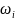Откуда = ·sign( ), где

проекции силы на оси координат;

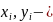проекции аналогов скорости точки приложения силы ;

передаточная функция от i-го звена, к которому приложен момент , к звену 1

sign( )= -1 при направлении вращении звена 1 по часовой стрелке .

Для вертикального механизма получаем:

= ·sign( )=

Сила 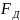в изображенном случае отрицательна. Во втором положении:

= =1608,33м

Приведенный момент определяется из условия, что при установившемся режиме движения изменение кинетической энергии машины за цикл =0, т.е.

T= , и за цикл

Работа движущих сил вычисляется по формуле:

Интегрирование выполняется численным методом по правилу трапеций

·

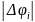
где 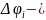шаг интегрирования в радианах

С учетом при

3.6.2 Определение переменной составляющей приведенного момента инерции и его производной .

Переменная составляющая определяется из условия равенства кинетических энергий, т.е. кинетическая энергия звена привидения, имеющего момент инерции , равна сумме кинетических энергий звеньев, характеризуемых переменными передаточными функциями :

Разделив это выражение на , с учетом того , что ,

получим :

= 0,089кг·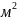

Производная необходимая в последующем для определения закона движения звена приведения, имеет вид :

sign( =0,002 кг·