3.2 Геометрический синтез рычажного механизма.
Входные параметры для выполнения геометрического синтеза:
S – ход поршня;
– максимальный
угол давления.
= 0,065 (м).
0,181 (м).
=0,35·lAB=
0,35∙0,181=0,630 (м).
Масса шатуна
AB:
(кг).
Масса поршня: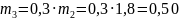
(кг).
Масса кривошипа:
=3,6
(кг).
Моменты инерции относительно центров масс:
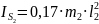= 0,17·1,8·
=
0,010 (
)
= 0,33·3,6·
=
0,0051
)
3.3 Построение плана положений механизма.
начальная обобщенная
координата соответствующая наиболее
удаленному крайнему положению ползуна:
=
=90⁰
Выбор масштабного
коэффициента
:
для этого принимаем ОА=47 мм.
=
=
=0,001
(м/мм);
OA=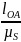
=
=60
(мм);
AB=
=
=240
(мм);
A
=
=
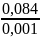=84
(мм).
3.4 Определение кинематических характеристик кривошипно-ползунного механизма и контрольный расчет их для положения №2 (аналитически).
Кинематические характеристики определяются по формулам, выведенным для метода замкнутого векторного контура.
Расчет кинематических характеристик:
=0,06·0,5=0,03
(м);
=0,06·0,866=0,052
(м);
=0,06+
=(
)/
0,03)/0,240=
0,125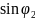
=(
)/
(0,298 – 0,052)/0,240=0.99;
=
-0,22
+
=0,06·0,5+0,240·(
)=0,037(м).
+
=
=
=
=
=
−0,0595(м);
=0,03
+0,084·(−0,125) = 0,0195 (м);
=0,052
+0,084·0,99 =0,135 (м);
=
-0,06∙0,866 - (-0,22) ·0,084·0,99= -0,034 (м);
= 0,06·0,5+(−0,22)·0,084·(−0,125) = 0,048 (м);
−
=
=−0,06·0,5-(-
·0,084 0,99 - 0,084·
(-0,125) = − 0,035(м);
−
=
=−0,047·0,866+(-0,076)
·0,117
·(-0,133)
-
0,117
·
·0,99
= -0,289
(м);
=
=
;
=0,03−0,298=0,002
(м);
Для сравнения
произведем определение кинематических
характеристик построением плана аналогов
скоростей. Для построения плана аналогов
скоростей примем
=
.
В этом случае отрезок Pa
изображает аналог скорости точки А:
Pа=ОА.
Известно, что Pа
ОА.
Поскольку между скоростями и аналогами
скоростей существует пропорциональность,
то для точки В записываются аналогичные
векторные уравнения:
Построение точки на плане находим по теореме подобия. Произведем графические расчеты
=
=pb
=36·0,001=0,036
(м);
=ab
ab
0,217;
=p
=0,046
(м);
Сопоставление
расчетов
:
|
|
|
Аналитический |
-0,220 |
0,037 |
Графический |
-0,217 |
0,036 |
3.5. Обработка индикаторной диаграммы и определение внешних сил, действующих на поршень.
Индикаторная диаграмма представляет собой графическое изображение зависимости давления P от перемещения ползуна S. Требуется определить значение давления Р и силы А для всех положений механизма.
Для обработки индикаторной диаграммы выбираем масштабный коэффициент:
=
=3.8·
0.035
.
Сила, действующая на поршень, рассчитывается по формуле:
=
,
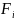где
- площадь днища поршня:
=π·
/4,
где d
– диаметр поршня;
d=84 (мм)
5539
(
Результаты расчетов сводим в таблицу.
№ |
|
, Н |
1 |
177 |
-49397 |
2 |
152 |
-42920 |
3 |
110 |
-30978 |
4 |
67 |
-18698 |
5 |
26 |
-7256 |
6 |
7 |
-1953 |
7 |
0 |
0 |
8 |
2 |
-558 |
9 |
8 |
-2232 |
10 |
21 |
-5880 |
11 |
44 |
-12558 |
12 |
75 |
-20652 |
13 |
89 |
-24559 |
,
мм