Сравнение и однородность Задача 6
В пожарную часть поступили новые мобильные средства пожаротушения оснащенные насосными установками нового поколения.
Требуется определить (сравнить) время подготовки насосной установки нового МСП и насосной установки эксплуатируемого МСП для забора воды из водопровода и пуска её в магистральные рукавные линии.
Для этой цели были проведены две серии в 20 и 30 равноточных измерений действий одних и тех же водителей, примерно одинаковой профессиональной подготовленности и психологической устойчивости по подготовке насосных установок и запуску их в работу.
Получили средние значения времени - 1 = 24,56 с., 2 = 23,80 с. и дисперсии - = 1,28, = 1,59.
Требуется сравнить средние значения измеряемых величин и решить вопрос об их значимости или расхождении с надежность p = 0,95.
Итак: n1 = 20; 1 = 24,56 с., = 1,28
n2 = 30; 2 = 23,8 с., = 1,59
Сначала сравним дисперсии:
Fpac
=
=
=
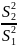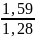1,24 - критерий
Фишера расчётный
=
20-1 =19 (степени
свободы)
= 30-1 = 29
Fpac =1,24 < Fтабл =2.57; Т.о. дисперсии однородны.
=
=
=
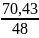= 1,47
(средняя дисперсия)
=
=
=
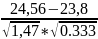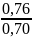≈ 1,1;
=
= 48 (степени
свободы)
≈ 1,1 < ≈ 2,01; Т.о. время однородно , т. е.
обе совокупрости принадлежат одной генеральной совокупности и имеют одно общее математическое ожидание.
сравнение и однородность Задача 7
В гарнизоне пожарной охраны были проведены эксперименты по определению параметров оперативно-тактических действий по развертыванию насосно-рукавных систем для транспортирования и подачи огнетушащих веществ. Измеряемые величины представлены в таблице:
Требуется:
определить доверительный интервал в выборке X;
сравнить дисперсии и средние выборок X и Y.
Все расчеты можно призвести с помощью табл. Exel. Вот формулы:
По выборке X - кол-во измерений nx = 14
найдём
среднюю
=
= 20,571
потом
– дисперсию
по X
=
=
=
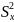19,1
и
среднеквадратическое
=
=
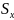= 4,54
Тогда доверительный интервал:
∆
=
=
= 2.38
;
где =1,96 – коэффициент Стьюдента, с доверительной вероятностью 0,95;
По выборке Y - кол-во измерений ny = 14
найдём
среднюю
=
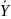= 21,64
потом
– дисперсию
по Y
=
=
=
12,66
Cравним дисперсии и средние выборок X и Y.
Сначала сравним дисперсии:
Fpac
=
=
=
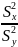1,51 - критерий
Фишера расчётный
=
=
14-1 = 13 (степени
свободы)
Fpac =1,24 < Fтабл =2.59; Т.о. дисперсии однородны.
=
=
=
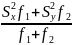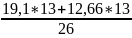= 15,88
(средняя дисперсия)
=
=
=
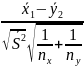= 0.245;
=
= 26 (степени
свободы)
= 1,12 < = 2,59; Т.о. время однородно , т. е.
обе совокупрости принадлежат одной генеральной совокупности и имеют одно, общее математическое ожидание.
Метод наименьших квадратов (2 задачи)