
- •II.Для проверки на адекватность необходимо
- •Проверяем дисперсии и на однородность:
- •Сравнение и однородность Задача 6
- •Задача 1
- •Составим матрицу пфп 2к :
- •Составим матрицу пфп 22 :
- •Доверительный интервал Задача 2
- •Требуемое количество измерений, Задача 3 доверительный интервал
- •Определить коэффициент корреляции (2 задачи)
- •Вариационный ряд (3 задачи)
- •Вариационный ряд Задача 2
- •Вариационный ряд Задача 3
- •3) Вычисляем накопленные относительные частоты :
- •IV. Составляем эмпирическую функцию распределения , которая
Параметры фактора и интервалы между ними
Определить количество значений параметров фактора и интервала между их значениями. В эксперименте используются пожарное оборудование массой от 2 до 28 кг.
Количество значений фактора (q) определяется по формуле :
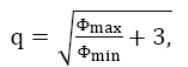 и
должно быть не меньше трёх
и
должно быть не меньше трёх
Интервалы между факторами определяются по формуле:
![]() где
где
Фmax и Фmin - max и min значения фактора.
Т.о.
количество значений фактора q
=
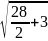 = 4.1;
= 4.1;
интервал
между факторами
H
=
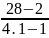 = 8.4;
= 8.4;
Задачи на графо - аналитический метод (3 задачи)
Задача 1
Используя графо - аналитический метод вывести уравнение регрессии для определения времени по перемещению пожарного оборудования вручную. Затраты времени зависят от массы перемещаемого пожарного оборудования – m и расстояния перемещения – L. Масса перемещаемого пожарного оборудования и инструмента изменяется в пределах от 3 до 21 кг, а расстояние перемещения от 0,9 до 11 м.
Временные параметры представлены в таблице 1 и 2.
Таблица 1.
Зависимость затрат времени (τ) от массы перемещаемого пожарного оборудования при постоянном расстоянии (L - const), равном 4,6 м.
Таблица 2.
Зависимость затрат времени (τ) от расстояния перемещаемого пожарного оборудования при постоянной массе (m - const), равной 11 кг.
В этой задаче я сразу время , заданное в минутах, перевёл в сек. (в табл. красным) .Так нагляднее.
Ур-ние регресии для массы: 𝛕1 = a1 m+b01 , тогда (найдём всевозможные средние):
mср= = 10,67кг;
= 10,67кг;
 =
=
 = 5.33;
= 5.33;
 =
= = 16;
= 16;
 =
=
 = 15.4 сек;
= 15.4 сек;
 =
=
 = 13,2;
= 13,2;
 =
=
 = 17,6;
= 17,6;
коэффициенты уравнения 1:
a1
=
 =
=
 =
=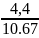 = 0.41; b01=𝛕ср1
-
a1*
mср=15,4
- 0,41*10,67=11.02;
= 0.41; b01=𝛕ср1
-
a1*
mср=15,4
- 0,41*10,67=11.02;
Ур-ние регресии для расстояния: 𝛕2 = a2 m+b02 , найдём все средние:
Lср
=
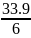 = 5.65;
= 5.65;
 =
= = 2.77;
= 2.77;
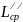 =
= = 8.53;
= 8.53;
 =
= = 20,1 сек;
= 20,1 сек;
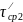 =
=
 = 9,062;
= 9,062;
 =
=
 =25,0;
=25,0;
коэффициенты уравнения 2:
a2
=
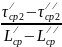 =
=
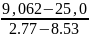 =
=
 = 2,76; b02=𝛕ср2
-
a1*
Lср=20,1
– 2,76*5.65=15,6;
= 2,76; b02=𝛕ср2
-
a1*
Lср=20,1
– 2,76*5.65=15,6;
вид ур-ния регрессии для двух факторов : 𝛕 = a1 m+a2 L+b0 находим b0 :
b0
= =
=
 =
=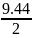 = 4.72;
= 4.72;
Таким образом получилось следующее ур-ние регрессии :
𝛕 = 0,41m+2,76 L+4,72
графо - аналитический метод Задача 2
Для решения вопросов оптимизации оперативно-тактических действий на горизонтальном участке местности, покрытом снежным покровом различной высоты hсн, были проведены эксперименты, результаты которых представлены в таблице:
hсн, см |
0 |
31 |
40 |
52 |
60 |
73 |
82 |
τ, сек |
66 |
104 |
136 |
180 |
210,5 |
270 |
305 |
Используя графо-аналитический метод:
-построить уравнение регрессии;
-проверить адекватность полученного уравнения по F-критерию; (проверить на адекватность - не хватает данных. Как определить дисперсию ошибки эксперимента? Нужны дополнительные опыты).
построить график τ = f (hсн).
I. Ур-ние регресии : 𝛕 = a1 h+b01 , тогда (найдём всевозможные средние):
hср=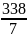 = 48,3см;
= 48,3см;
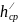 =
=
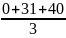 = 23.7;
= 23.7;
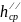 =
= = 66.8;
= 66.8;
=
 = 181,6 сек;
=
= 181,6 сек;
=
 =121.5;
=
=121.5;
=
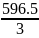 =198.8;
=198.8;
коэффициенты уравнения 1:
a1
=
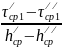 =
=
 =
=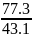 = 1.79 ≈
1,8;
= 1.79 ≈
1,8;
b01=𝛕ср1 - a1* hср=181.6 – 1.79*48.3 = 95.14 ≈ 95;
Т. о. уравнение регрессии : 𝛕 = 1,8 h+95 ;
Зная уравнение, теперь можно определить рассчётное время для каждого (любого) h
путём подстановки этого h в уравнение регрессии.
Например:
берём h=60,
тогда
 =
1,8*60+95=203,0 Теперь можно сравнить расчётное
время (
=
203,0) и измеренное время (при h=60
𝛕
=210,5 ). И сделтать вывод об адекватности
уравнения регрессии
.
=
1,8*60+95=203,0 Теперь можно сравнить расчётное
время (
=
203,0) и измеренное время (при h=60
𝛕
=210,5 ). И сделтать вывод об адекватности
уравнения регрессии
.
𝛕- = 210,5-203,0=6,5; - это есть отклонение расчётного времени при h = 60
II.Для проверки на адекватность необходимо
- Определить дисперсию отклонения расчётного времени по формуле:
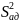 =
=
 =
=
 =
=
 ≈ 1650– дисперсия
отклонений
≈ 1650– дисперсия
отклонений
где N = 7 – количетво опытов, а P = 1 - количетво факторов
-
Определить
дисперсию ошибки
измерения
по формуле:
 (y)
=
(y)
=
 , где
, где
 =
= ;
- дисперсия ошибки измерений по каждому
опыту,
;
- дисперсия ошибки измерений по каждому
опыту,
где n -количество измерений.
В нашем задании (т.к. n = 1) дисперсию ошибки измерения определить невозможно (на ноль делить нельзя).
графо - аналитический метод Задача 3 (не указаны L=const=? и m= const=? )
Вывести уравнение регрессии для определения времени на перемещение пожарного оборудования вручную с помощью графо-аналитического метода. Затраты времени зависят от массы пожарного оборудования m, которая изменяется от 4 до 22 килограмм и от расстояния перемещения L, которое изменяется от 1,2 до 13 метров. Результата хронометражных наблюдений приведены в таблицах 1 и 2.
Таблица 1
Зависимость затрат рабочего времени (t) от массы перемещаемого пожарного оборудования (m) при постоянной длине (L=const)
Таблица 2
Зависимость затрат рабочего времени (t) от длины перемещения (L) при постоянной массе (m= const)
В этой задаче я сразу время , заданное в минутах, перевёл в сек. (в табл. красным) .Так нагляднее.
Ур-ние регресии для массы: 𝛕1 = a1 m+b01 , тогда (найдём всевозможные средние):
mср= = 11,0кг;
=
= 11,0кг;
=
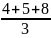 = 5,7;
=
= 5,7;
= = 16,3;
= 16,3;
=
 = 17,1 сек;
=
= 13,2;
=
= 17,1 сек;
=
= 13,2;
=
 = 21;
= 21;
коэффициенты уравнения 1:
a1
=
=
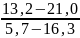 =
= = 0,74; b01=𝛕ср1
-
a1*
mср=17,1
- 0,74*11,0
≈
9,0;
= 0,74; b01=𝛕ср1
-
a1*
mср=17,1
- 0,74*11,0
≈
9,0;
Ур-ние регресии для расстояния: 𝛕2 = a2 L+b02 , найдём все средние:
Lср
=
 = 6.0;
=
= 6.0;
=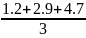 = 2.93;
=
= 2.93;
=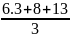 = 9.1;
= 9.1;
= = 25.9 сек;
=
= 25.9 сек;
=
 = 15.4;
=
= 15.4;
=
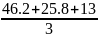 =28.3;
=28.3;
коэффициенты уравнения 2:
a2
=
=
 =
=
 = 2,1; b02=𝛕ср2
-
a1*
Lср=25,9
– 2,1*6,0 =
13,3;
= 2,1; b02=𝛕ср2
-
a1*
Lср=25,9
– 2,1*6,0 =
13,3;
вид ур-ния регрессии для двух факторов : 𝛕 = a1 m+a2 L+b0 находим b0 :
возьмём L=const=1,2 и m= const=4, тогда
b0
=
=
 =
= = 8,41;
= 8,41;
Таким образом получилось следующее ур-ние регрессии :
𝛕 = 0,74m+2,1 L+8,41
Задачи на сравнение и однородность ( 7 задач)
Задача 1
При проведении эксперимента по определению времени соединения водосборника с напорным патрубком насоса МСП были получены значения времени двумя исполнителями, которые представлены таблице:
Требуется проверить:
однородность статистической совокупности времени выполнения элемента ОТД по F-критерию;(взять среднеквадратическую S разделить на среднюю
 получим коэфф-нт вариации(V=
получим коэфф-нт вариации(V= .
Если V=
.
Если V= < 0.33, то
статистическая совокупность однородна);
< 0.33, то
статистическая совокупность однородна);однородность времени выполнения элемента ОТД первым и вторым исполнителями. (взять 2 дисперсии, разделить друг на дружку и сравнить с таблицей Фишера);(f1 = f2 =( n-1) = 16. Если дисперсии однородны , проверяем на однородность время выполнения)
Итак:
1)
Проверим на однородность всю статистическую
совокупность (все 34
значения
 )
)
=
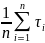 =
=
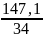 = 4.32;
= 4.32;
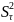 =
=
 =
=
 = 0,367; S=
= 0,367; S=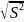 =0.6;
=0.6;
Тогда
коэффициент вариации : V=
=
 *100% ≈ 13.8% <
33%, где
*100% ≈ 13.8% <
33%, где
S - среднеквадратическая
вывод: вся статистическая совокупность времени однородна.
2) Проверим на однородность время первого и второго исполнителя.
по формулам: = ; = ;
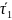 =4.388
;
=4.388
;
 =0.356
;
=0.356
;
 =4.265
;
=4.265
;
 =
0.371;
=
0.371;
Fpac
= =
=
 =
1,1 - критерий
Фишера расчётный
=
1,1 - критерий
Фишера расчётный
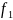 =
=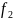 =
17-1 =16 (степени
свободы)
=
17-1 =16 (степени
свободы)
Fpac =1,1 < Fтабл =2.31; Т.о. дисперсии однородны.
 =
=
 =
=
 =
=
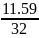 = 0.362
(средняя
дисперсия)
= 0.362
(средняя
дисперсия)
 =
=
 =
=
 = 0.53;
= 0.53;
 =
= =
32 (степени
свободы)
=
32 (степени
свободы)
=
0.53
<
 = 2,04; Т.о.
время
однородно
= 2,04; Т.о.
время
однородно
сравнение и однородность Задача 2
Экспериментально установлено время снятия всасывающего рукава диаметром 125 мм. с МСП.
Требуется:
определить требуемое количество измерений для исполнителя № 1;
сравнить дисперсии и среднее время двух исполнителей и провести их анализ.
I.
Требуемое
количество измерений nтр=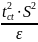 =
= ≈ 253
> nфакт=17,
где
≈ 253
> nфакт=17,
где
=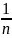
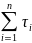 =
=
 *111,3
= 6,55 – среднее арифметическое исполнителя
№ 1
*111,3
= 6,55 – среднее арифметическое исполнителя
№ 1
= = (735,5) = 43.26 – дисперсия исполнителя № 1
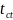 =1,96
– коэффициент Стьюдента, с доверительной
вероятностью 0,95;
=1,96
– коэффициент Стьюдента, с доверительной
вероятностью 0,95;
ε = 0,1∙ = 0,655 - ошибка эксперимента.
II.
2 = = *113.2 = 6,66 – среднее арифметическое исполнителя № 2
= = (761.7) = 44.8 – дисперсия исполнителя № 2
