ОСНОВЫ ТЕРМОДИНАМИКИ

Закон о равномерном распределении энергии

по степеням свободы молекул. Внутренняя энергия

идеального газа

Внутренняя энергия U термодинамической системы является функцией состояния и характеризует энергию теплового движения и энергию взаимодействия микрочастиц системы (молекул и атомов). Пренебрегая потенциальной энергией взаимодействия, внутреннюю энергию одного моля идеального газа можно представить как

,

где – средняя кинетическая энергия теплового движения молекулы; – число Авогадро, характеризующее количество молекул в одном моле газа.

Выражение для внутренней энергии одного моля идеального одноатомного газа будет иметь вид

Число независимых координат, полностью определяющих положение материальной точки или системы в пространстве, называется числом степеней свободы. Так как молекулу одноатомного газа можно рассматривать как материальную точку, положение которой в пространстве полностью определяется тремя координатами (x, y, z), то она имеет три степени свободы ( ) поступательного движения.

Молекула двухатомного газа рассматривается как две жестко связанные материальные точки и имеет 5 степеней свободы, т.е. кроме трех поступательных есть еще две вращательные относительно осей x и z .

Трех- и многоатомные молекулы имеют 6 степеней свободы (три поступательных и три вращательных).

Согласно закону Больцмана внутренняя энергия распределяется равномерно по степеням свободы молекул; на каждую степень свободы приходится кинетическая энергия теплового движения, равная .

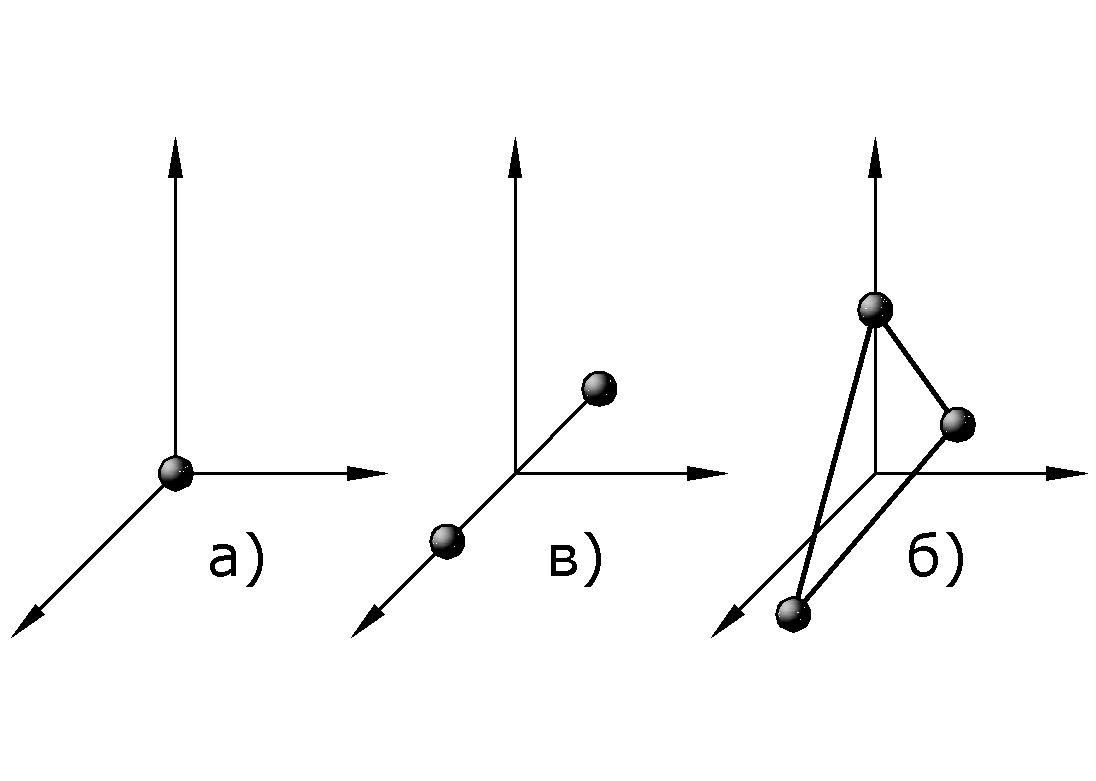
	где i – число степеней свободы.
Рис.

Внутренняя энергия любой массы газа равна кинетической энергии теплового движения молекул и определяется как

Первое начало термодинамики

Рассмотрим термодинамическую систему (газ), внутренняя энергия которой U изменяется за счет совершения над системой работы A и за счет сообщения ей некоторого количества теплоты Q.

Первое начало термодинамики утверждает (на основе обобщения многовековых опытных данных), что

Формулу можно переписать в виде

теплота, сообщенная системе, расходуется на увеличение ее внутренней энергии и на совершение работы против внешних сил. Для малых изменений системы имеем

Если термодинамическая система периодически возвращается в исходное состояние, то изменение внутренней энергии равно нулю ( ), и вся подведенная к системе теплота может быть, согласно первому началу термодинамики, переведена в работу . Причем, нельзя построить периодически действующий двигатель, который совершал бы работу, большую, чем количество сообщающейся ему извне энергии, или невозможен вечный двигатель 1-го рода.

Первое начало термодинамики – это закон сохранения энергии в термодинамике.

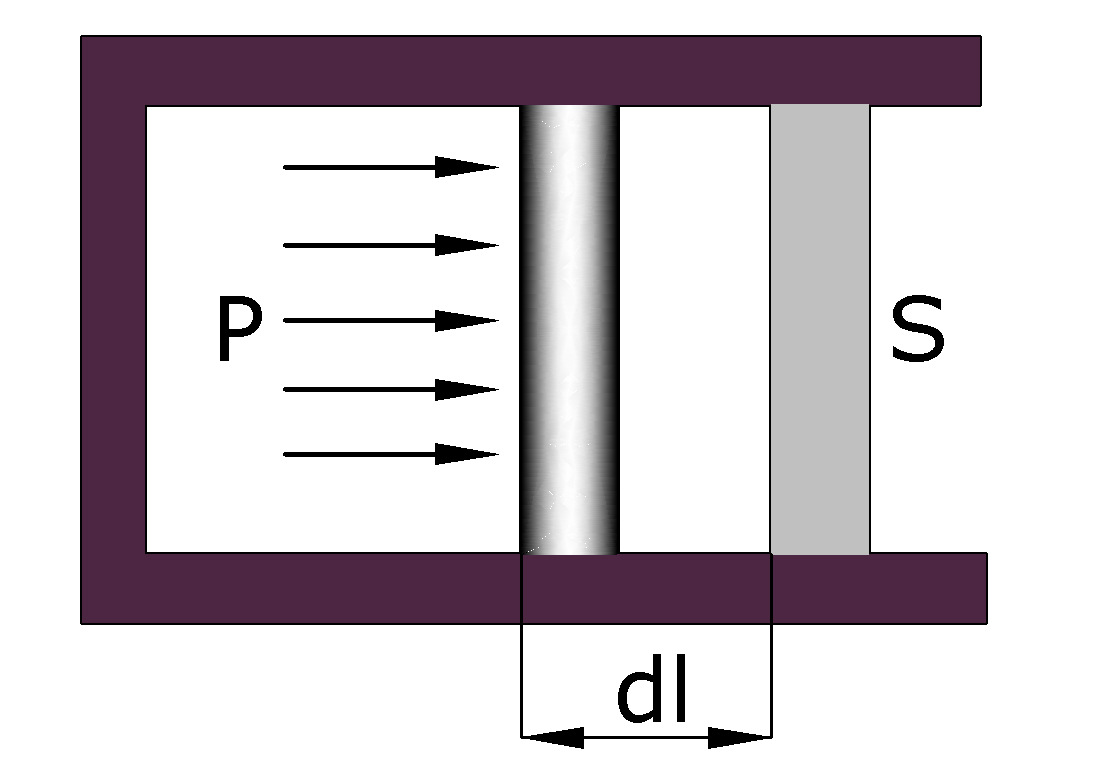
Работа газа при изменении его объема

Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде.

Газ, расширяясь, передвигает поршень на расстояние dl и производит работу

где – площадь поршня; – изменение объема.

Таким образом, работа при расширении газа определяется как

	Работа в процессе 1–2 интегрирование формулы
Рис.

При расширении газа работа положительна , то есть газ совершает работу, при сжатии , т. е. работа совершается над газом.

Теплоемкость идеального газа

Удельная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 кг вещества на 1 к и определяется как

Молярная теплоемкость – величина, равная количеству теплоты, необходимому для нагревания 1 моля на 1 к

где – число молей.

Удельная теплоемкость связана с молярной теплоемкостью соотношением:

где М – молекулярная масса.

Найдем выражения для молярной теплоемкости в изохорном и изобарном процессах. Для этого запишем первое начало термодинамики для 1-го моля газа

При V = const все сообщенное газу тепло идет на увеличение его внутренней энергии, т. е.

При из

из уравнения Клапейрона – Менделеева имеем

Уравнения Майера

Таким образом, теплоемкость в изобарном процессе равна

Из формулы следует, что всегда больше на величину газовой постоянной R. Это объясняется тем, что при нагревании газа при постоянном давлении требуется дополнительное количество теплоты на совершение работы расширения газа. Отсюда вытекает физический смысл универсальной газовой постоянной R – это работа, которую надо совершить при изобарическом нагревании 1 моля газа на 1 К.

Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме можно выразить как

Применение I начала термодинамики к изопроцессам

Среди равновесных процессов, происходящих в термодинамических системах (газах), выделяют изопроцессы, при которых один из параметров состояния остается постоянным.

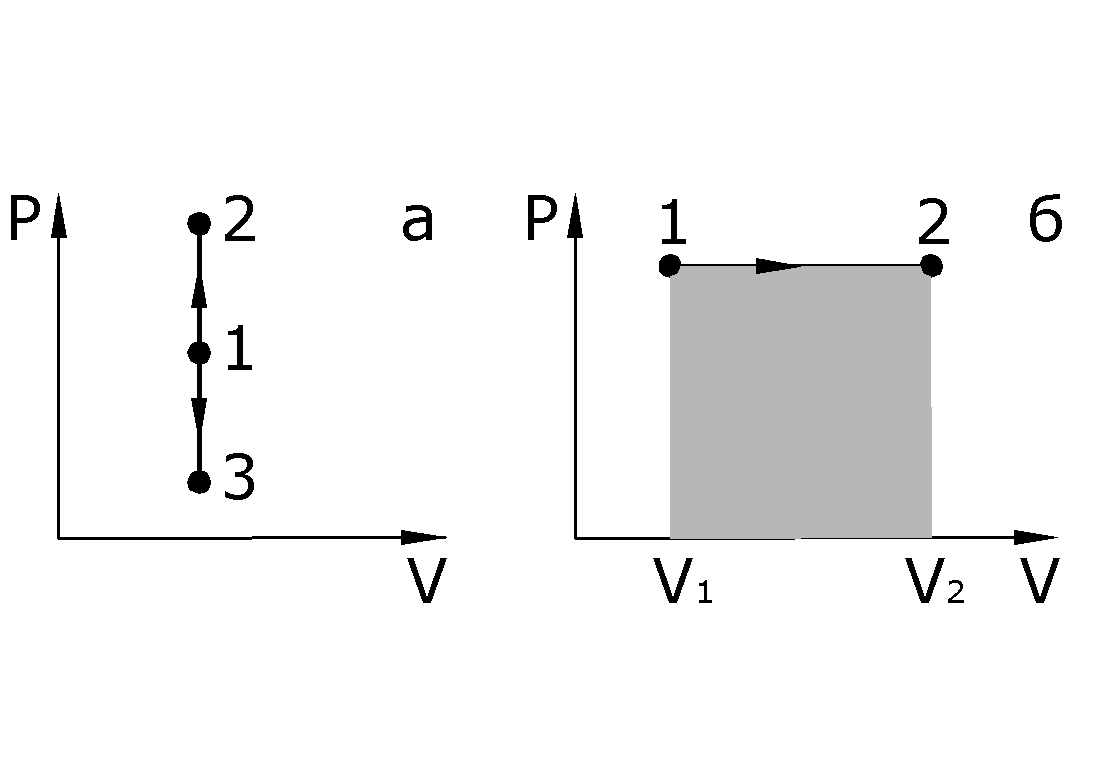
Изохорный процесс (V = const). В координатах P, V изохорный процесс изображается прямой параллельной оси ординат (рис. 6.3, а). В изохорном процессе газ не совершает работы, т. е. . Тогда из первого начала термодинамики количество теплоты выражается зависимостью вида:

	Таким образом, в изохорном процессе все тепло, сообщенное газу, идет на увеличение его внутренней энергии.
Рис.

Изобарный процесс (P = const). Диаграмма этого процесса (изобара) изображается прямой параллельной оси x. Работа при расширении газа от V₁ до V₂ определяется как

Работа численно равна площади заштрихованного прямоугольника на рис. Если воспользоваться уравнением Менделеева – Клапейрона ( ), откуда следует, что ,

С учетом полученных выражений первое начало термодинамики для изобарного процесса в дифференциальной форме можно представить в виде

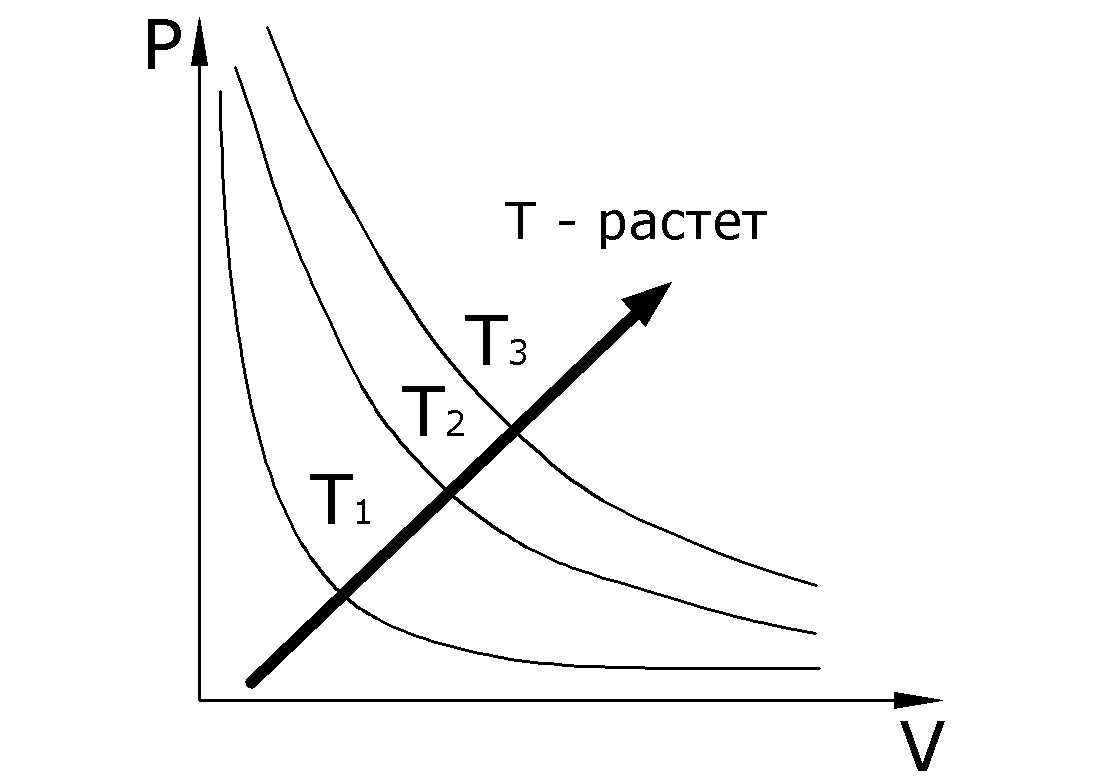
Изотермический процесс (T = const). Уравнением изотермического процесса является закон Бойля-Мариотта

Диаграмма изотермического процесса приведена на рис.

Работа в изотермическом процессе (T = const) может быть определена как

Рис. 6.4

Согласно первому началу термодинамики так как при В изотермическом процессе все количество теплоты, сообщаемое газу, расходуется им на совершение работы против внешних сил

Теплоемкость изотермического процесса стремится к бесконечности, т. е.