Розв’язок

Перша частина наданої задачі розглянута у прикладі 1.1, у розв’язку якого знайдений склад механізму ( ; ; ) і визначений ступінь його рухомості .У наданої схеми відсутні вищі кінематичні пари, немає ланок, які створюють пасивні зв’язки або надлишкові (зайві) ступені свободи . Зазначену на схемі (рис. А, Б) вхідну ланку 1 включено до складу початкового механізму першого класу.

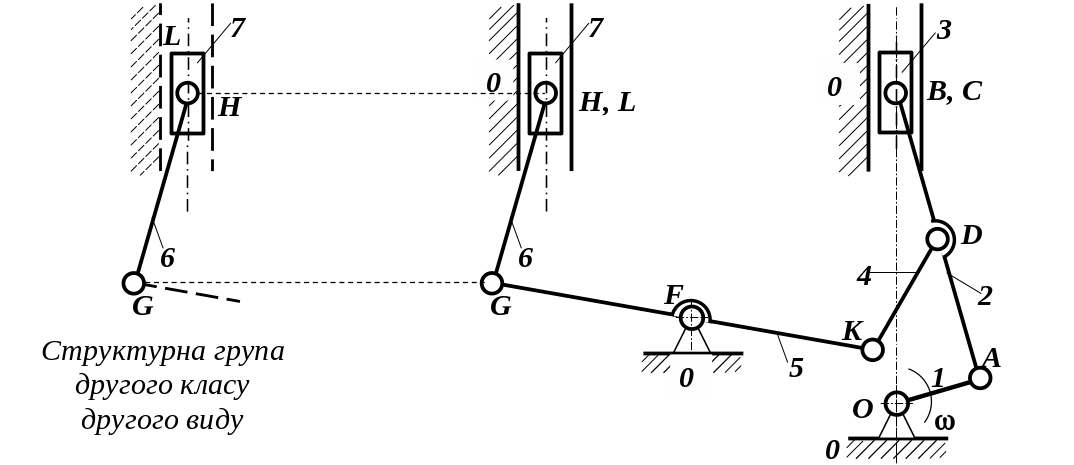
Структурний аналіз починається з видалення першої групи ланок 6-7 (рис. Д).

Їх відокремлення зі складу механізму не порушує цілісності першого залишкового механізму. Цей і наступні процеси роз’єднання вихідного механізму послідовно вказані на рис.  Д і Е. Після першого відокремлення у механізму залишились п’ять рухомих ланок і сім кінематичних пар п’ятого класу (рис. К). Ступінь рухомості першого залишкового механізму не змінилась, тобто . Після другого відокремлення маємо (рис. Ж) у залишковому механізмі ; . Ступінь рухомості , не змінилась. Як у першому випадку, це вказує на слушність відокремлення груп ланок.

Рис. Д. Процес вилучення першої групи ланок зі складу наданої кінематичної схеми

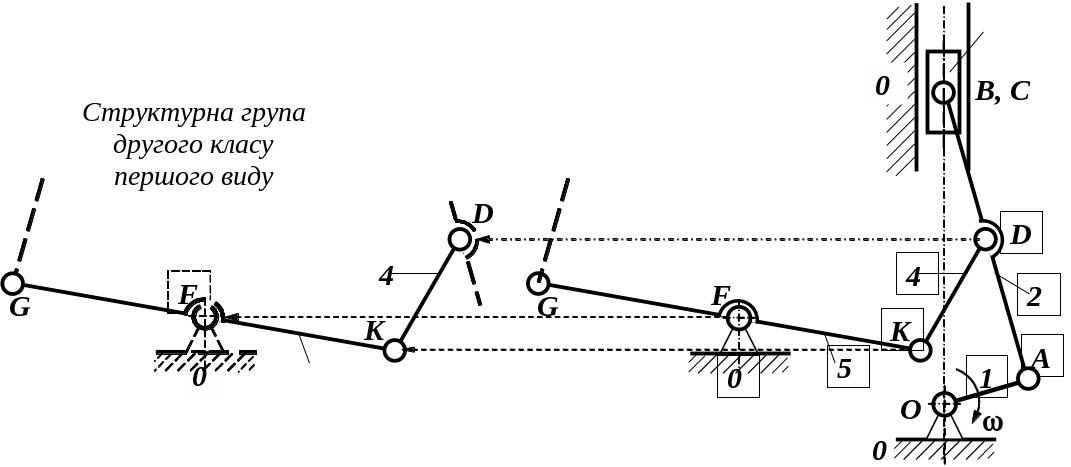
Рис. Е. Відокремлення другої групи ланок

Після відокремлення останньої групи залишається тільки початковий механізм першого класу (рис. З).

Рис. Ж. Відокремлення третьої групи ланок

Всі групи ланок належать до другого класу і другого порядку. Формула будови механізму має наступний вигляд . За її складом вихідний механізм є механізмом другого класу.

Повна відповідь: ; Формула будови . Механізм другого класу.

Структурну класифікацію важільних механізмів можна також застосовувати при класифікації плоских механізмів із вищими кінематичними парами. З цією метою у них вищі пари попередньо замінюються відповідними ланцюгами з парами V класу.

7. Заміна вищих кінематичних пар

Для перенесення структурної класифікації важільних механізмів (ланки яких з’єднуються тільки нижчими парами) на механізми з вищими парами вдаються до заміни вищих пар нижчими. Для спрощення кінематичного і динамічного дослідження плоских механізмів у багатьох випадках доцільно замінити механізм із вищими парами IV класу еквівалентним механізмом з нижчими парами V класу. При подібній заміні кінематичний ланцюг з нижчими парами повинен бути структурно і кінематичне еквівалентним заміненій парі IV класу.

Умовою структурної еквівалентності є те, що умовний кінематичний ланцюг, що її замінює, повинен накладати на відносний рух ланок стільки умов зв’язку, скільки накладає вища пара IV класу. Кожна кінематична пара IV класу в плоскому механізмі накладає на відносний рух ланок одну умову зв’язку. Отже, і кінематичний ланцюг, що її замінює, складається з p₅ пар V класу і n рухомих ланок і повинен накладати одну умову зв’язку, тобто . Звідси випливає, що співвідношення між числом пар V класу і числом ланок у заміненому ланцюзі, буде відповідати залежності

. (1.2)

Найменше число пар, яке відповідає цій умові, дорівнює двом при n = 1, отже найпростішою заміною вищої пари є ланка з двома парами V класу.

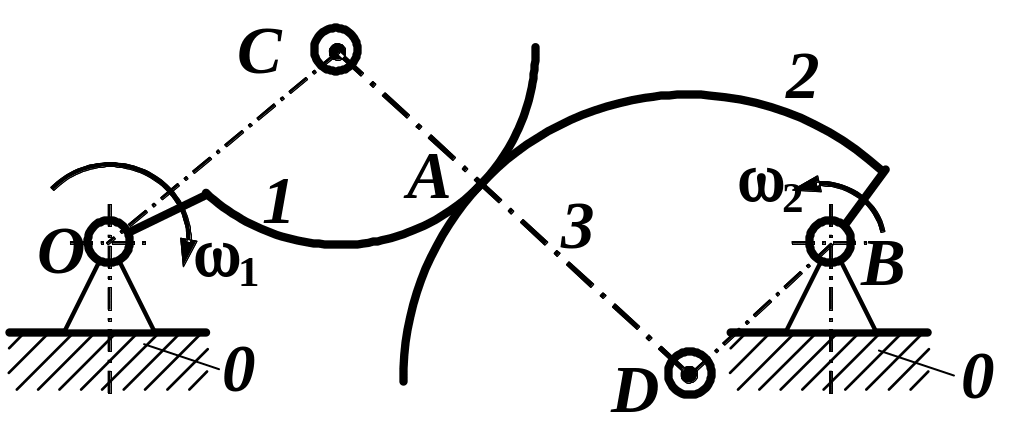
Умовою кінематичної еквівалентності буде збереження кінематичних характеристик відносного руху ланок (рис. 1.13). Для здійснення такої заміни вищої пари застосуємо наступну властивість контактуючих кривих: коло кривини в точці дотику кривої і сама крива еквівалентні до похідних другого порядку включно.

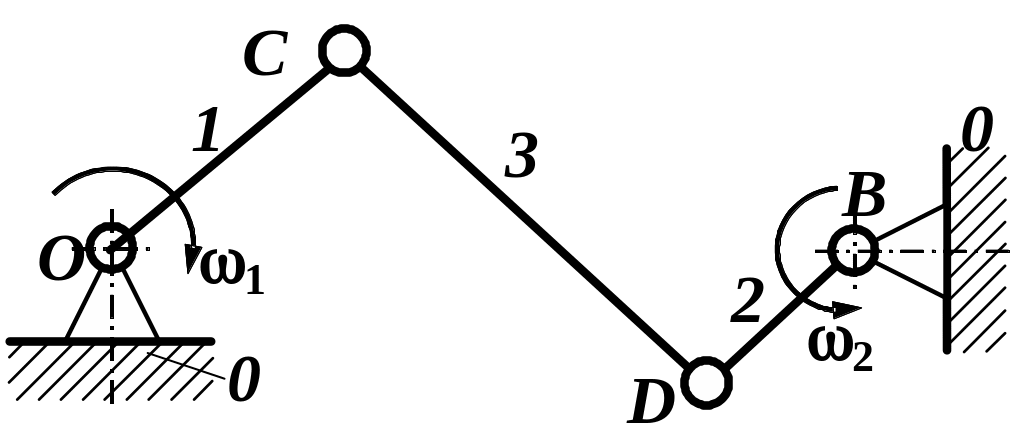
Виходячи з обох умов, в центрах кривини контактуючих кривих O₁ і O₂ слід розмістити кінематичні пари V класу, з’єднавши їх між собою фіктивною ланкою 3 (рис. 1.13, а). Одержаний таким способом замінюючий механізм (рис. 1.13, б), є миттєвим механізмом. Він має змінні розміри ланок, яки залежать від положення ланок механізму з вищою парою.

а

б

Рис. 1.13. Заміна вищих кінематичних пар