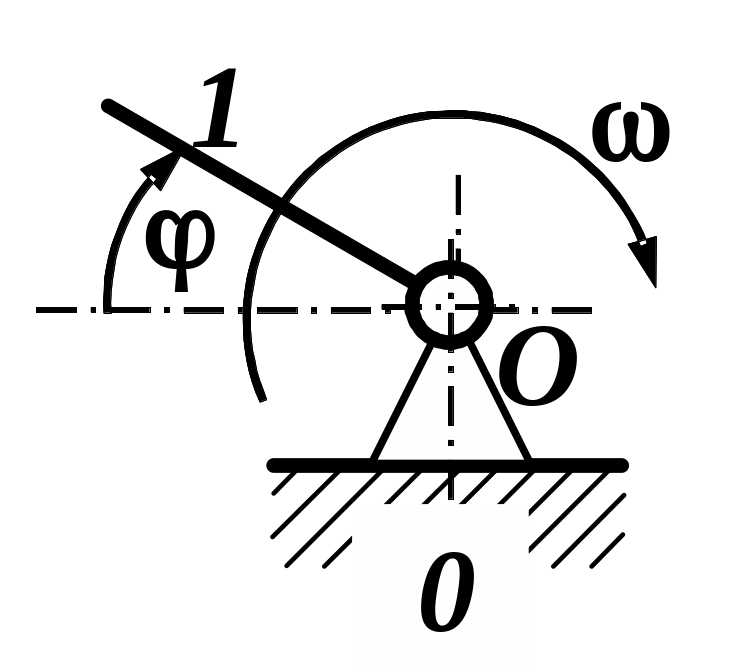5. Зайві ступені свободи

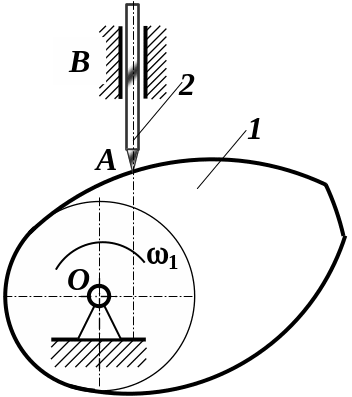
У плоскому кулачковому механізмі, (рис. 1.6, а), якщо вважати, що ролик 3 жорстко зв'язаний зі коромислом 2, то ступінь рухомості .

а

б

в

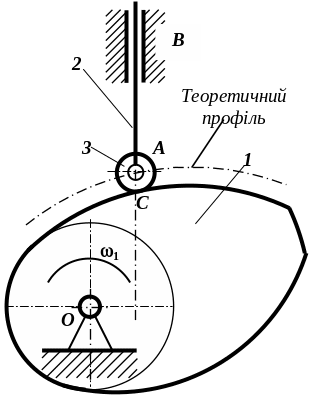
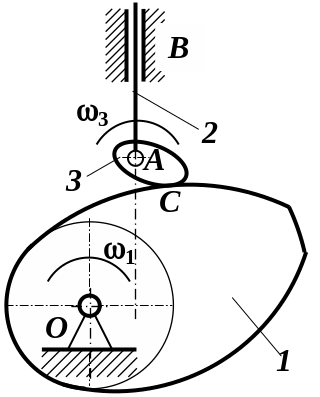
Рис. 1.6. Кулачковий механізм із зайвим ступенем рухомості (а), з двома ступенями (б) і з теоретичним профілем

Але, якщо вважати ролик вільно обертовим, то формальний розрахунок приведе до результату , тобто ролик вносить зайвий ступінь свободи . Але, фактично при підрахунку ступеня рухомості механізму, цей обертальний рух не повинен прийматися до уваги. Цей ступінь може бути реалізованим тільки у випадках, коли форма ролика не буде ідеальною круглою, або вісь обертальної пари не співпадатиме з центром кола (рис. 1.6, б).

При теоретичному дослідженні механізмів з зайвими ступенями свободи робочий профіль замінюється на теоретичний (рис. 1.6, в), який співпадає з траєкторією зворотного руху ролика 3 навколо нерухомого робочого профілю (вказано штрих пунктиром на рис. 1.6, а).

Визначимо ступень рухомості механізму на прикладі розрахунку механізму обчислювання синусів кутів.

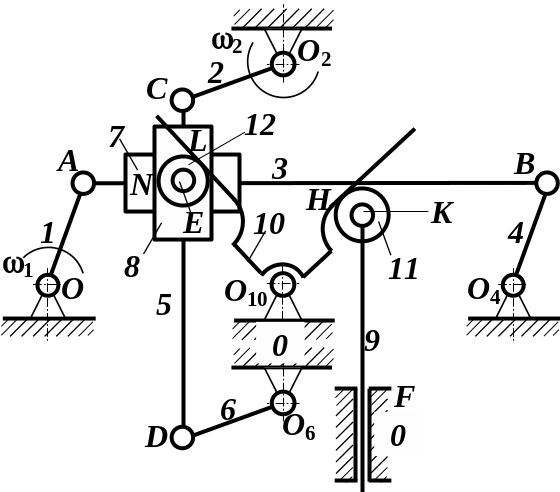
Приклад 1.2. Для заданого механізму (рис. В) визначити за структурною формулою Чебишева (1.3) ступінь свободи. При наявності ланок, що створюють пасивні зв’язки або надлишкові (зайві) ступені свободи , вказати їх і, після вилучення зі складу механізму, підрахувати дійсний ступінь свободи .

Рис. В. Механізм обчислювання відношення синусів кутів

Розв’язок

Перш за все визначимо склад наданого механізму. До нього входять: стійка 0, кривошипи 1, 2, 4, 6, шатуни 3, 5, коромисло 10, повзуни 7, 8, 9, ролики 11 і 12. загальна кількість ланок , рухомих ланок . Усі ланки між собою з’єднані наступними кінематичними парами:

• обертальні пари або шарніри: O, O₂, O₄, O₆, O₁₀, A, B, С, D, E (2 шарніра, між повзунами 7 і 8, та між повзуном 8 і роликом 12) і K;

• поступальні пари: F, N (2 пари, 7-3 і 8-5);

• вищі пари четвертого класу L і H.

Обертальні та поступні пари належать за кількістю зв’язків до п’ятого класу. Таким чином, маємо ; . За формулою Чебишева підрахуємо ступінь свободи механізму .

Але два ролика 11 і 12, яки входять до складу механізму, утворюють два ступеня свободи місцевого характеру, що не впливають на закон руху вихідної ланки 9. Тому при підрахунку рухомості механізму їх необхідно вилучити з його складу. Для цього умовно будемо вважати їх жорстко пов’язаними з ланками 9 і 8. За умови цього перетворення маємо ; ; . Дійсний ступінь свободи механізму дорівнює . Для забезпечення роботи механізму у відповідності до цього результату надається рух двом ланкам, 1 і 2.

Повна відповідь: ; ; ; .

6. Принцип створювання плоских механізмів

В теорії механізмів і машин замість конструктивних креслень використовуються умовні зображення – кінематичні схеми, які не залежать від функціональних особливостей механізмів. Їх створюють за структурною класифікацією механізмів.

За цією класифікацією найпростіший однорухомий механізм, що складається з двох ланок – стояка і рухливої ланки, названо первинним механізмом або механізмом першого класу (рис.1.7). В основному, як правило застосовується механізм з кривошипа і стійки (рис.1.7, а). У таких механізмах немає ведених ланок, тому немає передачі і перетворення руху. Це механізми роторних приладів і машин (гіроскопів, електродвигунів і генераторів, турбін, насосів, вентиляторів і ін.). Будь-якій плаский механізм можна створити шляхом приєднання до одного або декількох первинних механізмів одного або декількох кінематичних ланцюгів, які називаються групами Ассуру.

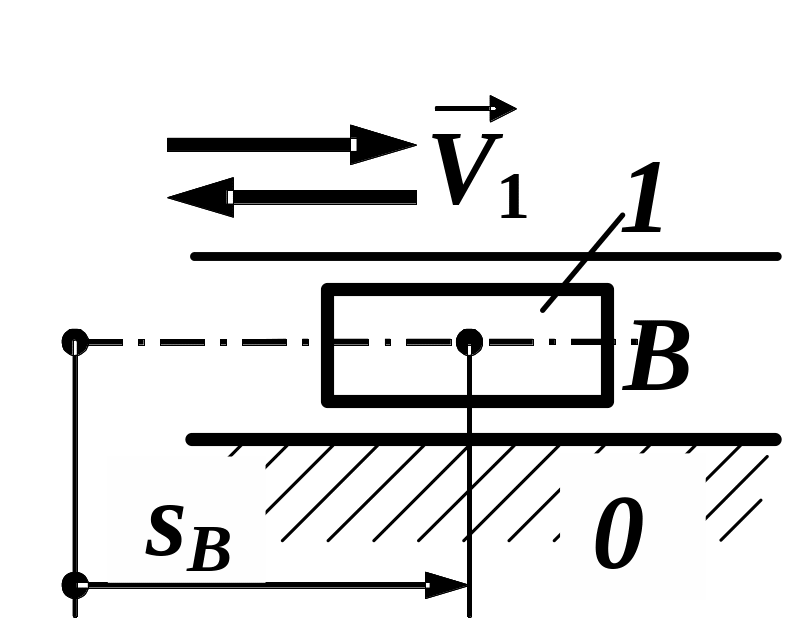
Рис. 1.7. Механізми першого класу з обертальною (а) і поступальною (б) кінематичними парами

а

б

Кількість початкових механізмів у складі кінематичного ланцюга дорівнює кількості ступенів свободи механізму. Основний принцип створювання механізмів за Ассуром виходить з того, що ступінь рухомості кінематичного ланцюга не змінюється від приєднання або видалення з нього іншого ланцюга з нульовою рухомістю . Рухомость створеного механізму запишеться як сума (рис. 1.8).

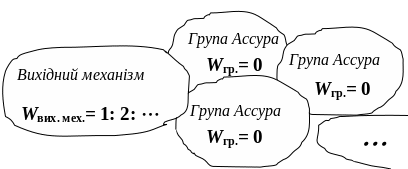
Рис. 1.8. Створення складного механізму за принципом Ассура