- •Збірник
- •Структурна класифікація плоских механізмів
- •Загальні поняття і визначення
- •Класифікація кінематичних пар
- •Ступінь рухомості механізму
- •Розв’язання
- •Надлишкові (пасивні) зв'язки
- •Зайві ступені свободи
- •Розв’язок
- •Принцип створювання плоских механізмів
- •Групи Ассуру та їх класифікація
- •Формула будови та визначення класу механізму
- •Розв’язок
- •Заміна вищих кінематичних пар
- •Послідовність виконання структурного аналізу плоских механізмів
- •Питання для самоконтролю
- •Передаточні механізми
- •Класифікація багатоланкових передаточних механізмів
- •Передаточне відношення багатоланкової передачі
- •Передаточне відношення передачі з нерухомими осями
- •Виготовлення зубчастих коліс
- •2.4.1. Підрізування та загострення зубів
- •Передаточні механізми з рухомими осями
- •2.5.1. Передаточні відношення планетарних механізмів
- •Розв’язок
- •2.5.2. Умови синтезу планетарних передач
- •Питання для самоконтролю
- •Динаміка машинних агрегатів
- •Класифікація навантажень ланок механізмів
- •Задачі силового аналізу механізмів
- •Метод зведення
- •Рівняння руху ланки зведення
- •Режими руху машинного агрегату
- •Механічний коефіцієнт корисної дії
- •Визначення потужності та вибір двигуна
- •Питання для самоконтролю
Ступінь рухомості механізму
Механізмом називають кінематичний ланцюг з нерухомою ланкою, у якому при заданому русі однієї або декількох ланок щодо будь-якої з них всі інші ланки роблять однозначно обумовлені рухи.
Кількість узагальнених координат, що цілком характеризують положення, а отже, і рух тіла або механізму, прийнято називати числом ступенів свободи (ступенем рухомості ) тіла або механізму.
Для плоских механізмів кількість ступінь рухомості визначається за структурною формулою П.Л. Чебишева
![]() . (1.1)
. (1.1)
де
![]() – кількість рухомих ланок;
– кількість рухомих ланок;
![]() і
і
![]() –
кількість кінематичних пар, відповідно
IV
і V
класів.
–
кількість кінематичних пар, відповідно
IV
і V
класів.
Визначимо ступень рухомості механізму на конкретному прикладі.
Приклад 1.1.
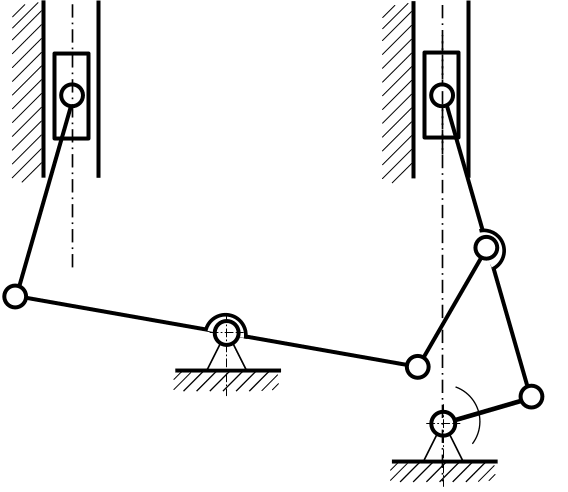
Визначити ланки і кінематичні пари механізму Дизеля (рис. А). Підрахувати за структурною формулою Чебишева ступінь рухомості.
Рис. А. Схема механізму Дизеля без позначень ланок і кінематичних пар |
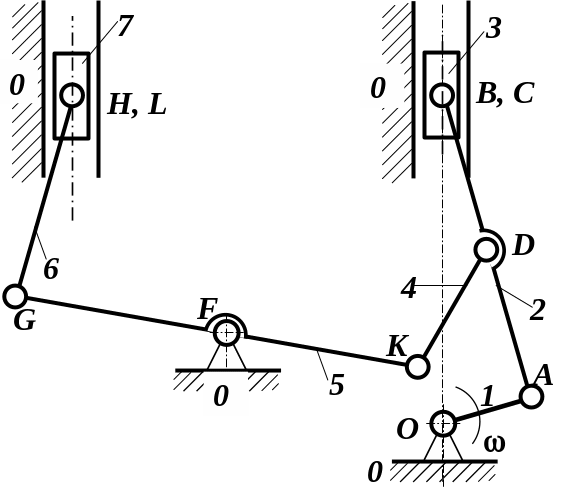
Рис Б. Схема механізму Дизеля з позначками ланок і кінематичних пар |
Розв’язання
Розв’язання задачі розпочнемо з визначення ланок і кінематичних пар (рис. А). До складу наданої схеми належать: стійка 0, кривошип 1, шатуни 2, 4, 6, коромисло 5, повзуни 3 і 7. Усі ланки позначені на схемі арабськими цифрами (рис. б). Окрім стійки 0, усі інші ланки є рухомими.
Таким чином, кількість
рухомих ланок у наданій схемі дорівнює
![]() .
Ланки механізму з’єднані між собою
наступними кінематичними парами:
обертальні пари або шарніри O,
A,
B,
D,
K,
F,
G,
H;
поступальні пари C
і L
(рис. Б).
.
Ланки механізму з’єднані між собою
наступними кінематичними парами:
обертальні пари або шарніри O,
A,
B,
D,
K,
F,
G,
H;
поступальні пари C
і L
(рис. Б).
Усі перелічені пари належать
до п’ятого класу за кількістю обмежень,
їх загальна кількість
![]() .
Кінематичні пари четвертого класу у
наданої схемі відсутні,
.
Кінематичні пари четвертого класу у
наданої схемі відсутні,
![]() .
Підрахуємо ступінь рухомості за
структурною формулою Чебишева
.
Підрахуємо ступінь рухомості за
структурною формулою Чебишева
![]() .
.
Отже механізм має один ступінь свободи .
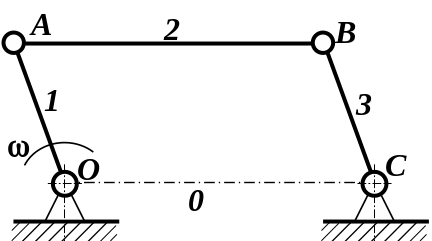
Надлишкові (пасивні) зв'язки
Крім зв’язків, що активно впливають на характер руху механізмів, у них можуть зустрітися умови зв'язку і ступені свободи , що не роблять ніякого впливу на рух ланок механізму в цілому. Вилучення з механізмів ланок і кінематичних пар, яким ці ступені свободи і умови зв’язку належать, може бути зроблене без зміни загального характеру руху механізму в цілому. Такі зв’язки називаються надлишковими або пасивними зв’язками, а ступені свободи – зайвими ступенями свободи .
Іноді
зайвий зв`язок свідомо впроваджують до
складу механізму для підвищення його
жорсткості або для усунення невизначеності
руху ланок в деяких положеннях. Включення
до складу механізму таких ланок повинно
відбуватися з виконанням додаткових
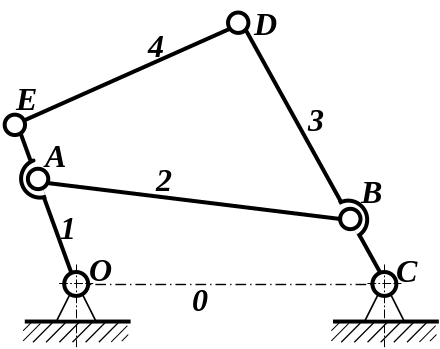
умов. Наприклад, ланка 4
входить до складу шарнірного механізму
при виконанні
додаткових умов
![]() і
і
![]() (рис.1.5, б).
Дійсно, ступінь рухомості механізму з
ланкою 4
згідно розрахунку
(рис.1.5, б).
Дійсно, ступінь рухомості механізму з
ланкою 4
згідно розрахунку
![]() дорівнює нулю. Цей результат відповідає
дійсності тільки відносно статично
визначеної ферми (рис.1.5, а),
яку побудовано без утримання згаданих
умов. Але при виконанні додаткових умов
і
ланка 4
тільки дублює зв’язки ланки 2
і не створює перешкод руху інших ланок,
тобто накладає на рух механізму умови
зв’язку, що є надлишковими.
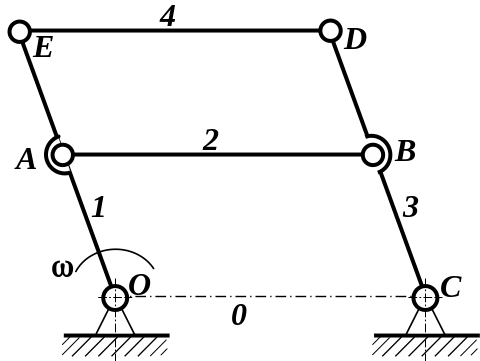
З приводу цього при теоретичному
дослідження вона повинна бути відкинута.
Тільки вилучивши з механізму надлишкову
ланку з двома кінематичними парами,
отримаємо шарнірний паралелограм (рис.
1.5, в)
з одним ступенем свободи ,
дорівнює нулю. Цей результат відповідає
дійсності тільки відносно статично
визначеної ферми (рис.1.5, а),
яку побудовано без утримання згаданих
умов. Але при виконанні додаткових умов
і
ланка 4
тільки дублює зв’язки ланки 2
і не створює перешкод руху інших ланок,
тобто накладає на рух механізму умови
зв’язку, що є надлишковими.
З приводу цього при теоретичному
дослідження вона повинна бути відкинута.
Тільки вилучивши з механізму надлишкову
ланку з двома кінематичними парами,
отримаємо шарнірний паралелограм (рис.
1.5, в)
з одним ступенем свободи ,
![]() .
.
а |
б |
в |
Рис. 1.5. Багатоланкові шарнірні конструкції
а – статично визначена ферма; б – шарнірний паралелограм з пасивними зв’язками; в – шарнірний паралелограм