4. Рівняння руху ланки зведення

Аналітична залежність між діючими на ланки навантаженнями і кінематичними параметрами руху називається рівнянням руху. Після визначення характеристик (3.1) і (3.2) складається рівняння руху ланки зведення у енергетичної або диференціальної формі. Закон, одержаний при розв’язанні рівняння руху ланки зведення, співпадає із законом руху вхідної ланки.

Запишемо рівняння зміни кінетичної енергії ланки зведення в довільному інтервалі часу : , де – поточне значення кінетичної енергії; – значення кінетичної енергії на початку інтервалу; – повна робота зведених навантажень; – робота зведених рушійних навантажень; – робота зведених навантажень опору. Значення усіх чинників рівняння ланки зведення мають наступний вигляд: ; ; ; 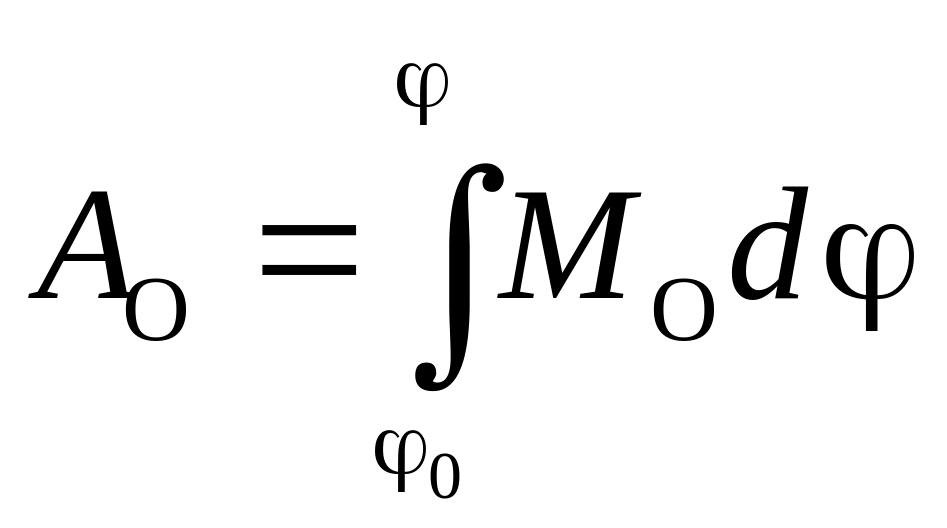, де і – значення зведеного моменту інерції та кутової швидкості на початок розглянутого проміжку часу.

З урахуванням вказаних залежностей, рівняння руху ланки зведення в енергетичної формі набуває наступного вигляду

. (3.3)

З рівняння (3.3) отримаємо залежність для визначення кутової швидкості ланки зведення

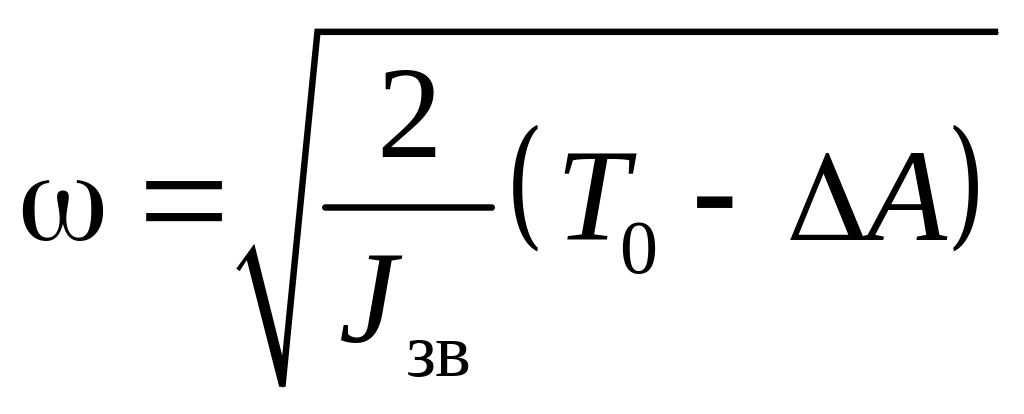(3.4)

Отримана залежність має неявний вигляд, оскільки обидві частини рівняння залежать від узагальненої координати , що не дає можливості отримати аналітичне розв’язання рівняння (3.3). Закон руху вхідної ланки на підставі рівняння (3.3) визначається графоаналітичними методами.

Рівняння руху ланки зведення у диференціальної формі має вигляд

. (3.5)

Рівняння (3.5) у загальному випадку є нелінійним диференціальним рівнянням, розв’язання якого може бути виконаним тільки наближеними методами. Рішення для окремих випадків наведені у навчальної літературі, наприклад у посібнику [4].

5. Режими руху машинного агрегату

Робота машинного агрегату с початку пуску до його повної зупинки поділяється на перехідні, або змінні (позначені непарними номерами) та усталені режими (рис.3.4).

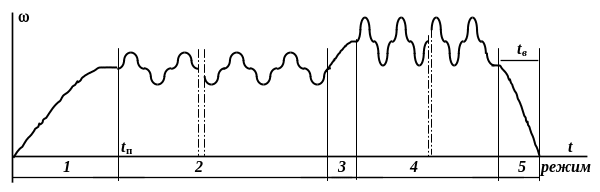
Рис. 3.4. Тахограма машинного агрегату

Змінні режими із зростанням швидкості руху – це режими розгону, а із зменшенням швидкості називаються режимами гальмування. Режим розгону із нульовою початковою швидкістю називається режимом пуску, режим гальмування з нульовою кінцевою швидкістю – режимом вибігу.

У режимах розгону робота рушійних сил більш, ніж робота сил опору, , ланки пришвидшуються, рух машинного агрегату є неусталеним. На відміну від розгону, при гальмуванні , ланки уповільнюються, рух також є неусталеним.

Під час усталеного руху усі кінематичні параметри циклічно повторюються (рис. 3.5). Сумарна робота зовнішніх сил за цикл дорівнює нулю, . Коливання кутової швидкості вхідної ланки оцінюється коефіцієнтом нерівномірності руху

, (3.6)

де 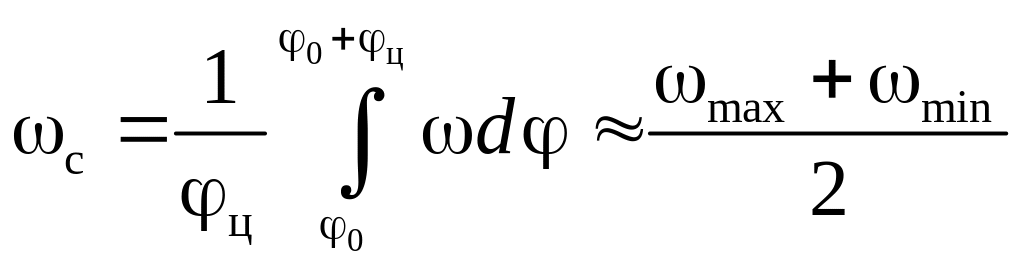– середня кутова швидкість за цикл; – кут обертання вхідної ланки, протягом якого кінематичні параметри приймають початкові значення. Для переважної більшості машинних агрегатів кінематичний цикл виконується протягом одного оберту вхідної ланки, тобто .

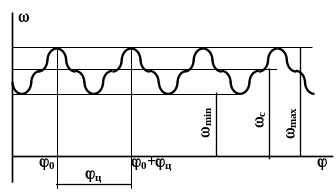
Рис. 3.5. Коливання кутової швидкості вхідної ланки на усталеному режимі роботи

Нерівномірність обертання шкідливо впливає на роботу машинного агрегату, оскільки виникають додаткові інерційні навантаження, що може призвести до поломки машини. Регулювати значення коефіцієнта нерівномірності руху можна шляхом збільшення величини моменту інерції ланки зведення. З цією метою на вал вхідної ланки встановлюється додаткова масивна деталь обертання – махове колесо.

Неперіодичні коливання швидкості на різних режимах роботи регулюються за допомогою пристроїв, що впливають на органи, яки подають енергію до вхідної ланки (приклад – відцентровий регулятор).