- •Збірник
- •Структурна класифікація плоских механізмів
- •Загальні поняття і визначення
- •Класифікація кінематичних пар
- •Ступінь рухомості механізму
- •Розв’язання
- •Надлишкові (пасивні) зв'язки
- •Зайві ступені свободи
- •Розв’язок
- •Принцип створювання плоских механізмів
- •Групи Ассуру та їх класифікація
- •Формула будови та визначення класу механізму
- •Розв’язок
- •Заміна вищих кінематичних пар
- •Послідовність виконання структурного аналізу плоских механізмів
- •Питання для самоконтролю
- •Передаточні механізми
- •Класифікація багатоланкових передаточних механізмів
- •Передаточне відношення багатоланкової передачі
- •Передаточне відношення передачі з нерухомими осями
- •Виготовлення зубчастих коліс
- •2.4.1. Підрізування та загострення зубів
- •Передаточні механізми з рухомими осями
- •2.5.1. Передаточні відношення планетарних механізмів
- •Розв’язок
- •2.5.2. Умови синтезу планетарних передач
- •Питання для самоконтролю
- •Динаміка машинних агрегатів
- •Класифікація навантажень ланок механізмів
- •Задачі силового аналізу механізмів
- •Метод зведення
- •Рівняння руху ланки зведення
- •Режими руху машинного агрегату
- •Механічний коефіцієнт корисної дії
- •Визначення потужності та вибір двигуна
- •Питання для самоконтролю
2.4.1. Підрізування та загострення зубів
Рис.2.6. Явища підрізування та загострення зуба |
При
нарізанні нормальних зубчастих коліс
з числом зубів
|
Щоб
уникнути такого небажаного явища,
необхідно
змістити рейку від центра заготовки на
величину найменшого
зміщення
![]() .
Значення
мінімального коефіцієнта
для
нормальних (нульових) зубчастих
евольвентних коліс
.
Значення
мінімального коефіцієнта
для
нормальних (нульових) зубчастих
евольвентних коліс
![]() , де
z
-
число зубів колеса, що виготовляється.
, де
z
-
число зубів колеса, що виготовляється.
На
практиці величину коефіцієнта зміщення
![]() приймають більшою від
приймають більшою від
![]() ,
але значне
збільшення
може призвести до іншого небажаного
явища – загострення зубів, при якому
товщина зуба по колу вершин
,
але значне
збільшення
може призвести до іншого небажаного
явища – загострення зубів, при якому
товщина зуба по колу вершин
![]() (рис. 2.6). Для усунення загострення зубів,
необхідно вибрати таке зміщення
інструменту, що задовольняє умову Sa
>
[Sa],
де [Sa]=(0,2...0,25)m
– допустиме значення товщини зуба по
колу вершин.
(рис. 2.6). Для усунення загострення зубів,
необхідно вибрати таке зміщення
інструменту, що задовольняє умову Sa
>
[Sa],
де [Sa]=(0,2...0,25)m
– допустиме значення товщини зуба по
колу вершин.
У коліс нарізаних зі зміщенням і без нього (рис. 2.5) однаковими залишаються такі параметри, як число зубів z, модуль m, а отже і діаметр ділильного кола d, крок зубів по ділильному колу рт, а різними - товщина зубів по ділильному колу S, ширина западини по ділильному колу e, діаметр кіл вершин d0, діаметр кіл западин df, а також співвідношення між висотою головки ha і ніжки hf зубів.
Передаточні механізми з рухомими осями
Передаточні
механізми з рухомими осями сателітів
поділяються на механізми з одним ступенем
свободи (
)
і на механізми, в яких
![]() .
Механізми одним ступенем свободи можуть
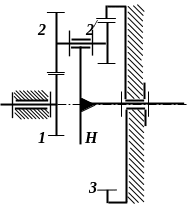
бути планетарними (рис. 2.3, в) або
замкненими диференціальними (рис.
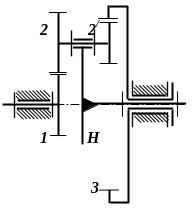
2.3, г), інші –– диференціальними
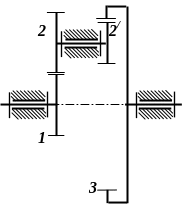
(рис. 2.3, б).
.
Механізми одним ступенем свободи можуть
бути планетарними (рис. 2.3, в) або
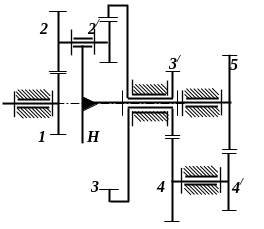
замкненими диференціальними (рис.
2.3, г), інші –– диференціальними
(рис. 2.3, б).
|
|
|
|
а |
б |
в |
г |
Рис. 2.3. Передаточні механізми: а – двохступінчаста співвісна передача; б - диференціальний механізм; в – планетарний механізм з мішаним зачепленням сателітів; г – замкнений диференціальний механізм
Планетарні зубчасті передачі дозволяють передавати більші потужності і реалізувати більші передаточні числа при меншому числі зубчастих коліс, чим передачі з нерухомими осями, через що вони набули великого поширення в сучасних машинах. За допомогою диференціальних механізмів можна передавати рух одному валу від двох або більше інших валів, які обертаються незалежно один від одного. Існує кілька методів визначення кінематичних характеристик планетарних і диференціальних механізмів, з яких розглянемо аналітичний метод, що ґрунтується на принципі оберненого руху.
В зубчастому механізмі з двома ступенями свободи (рис. 2.3, б) неможливо поставити й розв’язати задачу про визначення передаточного відношення. Можливо лише встановити зв’язок між трьома кутовими швидкостями 1, 3 і H, дві з яких незалежні. Кінематичний розрахунок механізмів з рухомими осями можна виконати із застосуванням методу інверсії або зверненого руху. У загальному випадку співвідношення між швидкостями коліс визначаються за формулою Віліса
![]() ,
(2.4)
,
(2.4)
де
![]() – передаточне відношення оберненого
механізму, який виникає з наданого
механізму при зупинці водила
– передаточне відношення оберненого
механізму, який виникає з наданого
механізму при зупинці водила
![]() ,
,
![]() – кутова швидкість ведучого валу;
– кутова швидкість ведучого валу;
![]() – кутова швидкість вихідного валу
механізму.
– кутова швидкість вихідного валу
механізму.
Таким чином для дослідження диференціального механізму з двома ступенями свободи необхідно знати дві кутових швидкості. Третю швидкість для наданої кінематичної схеми можна визначити за формулою (2.4) після розрахунку передаточного відношення оберненого механізму за відомими числами зубів коліс.