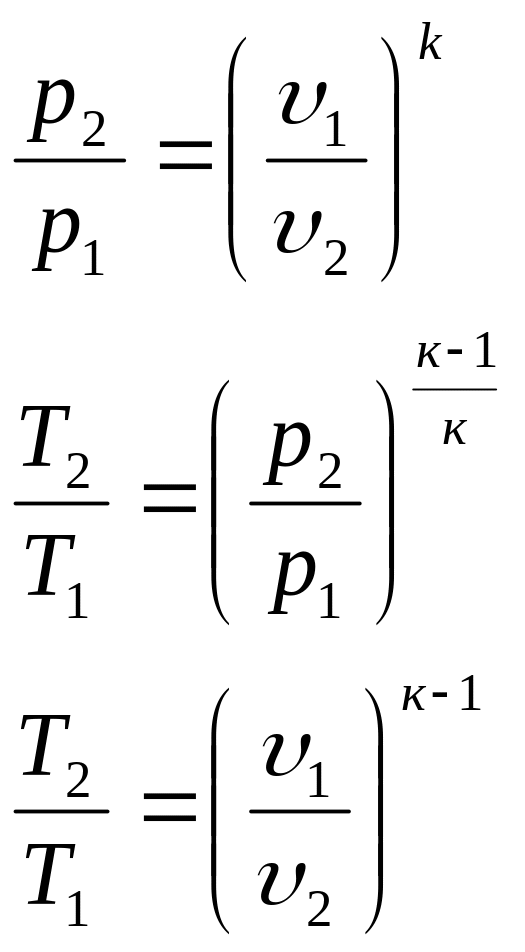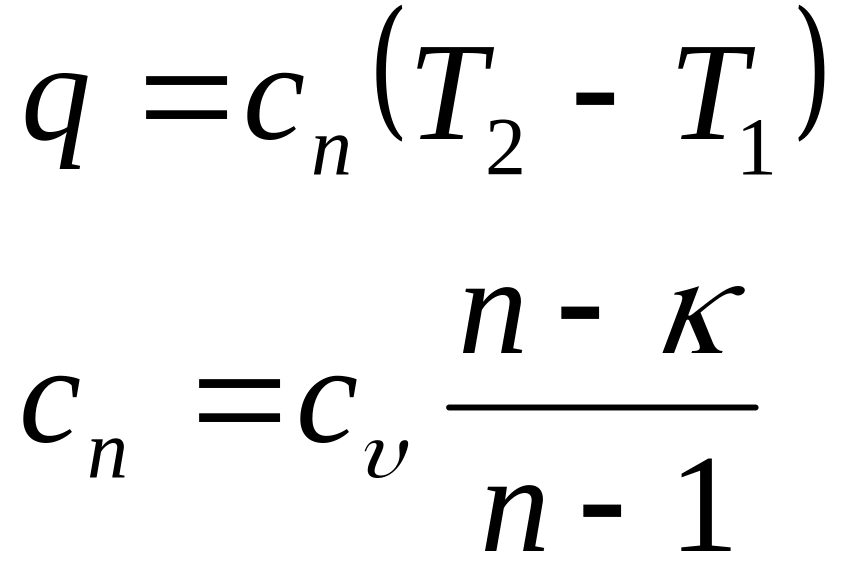- •Л.С. Коновалова, ю.А. Загромов теоретические основы теплотехники примеры и задачи
- •Введение
- •РаЗдел 1
- •1.1. Термические параметры. Уравнение состояния идеального газа
- •1.2. Смеси идеальных газов
- •1.3. Теплоемкость. Калорические параметры газов
- •1.4. Расчет параметров и процессов изменения состояния идеального газа
- •Пример расчета процесса идеального газа
- •1.5. Расчет параметров и процессов изменения состояния воды и водяного пара
- •Пример расчета процесса водяного пара с использованием таблиц
- •1.6. Истечение газов и паров из сопел
- •Задачи для самостоятельного решения
- •Методические указания к решению задач
- •1.7. Дросселирование
- •1.8. Влажный воздух
- •Задачи для самостоятельного решения
- •Методические указания к решению задач
- •1.9. Процессы компрессоров
- •Задача для самостоятельного решения
- •Контрольные вопросы по темам раздела 1
- •Раздел 2
- •2.1. Циклы теплотрансформаторов
- •2.2. Расчет обратимого цикла газового двигателя
- •2.3. Термодинамический анализ цикла энергетической газотурбинной установки гту–50–800
- •Компрессор
- •Турбина
- •Регенератор
- •2.4. Теплосиловые паровые циклы Задача для самостоятельного решения
- •Методические указания к решению задачи
- •2.5. Способы повышения кпд паротурбинных установок
- •Задачи для самостоятельного решения
- •2.5.1. Система кпд для оценки эффективности циклов паротурбинных установок
- •Методические указания к решению задач 1, 2, 3
- •2.6. Термодинамический анализ циклов холодильных установок
- •Задачи для самостоятельного решения
- •Методические указания к решению задач
- •2.7. Расчет стационарной теплопроводности и теплопередачи
- •Задачи для самостоятельного решения
- •Методические указания к решению задач №№1-5
- •2.8. Расчет нестационарной теплопроводности
- •Задачи для самостоятельного решения
- •Методические указания к решению задач №№1-5
- •Контрольные вопросы по темам радела 2
- •Раздел 3
- •3.1. Расчет теплоотдачи при естественной конвекции жидкости
- •Задачи для самостоятельного решения
- •3.2. Расчет теплоотдачи при вынужденной конвекции жидкости
- •3.2.1. Теплоотдача при вынужденном продольном омывании поверхности
- •3.2.2. Теплоотдача при вынужденном омывании труб и пучков труб поперечным потоком жидкости
- •3.2.3. Теплоотдача при вынужденном течении жидкости в трубах
- •Задачи для самостоятельной работы
- •3.3. Расчет теплоотдачи при фазовых превращениях
- •3.3.1. Теплоотдача при пленочной конденсации неподвижного пара на вертикальной поверхности
- •3.3.2. Теплоотдача при пленочной конденсации неподвижного пара на горизонтальной трубе
- •3.3.3. Теплоотдача при пленочной конденсации движущегося пара на горизонтальных трубах
- •3.3.4. Теплоотдача при пузырьковом кипении жидкости в условиях свободного движения
- •3.3.5. Теплоотдача при пузырьковом кипении жидкости в условиях вынужденной конвекции в трубах
- •Задачи для самостоятельного решения
- •3.4. Теплообмен излучением
- •3.4.1. Теплообмен излучением в системе тел с плоскопараллельными поверхностями, разделенными прозрачной средой
- •3.4.2. Теплообмен излучением между телом и его оболочкой, разделенными прозрачной средой
- •3.4.3. Особенности излучения газов и паров. Лучистый теплообмен между газом и оболочкой
- •Задачи для самостоятельного решения
- •3.5. Теплообменные аппараты
- •Задачи для самостоятельного решения
- •Методические указания к решению задач №№1 – 5
- •3.6. Расчет теплопередачи со сложным теплообменом на поверхностях
- •Задачи для самостоятельного решения
- •Методические указания к решению задач
- •Контрольные вопросы по темам раздела 3
- •Приложение
- •Литература
- •Оглавление
- •РаЗдел 1 5
- •Раздел 2 35
- •Раздел 3 72
1.4. Расчет параметров и процессов изменения состояния идеального газа
Графическое представление изобарных, изохорных, изотермических и адиабатных процессов идеального газа дано на рис. 1.1 и 1.2.
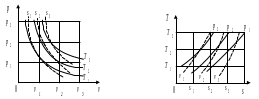 Рис. 1.1
Рис.
1.2
Рис. 1.1
Рис.
1.2
Изобары (р1, р2, р3) в T-s- диаграмме – эквидистантные логарифмические кривые.
Изохоры (υ1, υ2, υ3) в T-s- диаграмме – эквидистантные логарифмические кривые, располагаются круче изобар.
Изотермы (Т1, Т2, Т3) в р-υ-диаграмме – симметричные гиперболы (рυ = сonst).
Адиабаты (s1, s2, s3) в р-υ-диаграмме – несимметричные гиперболы (рυк = сonst, к =ср / сυ>1), располагаются круче изотерм.
Политропные процессы, описываемые уравнением рυn= сonst, -<n<+, в р-υ- диаграмме – несимметричные гиперболы, в T-s-диаграмме – логарифмические кривые. Направление политропных процессов определяется значением показателя политропы n:
при n = 0 политропный процесс является изобарным;
при n = 1 – изотермическим;
при n = к – адиабатным;
при n = ± - изохорным.
На рис. 1.3 и 1.4 показаны политропные процессы сжатия воздуха с параметрами р1, Т1 до давления р2.

 Рис. 1.3
Рис. 1.4
Рис. 1.3
Рис. 1.4
Обозначения: 1-2Т –
изотермическое сжатие (n=1);
1-2а – адиабатное сжатие (n
= к, для воздуха
![]() );
1-2 - политропное
сжатие (1<n<к);
1-2
- политропное сжатие (n>к).
);
1-2 - политропное
сжатие (1<n<к);
1-2
- политропное сжатие (n>к).
Расчетные формулы для отдельных процессов приведены в табл. 1.1.
Таблица 1.1
Процесс |
Связи параметров |
Работа изменения объема |
Внешняя работа |
Теплота |
Изобарный |
|
|
|
|
Изохорный |
|
|
|
|
Адиабатный |
|
|
|
|
Политроп-ный |
|
|
|
|
В основе получения расчетных формул, приведенных в табл. 1.1, лежат:
уравнение состояния идеального газа
![]() ;
;
математические выражения I и II законов термодинамики
|
(1.9) |
уравнения для работы изменения объема и внешней работы процесса 1-2
|
(1.10) |
Пример расчета процесса идеального газа
Дано: Гелий (![]() )
с параметрами р1 = 20 бар, t1
= 7000C расширяется
в политропном процессе до давления р2
= 5 бар. Показатель политропы n
= 1,73.
)
с параметрами р1 = 20 бар, t1
= 7000C расширяется
в политропном процессе до давления р2
= 5 бар. Показатель политропы n
= 1,73.
Определить работу (![]() )
и теплоту
)
и теплоту
![]() процесса. Представить процесс в р-υ- и
Т-s-диаграммах.
процесса. Представить процесс в р-υ- и
Т-s-диаграммах.
Решение:
Расчетные формулы для политропного процесса даны в табл. 1.1. Температура гелия в конце расширения

Работа изменения объема
![]()
Внешняя работа процесса
![]()
Гелий – одноатомный идеальный газ, для которого теплоемкость и показатель адиабаты – постоянные величины, не зависящие от температуры:
![]()
Теплота политропного процесса
![]()
Построение процесса в диаграммах р-υ и T-s (рис. 1.5 и 1.6) производится по исходным данным. Начальное состояние (точка 1) располагается на пересечении параметров р1 и t1, конечное состояние (точка 2) – на изобаре р2. Направление политропного процесса определяется путем сравнения показателя политропы n = 1,73 с n = 1 (для изотермического процесса) и n=к (для адиабатного процесса).
Так как n>1 и n>к, политропный процесс в р-υ- диаграмме – несимметричная гипербола располагается круче изотермы и адиабаты, в T-s-диаграмме – логарифмическая кривая, пересекающая изобару р2 левее адиабаты.
 Рис. 1.5
Рис. 1.6
Рис. 1.5
Рис. 1.6
Работа (ℓ , ω) и теплота (q) на диаграммах характеризуются заштрихованными площадями. Работа (ℓ , ω) положительна, так как уменьшается давление (р2<р1), увеличивается объем (υ2>υ1). Теплота (q) отводится (отрицательна), так как уменьшается энтропия (s2<s1), что согласуется с результатами расчета.
Тема «Расчет параметров и процессов изменения состояния идеального газа» представлена в [1], с. 185-205.