Лекция 12(28)

5. Рамные системы

5.1. Сдвиговая жесткость многоэтажной рамы

Расчет горизонтальных перемещений, как показали исследования, можно выполнять инженерным методом— допустив равенство углов поворота узлов яруса много­этажной рамы и приняв соответствующую расчетную схему, изображенную на рис. 25,б, в которой s — сумма погонных жесткостей стоек этажа; r — сумма жесткостей ригелей этажа, деленная на усредненный пролет ригелей l_bm (возможна сумма погонных жесткостей ри­гелей этажа); l — длина стойки; п — число этажей.

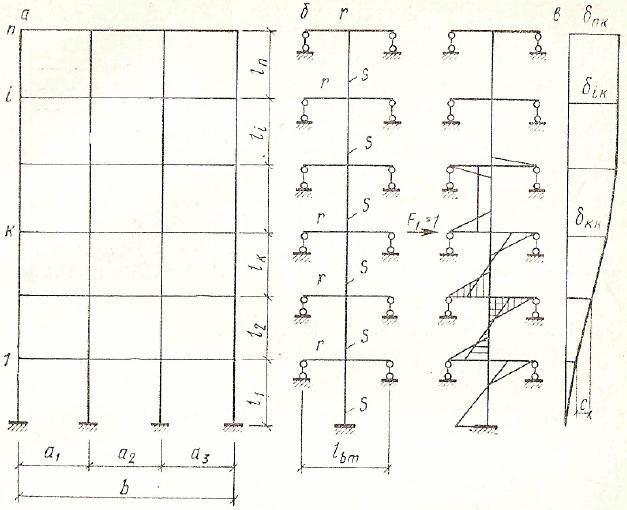
Рис. 25. Расчетные схемы (а, б) и перемещения многоэтажной рамы (в)

Перемещения многоэтажных рам от горизонтальных нагрузок, приложенных одновременно по всем этажам

Перемещения рамы при числе этажей п 6, если принять во внимание, что ярусные поперечные силы

можно определить как сумму поэтажных линейных перекосов (взаимных смещений концов стоек):

(7)

(8)

(9)

где c_i — линейный перекос яруса от единичной силы, приложенной в одном из верхних этажей.

Для многоэтажной рамы регулярной структуры с постоянными по высоте погонными жесткостями s, r и одинаковой высотой этажей l линейный перекос от F=1 можно найти умножением самой на себя эпюры моментов на заштрихованных участках (см. рис. 25, б. Тогда

(10)

После перемножения эпюр получают

(11)

Сдвиговая жесткость многоэтажной рамы — это горизонтальная сила К, при которой угол перекоса равен единице (см. рис. 28, в):

Отсюда (12)

или (13)

При числе этажей п 6 применяют дискретно-континуальный метод, согласно которому сосредоточенная нагрузка заменяется распределенной р(х), сосредоточенные по высоте связи (ригели) — распределенными, а суммирование в (9) — интегрировании. Тогда перемещение

(14)

где Q₀ — поперечная сила от распределенной нагрузки; х — коорди­ната горизонтального сечения рамы.

Последовательным дифференцированием выражения (14) находят:

(15)

(15,а)

Следовательно, при изгибе многоэтажной рамы зависимость между горизонтальным перемещением и поперечной силой выражается первой производной, а кривизна у" с точностью до постоянного множителя К равна внешней нагрузке со знаком минус.

Линия 1 общего изгиба стоек (эпюра смещений ярусов рамы) обращена вогнутостью в сторону начального положения как у системы, работающей на сдвиг, а линия 2 местного изгиба стоек располагается вокруг линии 1, отклоняясь в пределах каждого этажа в ту и другую сторону (рис. 28). В случаях, когда

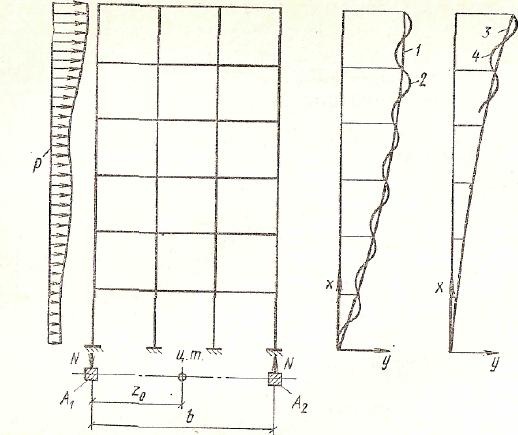
Рис. 28. Перемещения многоэтажной рамы

1 — линия общего изгиба стоек многоэтажной рамы; деформирующейся как сдвиговая система; 2 — линия местного изгиба стоек; 3 — линия общего изгиба стоек с жесткостью, значительно превышающей жесткость ригелей; 4 — то же местного изгиба

стойки обладают жесткостью, значительно превышающей жесткость ригелей, характер их общего изгиба меняется — см. линию 3; при этом поперечная сила — By'", зависящая от суммарной изгибной жесткости стоек , становится весьма существенной. Кроме того, под влиянием деформаций удлинения и укорочения крайних стоек от продольных сил N происходит изгиб рамы как вертикальной консольной конструкции, у которой расстояние между крайними стойками-поясами равно b, а изгибная жесткость — В₀. В средних стойках многопролетной рамы с малоотличающимися пролетами продольные силы незначительны, так как они равны разности поперечных сил ригелей. Дополнительный угол поворота стоек от момента продольной силы в вертикальной конструкции M=Nb в предположении плоского поворота рамы

Тогда выражение поперечной силы при учете деформаций стоек от продольных сил

(16)