
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ (ФИЛИАЛ) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» |
ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ
Курсовая работа
МДК: 04.02 Теоретические основы разработки и моделирования отдельных несложных модулей и мехатронных систем
Тема: Моделирование мехатронной системы
Выполнил
студент группы 7111445
Иванов Иван Иванович
(ФИО)
Проверил
Преподаватель
Галиуллин Ильнар Айратович
(ФИО)
Оценка______________
Дата_________________
Подпись_____________
г. Набережные Челны, 2014г.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ НАБЕРЕЖНОЧЕЛНИНСКИЙ ИНСТИТУТ (ФИЛИАЛ) ФЕДЕРАЛЬНОГО ГОСУДАРСТВЕННОГО АВТОНОМНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» |
ИНЖЕНЕРНО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ
Специальность __220703.51 Автоматизация технологических процессов и производств__
Группа _____7111445 ____
З А Д А Н И Е
на курсовую работу
____________________________Иванов Иван Иванович_____________________________
(фамилия, имя, отчество студента)
МДК 04.02 Теоретические основы разработки и моделирования отдельных несложных модулей и мехатронных систем
Тема Моделирование мехатронной системы
Содержание задания:
Решить задачи моделирования линейной алгебры, произвести моделирование двумерных графиков, моделирование трехмерных графиков, моделирование нелинейной системы, обработать экспериментальные данные и решить задачу оптимизации согласно варианту задания на курсовую работу.
Номер варианта _____1_____
Дата выдачи задания_05.09.2014_
Руководитель _Галиуллин И.А.______________
(подпись, ФИО)
Задание принял к исполнению ______________
(подпись)
Содержание
Введение……………………………………………………………………... |
3 |
1 Моделирование задач линейной алгебры………………………………... |
5 |
2 Моделирование двумерных графиков…………………………………… |
8 |
3 Моделирование трехмерных графиков…………………………………... |
11 |
4 Моделирование нелинейной системы…………………………………… |
16 |
5 Обработка экспериментальных данных…………………………………. |
19 |
6 Оптимизация………………………………………………………………. |
24 |
Заключение…………………………………………………………………... |
25 |
Список использованной литературы………………………………………. |
26 |
Введение
Интенсификация автоматизации производств и инженерных разработок в условиях рыночных отношений, когда реализация новых проектов ведется в жестких временных рамках, обусловила необходимость в программном обеспечении, позволяющем получать результат сложных математических задач моделирования мехатронных систем в приемлемые сроки. В ответ на эту потребность различными фирмами и институтами был создан ряд программных продуктов, к их числу относятся, например, ANSYS, ROOT, MatLab и Scilab. Из числа упомянутых приложений ANSYS и MatLab являются коммерческими, ROOT и Scilab распространяются свободно.
Все приложения этого класса предоставляют пользователю командный интерфейс, с помощью которого производится описание математической формулировки задачи. После выполнения каждой команды можно видеть результат ее выполнения. Последовательным выполнением команд, по существу, создается программа, которая состоит из обращений к соответствующим высокоуровневым функциям, предоставляемым системой. Например, чтобы нарисовать график зависимости f(x), необходимо вызвать функцию рисования графиков, сообщить этой функции вид f(x)и, возможно, ее область определения. Каждая из систем использует собственный язык программирования высокого уровня, за исключением ROOT, где применяется C++.
Языки программирования каждой из упомянутых систем несовместимы между собой, однако программы, написанные на языке MathLab, могут быть импортированы в Scilab с помощью встроенных средств системы. Обстоятельством, которое препятствует использованию этих систем в России, является отсутствие русскоязычного интерфейса и документации на русском языке.
Система Scilab оснащена обширным встроенным справочником, однако информация в нем доступна лишь на английском и французском языках.
Scilab – это система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений, таких как:
решение нелинейных уравнений и систем;
решение задач линейной алгебры;
решение задач оптимизации;
дифференцирование и интегрирование;
обработка экспериментальных данных (интерполяция и аппроксимация, метод наименьших квадратов);
решение обыкновенных дифференциальных уравнений и систем.
Кроме того, Scilab предоставляет широкие возможности по созданию и редактированию различных видов графиков и поверхностей.
Несмотря на то, что система Scilab содержит достаточное количество встроенных команд, операторов и функций, отличительная ее черта – это гибкость. Пользователь может создать любую новую команду или функцию, а затем использовать ее наравне со встроенными. К тому же, система имеет достаточно мощный собственный язык программирования высокого уровня, что говорит о возможности решения задач моделирования мехатронных систем.
1 Моделирование задач линейной алгебры
1.1 Решить систему линейных алгебраических уравнений, сделать проверку:
 .
.
Решение:
-->//Свободные коэффициенты вводятся как вектор- столбец и с учетом знаков. Матрица коэффициентов:
-->A=[2 1 5 1;0.333 -1 0 -2;0 2 1 2;1 4 7 6];
-->b=[8;3;-5;0]; //Вектор свободных коэффициентов
-->A1=A;A1(:,1)=b; //Первая вспомогательная матрица
-->A2=A;A2(:,2)=b; //Вторая вспомогательная матрица
-->A3=A;A3(:,3)=b; //Третья вспомогательная матрица
-->A4=A;A4(:,4)=b; //Четвертая вспомогательная матрица
-->D=det(A); //Главный определитель
-->//Определители вспомогательных матриц:
-->d(1)=det(A1);
-->d(2)=det(A2);
-->d(3)=det(A3);
-->d(4)=det(A4);
-->x=d/D //Вектор неизвестных
-->x=
2.9980013
- 3.9992227
1.0008883
0.9987786
-->D=A*x-b //Проверка
D =10^(-14) *
0.1776357
0.0888178
- 0.1776357
- 0.0888178
1.2 Если можно, вычислить матрицу, обратную к матрице D.
![]() ,
где
,
где ![]()
Решение:
//Ввод элементов матрицы осуществляется в квадратных скобках, при этом элементы строки отделяются друг от друга пробелом или запятой, а строки разделяются между собой точкой с запятой:
-->A=[7 2 0;-7 -2 1;1 1 1];
-->B=[0 2 3;1 0 -2;3 1 1];
-->//Вычислить
-->D=(A^2-B^2)*(A+B^2)
D =
356. 130. 17
- 397. - 138. - 8
- 6. - 51. – 63
//inv(D) – вычисляет матрицу, обратную к матрице D
-->inv(D)
ans =
0.2384529 0.2107399 0.0375838
- 0.7183804 - 0.6424933 - 0.1122622
0.5588362 0.5000432 0.0714265
2 Моделирование двумерных графиков
2.1
Изобразите график функции f(x).
![]()
Решение:
Рассмотрение графиков начнем с простейших функций вида y = f (x), для построения которых в Scilab существует функция plot. В предыдущих версиях Scilab (по третью версию Scilab включительно) функция plot предназначена для построения графика одной функции y = f (x). Обращение к ней имеет вид:
plot(x,y,[xcap,ycap,caption])
Здесь x — массив абсцисс; y — массив ординат; xcap, ycap, caption — подписи осей X, Y и графика соответственно.
Пусть x изменяется на интервале [−1.5; 1.5] с шагом 0,1. Сформируем массив X. Вычисляя значение функции для каждого значения массива X, создадим массив Y . Затем воспользуемся функцией plot(x,y) для построения кривой.
Установить желаемый вид и цвет графика можно, используя полную форму обращения к функции plot:
plot(x1, y1, s1, x2, y2, s2, ..., xn, yn, sn)
где x1, x2, ..., xn — массивы абсцисс графиков;
y1, y2, ..., yn — массивы ординат графиков;
s1, s2, ..., sn — строка, состоящая из трех символов, которые определяют со-ответственно цвет линии, тип маркера и тип линии графиков, в строке могут использоваться один, два или три символа одновременно в любой желаемой комбинации.
Пусть наш график функции будет синего цвета, с маркером в виде звездочки,
-->x=-1.5:0.1:1.5;
-->f= (((x-4.5).^2).*(x+2)).^1/3;
-->plot (x, f, 'm' ,'p')
-->xgrid()
Чтобы график проще «читался», удобно выводить сетку — дополнительные оси для показателя X и показателя Y . В Scilab это можно сделать с помощью команды xgrid(color), где color определяет цвета линии сетки. Если оставить скобки пустыми, по умолчанию будет прорисована сетка черного цвета.
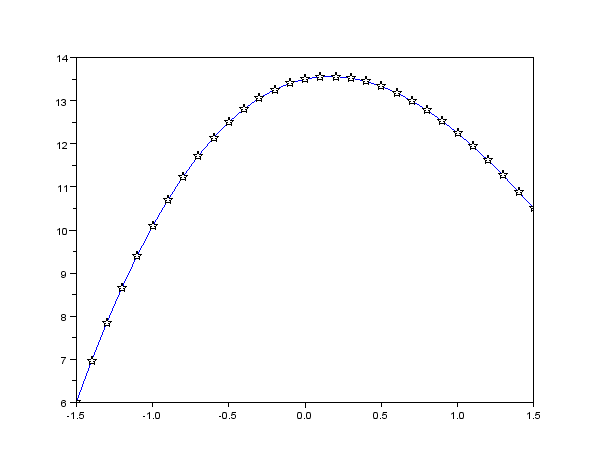
Рисунок 2.1 График без команды xgrid()
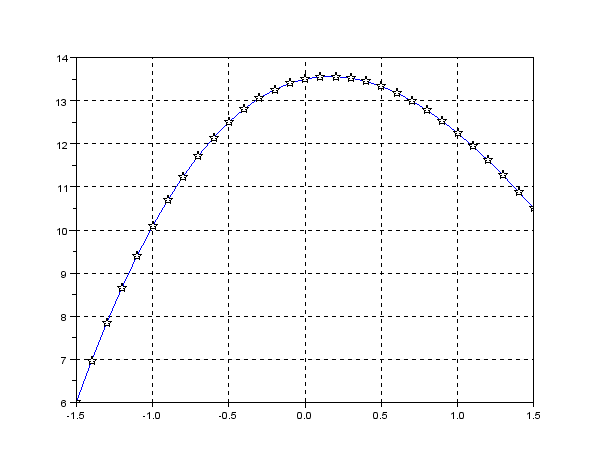
Рисунок 2.2 Применение команды xgrid()
2.2
Изобразите график функции в полярных
координатах. ![]() .
.
Решение:
Полярная система координат состоит из заданной фиксированной точки O – полюса, концентрических окружностей с центром в полюсе и лучей, выходящих из точки O, один из которых OX — полярная ось.
В Scilab для формирования графика в полярной системе координат необходимо сформировать массивы значений полярного угла и полярного радиуса, а затем обратиться к функции polarplot:
polarplot(fi,ro,[key1=value1,key2=value2,...,keyn=valuen]),
где fi — полярный угол;
ro — полярный радиус;
keyn=valuen — последовательность значений свойств графика.
Определив диапазон и шаг изменения полярного угла, формируем массивы fi, ro. Cтроим кривую с помощью функции polarplot, при этом для линии графика функции ro установим красный цвет.
-->fi=0:0.01:2*%pi;
-->ro=2*sin(6*fi);
--> polarplot (fi, ro, style=color("red"));
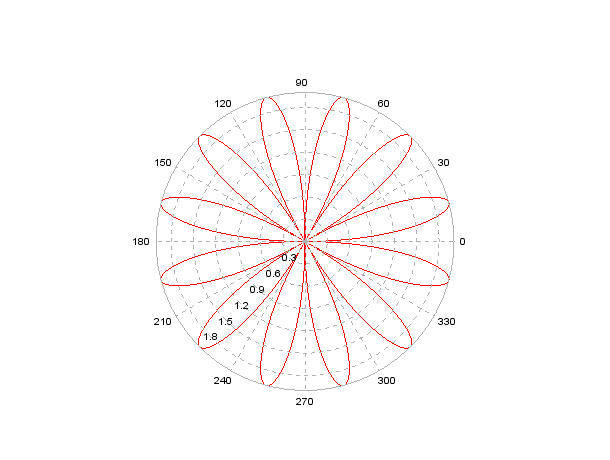
Рисунок 2.3 График функции в полярных координатах
