Глава 4. Канонические разложения случайных процессов
4.1. Понятие канонического разложения случайного процесса
Случайная величина V называется центрированной, если ее математическое ожидание равно 0. Элементарным центрированным случайным процессом называется произведение центрированной случайной величины V на неслучайную функцию φ(t): X(t)=V φ(t). Элементарный центрированный случайный процесс имеет следующие характеристики:
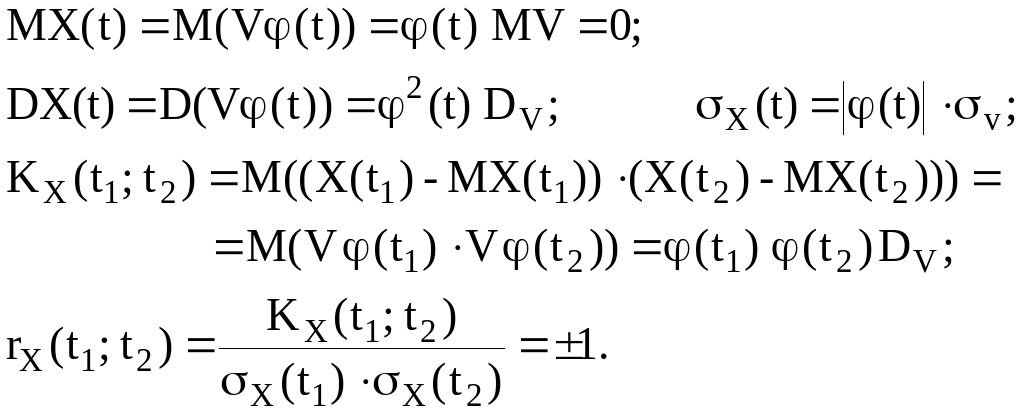
Выражение вида
,
где φk(t),
k=1;2;…-неслучайные
функции;
,
k=1;2;…-некоррелированные
центрированные случайные величины,
называется каноническим разложением
случайного процесса X(t),
при этом случайные величины
называются коэффициентами канонического
разложения; а неслучайные функции
φk(t)
-
координатными функциями
канонического разложения.
Рассмотрим характеристики случайного процесса
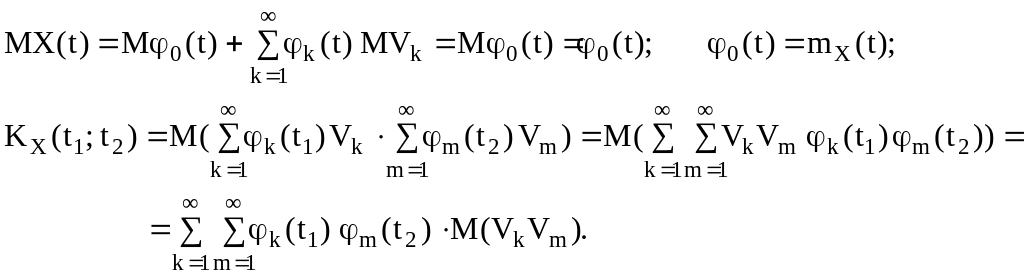
Так как по условию
то
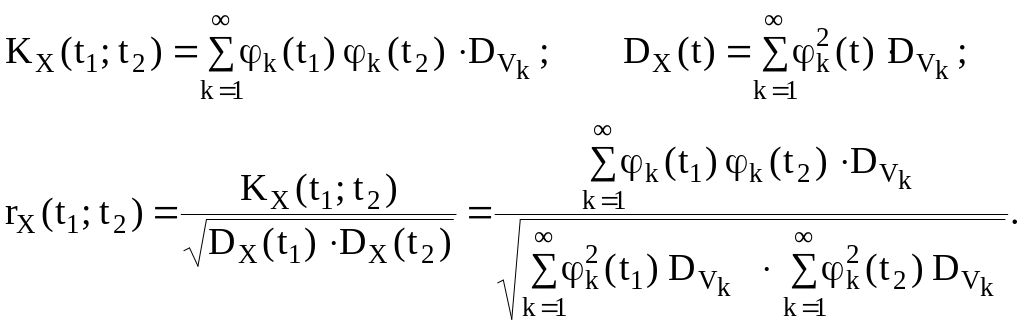
Очевидно, что один
и тот же случайный процесс имеет
различные виды канонического разложения
в зависимости от выбора координатных
функций. Более того, даже при состоявшемся
выборе координатных функций существует
произвол в распределении случайных
величин Vк.
На практике по итогам экспериментов
получают оценки для математического
ожидания и корреляционной функции:
.
После разложения
в
двойной ряд Фурье по координатным
функциям φк(t):
получают
значения дисперсий
случайных
величин Vk.
Пример 7.
Случайный процесс Х(t)
имеет следующее каноническое разложение:
,
где Vk-нормально
распределенные некоррелированные
случайные величины с параметрами (0;
σк);
m0(t)
- неслучайная функция. Найти основные
характеристики случайного процесса
Х(t),
включая плотности распределения.
Решение.
Из полученных ранее общих формул имеем:
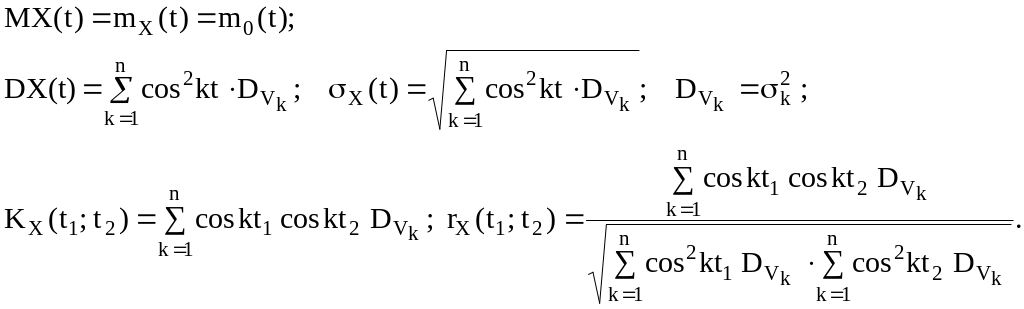
В каждом сечении случайный процесс Х(t) имеет нормальное распределение, так как является линейной комбинацией некоррелированных нормально распределенных случайных величин Vk, при этом одномерная плотность распределения имеет вид:
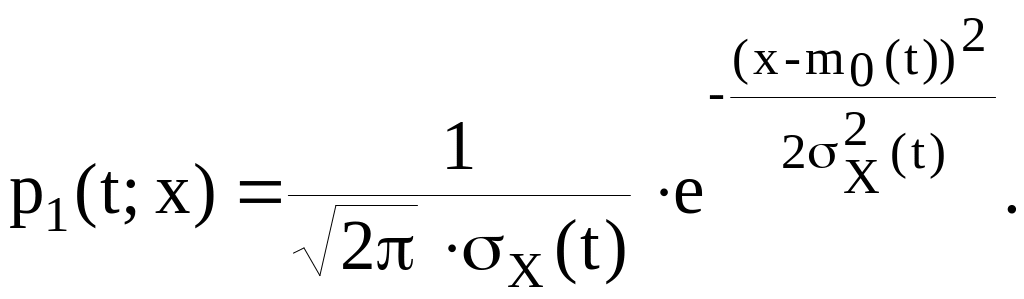
Двумерный закон распределения также является нормальным и имеет следующую двумерную плотность распределения:
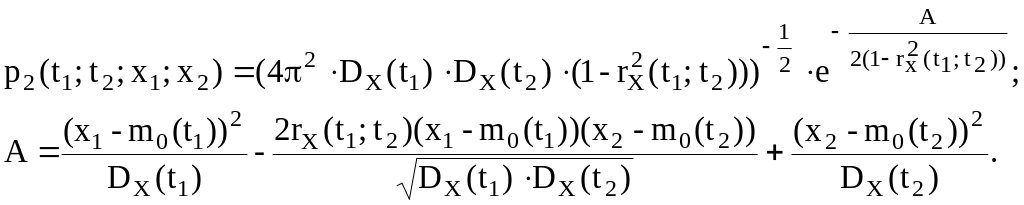
Пример 8.
Известны
математическое ожидание mX(t)
и корреляционная функция КX(t1;t2)=t1t2
случайного
процесса Х(t),
где
.
Найти каноническое разложение Х(t)
по координатным функциям
при условии, что коэффициенты разложения
Vk
- нормально
распределенные случайные величины.
Решение.
Корреляционная функция имеет следующее разложение
,
следовательно,
;
;
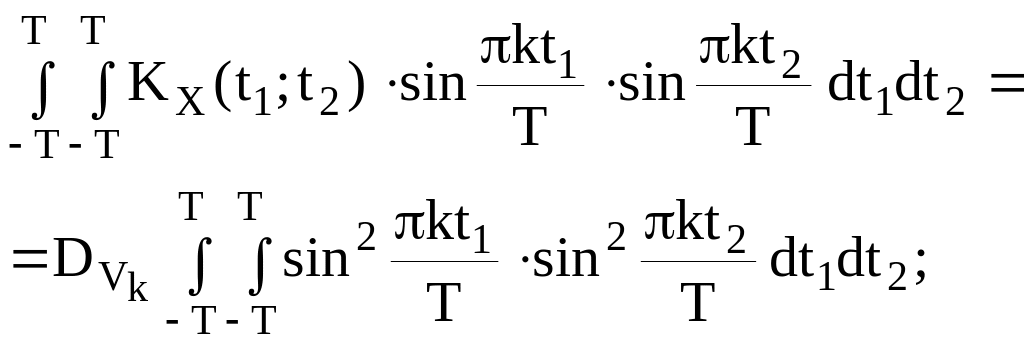
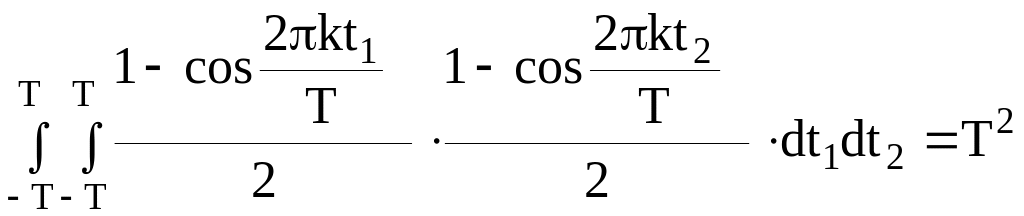Так как
,
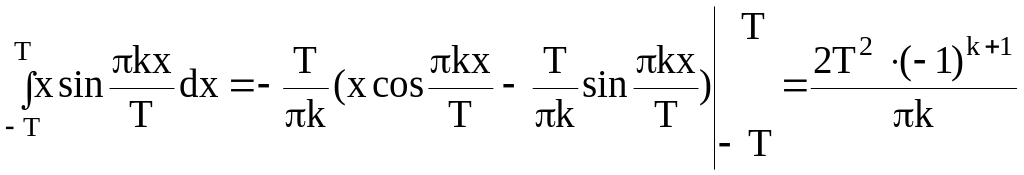то
;
.
Плотность распределения случайных величин Vk:
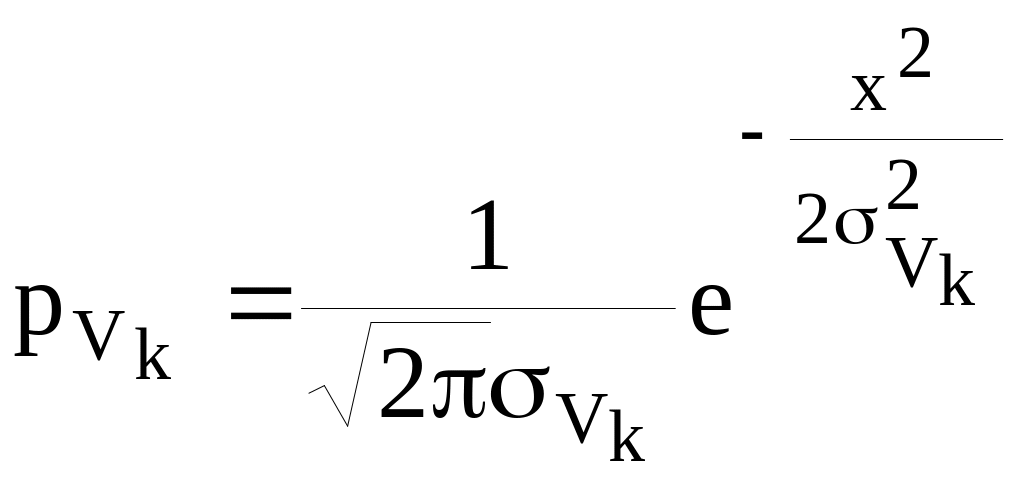
Каноническое разложение случайного процесса Х(t) имеет вид:
.
4.2. Понятие обобщенной функции. Дельта-функция Дирака.
Интегральное каноническое представление случайных процессов.
Обобщенной функцией называется предел последовательности однопараметрического семейства непрерывных функций.
Дельта-функция
Дирака
-
это обобщенная функция, являющаяся
результатом предельного перехода при
в семействе функций
Среди
свойств
-функции
отметим следующее:
1.
2.
3. Если f(t)- непрерывная функция, то
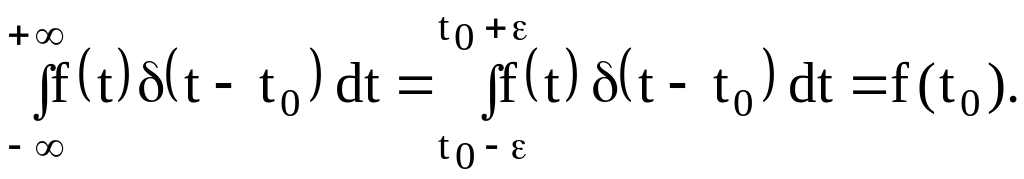
Случайный процесс Х(t), корреляционная функция которого имеет вид
называется нестационарным «белым шумом». Если W(t1)=W - const, то Х(t)-стационарный «белый шум».
Как следует из определения, никакие два, даже сколь угодные близкие, сечения «белого шума» не коррелированны. Выражение W(t) называется интенсивностью «белого шума».
Интегральным каноническим представлением случайного процесса Х(t) называется выражение вида
где
- случайная центрированная функция;
-
неслучайная функция непрерывных
аргументов
Корреляционная функция такого случайного процесса имеет вид:
.
Можно показать, что существует неслучайная функция G(λ) такая, что
где G(λ1)
- плотность дисперсии; δ(х) - дельта-функция
Дирака. Получаем
Следовательно, дисперсия случайного процесса Х(t):
.