2.2. Математическое ожидание и дисперсия случайного процесса.

Среднеквадратическое отклонение

Если в каждом сечении случайного процесса существует математическое ожидание, то математическим ожиданием случайного процесса X(t) называется неслучайная функция m_X(t), значение которой при каждом фиксированном значении t равно математическому ожиданию соответствующего сечения:

m_X(t)=MX(t).

Основные свойства математического ожидания случайного процесса: если φ(t) - неслучайная функция, то

М φ(t)=φ(t); М(φ(t)X(t))=φ(t)m_X(t);

M(X₁(t)+X₂(t))= ; M(X(t)+φ( t))= m_X(t)+ φ(t).

Если в каждом сечении случайного процесса существует дисперсия, то дисперсией случайного процесса X(t) называется неслучайная функция D_Х(t), значение которой при каждом фиксированном значении аргумента t равно дисперсии соответствующего сечения:

D_X(t)= DХ(t)= M(X(t)-m_X( t))².

Основные свойства дисперсии случайного процесса:

если φ(t) - неслучайная функция, то

D(φ(t))=0; D(φ(t)X(t))=φ²(t)D_X(t);

D(X(t)+φ(t))=D_X(t); .

Среднеквадратическим отклонением случайного процесса X(t) называется арифметический квадратный корень из его дисперсии:

.

2.3. Корреляционная функция случайного процесса и ее свойства.

Нормированная корреляционная функция

Корреляционной функцией случайного процесса X(t) называется неслучайная функция K_X(t₁; t₂) двух независимых аргументов, значение которой равно корреляционному моменту сечений, соответствующих моментам времени t₁ и t₂:

K_X(t₁; t₂)=M((X(t₁)-m_X(t₁))(X(t₂)-m_X(t₂))).

Основные свойства корреляционной функции:

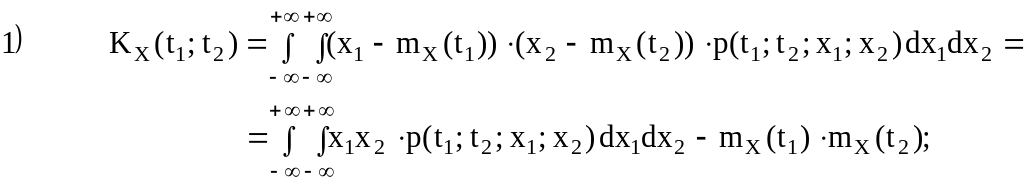
2) K_X(t; t)=D_X(t);

3) K_X(t₁; t₂)= K_X(t₂; t₁);

4) если φ(t) - неслучайная функция, то

K_φ(t)(t₁; t₂)=0; K_φ(t)+X(t)(t₁; t₂)= K_X(t)(t₁; t₂);

K_φ(t)X(t)(t₁; t₂)= φ(t₁) φ(t₂)K_X(t)(t₁; t₂);

5)

6)

Функция вида

называется нормированной корреляционной функцией.

2.4. Взаимная корреляционная функция и нормированная взаимная

корреляционная функция двух случайных процессов

Взаимной корреляционной функцией двух случайных процессов X(t) и Y(t) называют неслучайную функцию R_XY(t₁; t₂) двух независимых аргументов t₁ и t₂, значение которой равно корреляционному моменту сечений этих случайных процессов в соответствующие моменты времени:

R_XY(t₁; t₂)= M((X(t₁)-m_X(t₁))(Y(t₂)-m_Y(t₂))).

Свойства взаимной корреляционной функции:

если φ(t) и Ψ(t) - неслучайные функции, то

R_{X(t)+φ(t) Y(t)+Ψ(t)}(t₁; t₂)= R_XY(t₁; t₂);

R_{X(t)φ(t) Y(t)Ψ(t)}(t₁; t₂)= φ(t₁) Ψ(t₂)R_XY(t₁; t₂);

R_XY(t₁; t₂)=R_YX(t₂; t₁);

Функция вида

называется нормированной взаимной корреляционной функцией случайных процессов X(t) и Y(t).