3.15.2 Расчет простого трубопровода

Одна из задач расчёта трубопровода – определить минимальную мощность, необходимую для доставки данного количества жидкости в заданную точку, т.е. на определённое расстояние.

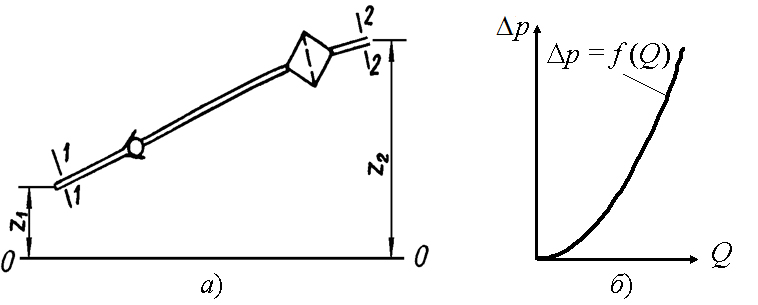
Рисунок 3.32 - Простой трубопровод (а) и характеристика простого

трубопровода(б)

Пусть простой трубопровод (рисунок 3.32, а) постоянного сечения расположен произвольно в пространстве, имеет общую длину l и диаметр d и содержит ряд местных сопротивлений. В начальном сечении (1-1) имеем нивелирную высоту z₁ и избыточное давление р₁, а в конечном (2-2) – соответственно z₂ и р_2. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна .

Запишем уравнение Бернулли сечений 1-1 и 2-2

;

где – сумма потерь полного напора на участке между сечениями;

υ_ср – средняя величина скорость по сечению;

 – коэффициент Кориолиса, учитывающий неравномерность распределения скорость по сечению потока.

Суммарные потери на трение по длине и на местных сопротивлениях на участке трубы длиной l. Потери будут определяться по формулам

и .

Учитывая уравнение неразрывности потока и постоянство диаметра трубы т. е. и , скоростные напоры в обеих частях можно сократить. Тогда уравнение Бернулли примет вид

(1)

Выразив величину скорости через расход и подставив в выражение (1) получим формулу

или (2)

где - гидравлическое сопротивление трубопровода.

Выражение (2) называется характеристикой трубопровода при турбулентном движении жидкости. Эта характеристика представляет собой зависимость суммарных потерь давления (напора) от расхода в трубопроводе ( ) (рисунок 3.32, б).

Если в трубопроводе установлены гидравлические аппараты, имеющие свои сопротивления, то их необходимо добавить к коэффициенту сопротивления трубопровода, и в результате получится суммарное гидравлическое сопротивления.

3.15.3 Последовательное соединение трубопроводов

Последовательный трубопровод состоит из нескольких труб различной длины и различного диаметра, соединённых между собой (рисунок 3.33, а).

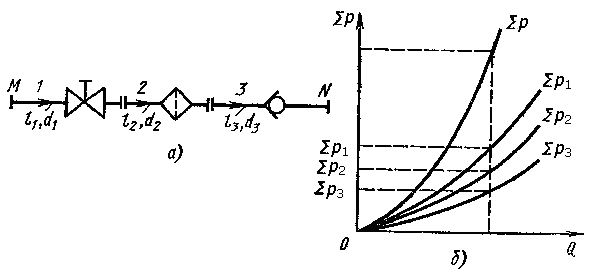
Рисунок 3.33 – Последовательное соединение трубопроводов (а)

и построение суммарной характеристики трубопроводов (б)

В каждом из этих трубопроводов могут иметься свои местные сопротивления. Течение в жидкости в такой трубе подчиняется следующим условиям:

• расход на всех участках трубопровода одинаков, т.е. Q₁ = Q₂ = Q₃;

• потери давления (напора) во всём трубопроводе равны сумме потерь на каждом участке :

.

С учётом сказанного нетрудно получить уравнение для определения суммарных потерь давления, которое примет вид

, , (3)

где , , - гидравлическое сопротивление соответственно первого, второго, и третьего участков трубопровода;

- суммарное гидравлическое сопротивление всего трубопровода.

Величина суммарного сопротивления с учётом ранее полученной формулы для простых трубопроводов составит

;

.

В общем случае выражение, описывающее суммарное гидравлическое сопротивление сложного трубопровода, будет выглядеть

.

Уравнение, определяющее суммарные потери давления, представляет собой характеристику сложного трубопровода, которая является суммой характеристик простых трубопроводов. Это уравнение позволяет узнать, какие энергетические характеристики должен иметь источник энергии, чтобы жидкость могла протекать по всему трубопроводу. Однако в конечной точке этой трубы энергия жидкости будет равна нулю. Если в конце трубы необходимо иметь какое-то давление p_нагр (например, чтобы преодолевать нагрузку) к величине нужно добавить эту величину. Кроме того, т.к. в общем случае величина скоростного напора в начале и в конце трубопровода из-за разных диаметров различны, необходимо добавить и эту разницу к . В результате энергия, которой должен обладать источник, должна составлять

.

Если переписать это уравнение, заменив скорость жидкости отношением расхода к площади живого сечения, получим

или или

где - коэффициент.

Сумма в этом выражении – общее гидравлическое сопротивление сложного трубопровода.

Из приведённых уравнений вытекает следующее важное правило: для построения характеристик последовательного соединения нескольких трубопроводов следует сложить ординаты (потери давления) характеристик каждого из этих трубопроводов при одинаковых абсциссах (расходах) (рисунок 3.33, б).