11.1. Число Рейнольдса. Характеристика режимов течения вязкой жидкости.
Характеризует режим движения вязкой жидкости в трубах и руслах.
Связь сил инерции и сил вязкости при изучении подобных течений на модели и в натуре выражается числом Рейнольдса.
Число Рейнольдса есть отношение сил инерции к силам вязкости в потоках реальной жидкости.
Если число Рейнольдса мало, то в потоке преобладают силы вязкости, если велико – силы инерции.
50.
http://vunivere.ru/work12542 - только ссылка, текст не копируется
Н еравномерное движение грунтовых вод
Все вопросы равномерного движения грунтовых вод решаются на основе уравнения Дарси Q= kфωЈ, а для плоской задачи при q = Q/B = kфhoЈ. Тогда глубина фильтрационного потока ho= q/kфЈ или ho= q/kфі, где і- уклон водоупора. В основу исследования неравномерного движения положена формула Дюпюи. Так выбрав сечение n- n (рис. 7.4) при неравномерном движении потока, напишем для него уравнение Бернулли H = z + p/γ + αυ2/2ġ. Учитывая, что p/γ =h и равна глубине потока, а величина αυ2/2ġ бесконечно мала и ей можно пренебречь, тогда H = z + h. Продифференцировав это уравнение и разделив на –dS, получим –dH/dS =-dZ/dS – dh/dS, где -dH/dS = J- уклон свободной поверхности, а -dZ/dS = i – уклон дна. Подставив это уравнение в уравнение расхода Q = kфω(і - dh/dS) или для погонного расхода q = kфh(і - dh/dS) основное уравнение движения грунтовых вод(первая форма). Для равномерного движения грунтовых вод это уравнение выглядит q = kфho і, где ho- глубина равномерного режима движения фильтрационного потока, но так как ho і = h(і - dh/dS), тогда kфho і = kф h(і - dh/dS), разделив на kф получим уравнение во второй форме dh/dS = і (h – ho)/h.
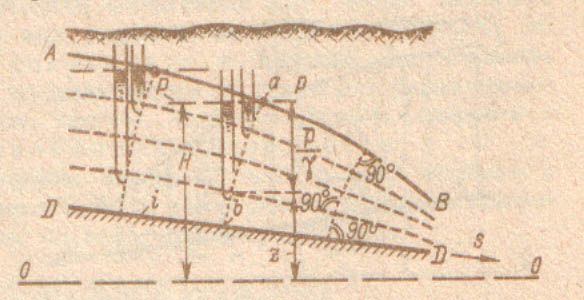
Рис. 7.4. Схема действующего фильтрационного потока
в случае плавно изменяющего движения
Анализируя полученное уравнение при уклоне дна (водоупора) і > 0 и h > ho получим dh/dS>0 т.е. кривую подпора. При h < ho получаем dh/dS < 0, т.е. кривую спада.
При і = 0 анализируя уравнение первой формыq = -kфh dh/dS выражение dh/dS должно быть всегда отрицательным (dh/dS < 0) т.к. расход q есть величина положительная. Значит, во всех случаях имеется только кривая спада.
Безнапорное движение грунтовых вод
Водопроницаемый грунт состоит из отдельных частиц (песчинок) между которыми имеются поры, составляющие от 30 до 45 % от объема всего грунта. Явление движения воды в этих порах называется фильтрацией. Вода в поры может попасть различным способом. Например, инфильтруя в грунт после дождя и задерживаются пластом водонепроницаемого грунта (глиной, скалой) и будет двигаться в направлении его уклона (рис. 7.1). Водонепроницаемый слой (водоупор) образует как бы русло грунтовой воды со свободной поверхностью. Такие потоки называются безнапорными и являются в основном ламинарным, кроме движения фильтрационного потока в крупнозернистых грунтах (гравий, галька или трещиноватая скала), где движение потока является турбулентным.
Рис. 7.1. Фильтрационный поток (поток грунтовой воды)
Движение грунтовых вод может быть равномерным и неравномерным, напорным и безнапорным. Напорный поток может существовать только при существовании водоупоров снизу и сверху фильтрационного потока, давление в котором определяется источниками водозабора. Свободная поверхность фильтрационного потока называется депрессионной поверхностью или для плоской задачи- кривой депрессии. Задача расчета фильтрационного потока заключается в определении положения кривой депрессии и установлении фильтрационного расхода. На рис. 7.2 а представлен случай фильтрации воды из канала в реку; с тем, чтобы оценить величину потерь воды из канала на фильтрацию по формуле Q = vω, где v- фиктивная скорость фильтрации, а ω – площадь живого сечения грунтового потока. На рис. 7.2 б представлена система дрен, в которую поступает грунтовая вода и для построения кривой депрессии необходимо установить фильтрационный расход. На рис. 7.2 в показано положение кривой депрессии в земляной плотине.
а)
Рис. 7.2. а. Фильтрация воды из канала в реку.
б)
Рис. 7.2. б. Система дрен, в которые поступает грунтовая вода
б)
Рис. 7.2 в. Земляная плотина, через которую просачивается вода