§ 81. Уравнивание систем съемочных ходов с одной узловой точкой способом среднего весового

⁽³²⁶⁾

Раздел IV. Ушшше гецезиейи сетей сгущеяя1 и съемичных сетей

Способ среднего весового применяют для уравнивания небольших несвободных систем нивелирных, теодолитных или тахеометрических ходов.

ПШ 14. УМЦЕН1ВЕ Ш1ИИВАИЕ СЪЕМОТЁЫК СЕТЕЙ

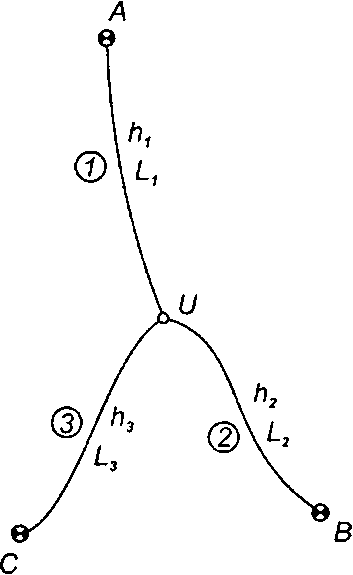
Система нивелирных ходов с одной узловой точкой. От исходных реперов А, В, С с отметками Н_А, Н_в, Н_с проложены нивелирные ходы, сходящиеся в узловой точке V (рис. 93). Измерены длины ходов I., число станций в ходе л. и превышения по каждому ходу (1, 2, 3).

весового

ки Н_ь, узловой точки по формуле среднего

вычисляют значение отмет­

дому ходу А

Н₃ = Н_с+к₃

Приняв веса суммы превышений по каж-

и

(333)

(332)

(331)

Находят отметку узловой точки Ц по каждому ходу:

_Р,Н,+р₂Н₂+р₃Н₃ _[рН]

Пу — — г _П ,

или

Р\+ Р 2+ Рз [р\

И -И ЛеА [рУ

где Н - приближенное значение высоты _{?ис дз Система нцв} узловой точки; е_гн_{ -н₀ — остатки. ^ _{с одной ой}

В результате систему ходов с одной уз- точкой

(334)

ловой точкой (см. рис. 93) можно рассматри­вать как систему одиночных нивелирных ходов с высотой конечной точки равной Н_ц. Невязки в сумме превышений по каждому ходу нахо­дят из выражений

Щ = Н_и-Н₁₉ К₂ = Н_и-Н₂,

к₃ = н_и-н₃

Далее вычисляют поправки в каждое превышение /-го хода (/ = 1, 2, 3) по формуле (328) для всхолмленных или по формуле (330) — для равнин­ных районов.

Характеристикой точности измерений является, как известно, сред­няя квадратическая погрешность единицы веса //.

Учитывая, что при определении веса суммы превышений по каждо­му ходу величина I. выражается в километрах, можно записать

(335)

где т_ш — средняя квадратическая погрешность в превышении ниве­лирного хода длиной 1 км («километрическая погрешность»); и= — ИЛ; N — число ходов (в рассматриваемом случае N = 3).

Раздел IV. Уршише гецезиесш сете! сгсцеш I съемниых сете!

Средняя квадратическая погрешность высоты узловой точки Н_у определится по формуле

¹³³⁶¹

Если вес суммы превышений хода вычисляется с учетом числа стан- _ 1

ций как то из выражения (335) находят среднюю квадратиче­

скую погрешность превышения, измеренного на станции, т. е.

= (337)

Пример уравнивания системы нивелирных ходов, показанной на рис. 93, приведен в табл. 31.

Таблица 31

Уравнивание системы нивелирных ходов с одной узловой точкой Н_А = 120,157 м, Н_в = 130,412 м, Н_с = 111,310 м

№ хода	А„ м	Нь м	А» м	А	€ у ММ	ре, мм	г/,, мм	р1?> мм	рV2	руе
1	+1,085	121,242	8,2	0,12	39	4,7	-17	-2,0	34	-78
2	-9,209	,203	7,1	0,14	0	0,0	+22	+3,1	68	0
3	+9,920	,230	6,0	0,17	27	4,6	-5	-0,8	4	-22

121,203 м [р] = 0,43 [ре] = 9,3 [ри] = + 0,3 [рш]=-№ ^ = 21,60 мм [ри²]= 106

^ни = ^но = 121.203+0,022 = 121,225 м;

И

/Г^Й [Ж А 7,5

Система теодолитных ходов с одной узловой точкой. Известны плановые координаты исходных пунктов В, К, Р (рис. 94) и дирекцион­ные углы исходных линий Одд, а_сю а_ЕР. Измерены горизонтальные углы /}. и длины линий й..

При упрощенном уравнивании системы теодолитных ходов с одной узловой точкой по общепринятой схеме сначала уравнивают углы по способу среднего взвешенного. Вычислив по уравненным углам дирек­ционные углы и приращения координат, производят раздельное урав­нивание приращений координат Ах и Ау по каждому ходу.

Для уравнивания углов выбирают узловую линию, в качестве кото­рой может быть принята любая линия, опирающуюся на узловую точ­ку (в нашем примере линия 110).

Вычисляют значения дирекционного угла узловой линии по каждо­му ходу:

(338)

где п. — число углов до узловой линии в /-м ходе (/ = 1, 2, 3); \/?\ — сумма углов в /-м ходе.

_ 1

п1м и. ямщеше ун11ише сю1инд спй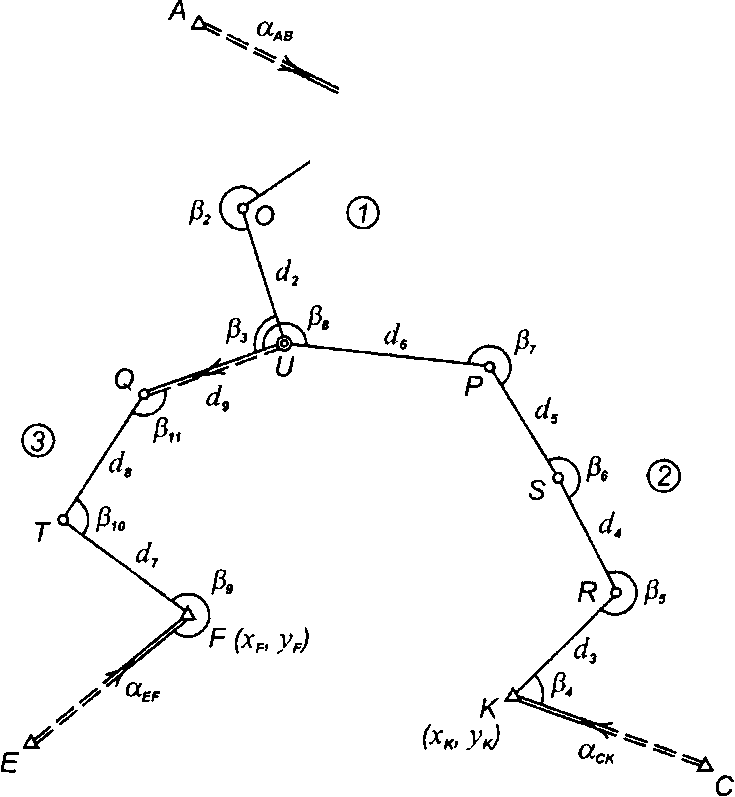

в (х_а, у в)

ч

Рис. 94. Система теодолитных ходов с одной узловой точкой

Приняв вес суммы углов /-го хода равным Л окончательное зна-

(339)

чение дирекционного утла узловой линии вычисляют по формуле сред­него взвешенного

_ Р,<*'цд + Р₂^аид + Рз^цд Р1+Р2+Р3

Как и при уравнивании системы нивелирных ходов, находят угло­вые невязки Щр по каждому ходу:

к	= аид
	= аив
цг;

Распределив угловые невязки поровну на углы соответствующего хода с противоположным знаком, находят уравненные значения углов. По уравненным углам вычисляют приращения координат по всем ли­ниям ходов и находят суммы приращений координат по каждому ходу

[Дх]. и [Ду].. Уравнивание приращений координат производят раздельно

(341)

для Дх и Ау аналогично уравниванию превышений системы нивелир­ных ходов с одной узловой точкой по формулам:

х'_и =х_в+[Ах]_г' ^хи =х_к+[Ьх]₂;

(342)

х"=хг+[&х]₃

_х ^ Р1^х'ц + Р2^хи + Р)Хц ^и Р1+Р2+Р)

1

где р. — вес абсциссы (ординаты) узловой точки; [ь\ —длина /-го хода. Вычисляют невязки в приращениях координат по каждому ходу

(343)

Щ'=^хи-^Хи>*

Щ=^хи~^хи

Поправки в приращения координат находят по формуле, аналогич­ной (328), т. е.

(344)

[4

где

;-я длина стороны /-го хода. Для уравнивания приращений ординат используют выражения (341) — (344), заменив х на у (см. табл. 32).

тт к. ттш гедиезиесш сете! спцеии и съемотмых сете!

(340)

По исправленным приращениям координат вычисляют координаты всех пунктов сети.

- М

Оценку точности измерения углов производят по известной из тео­рии погрешностей формуле, которая в данном случае дает приближен­ное значение средней квадратической погрешности измерения утла

где N — число ходов.

ГНШ 14 тщт Ш18Ш ЕШШ СЕТЕ!

Таблица 32

Уравнивание системы теодолитных ходов с одной узловой точкой

Пункты	Измеренные углы, р.	Дирекцион­ные углы,	Длины сторон, Ьььл	Приращения координат, м		Координаты, м
				Ах	Ау	X	У
1-й ход
А
		54° 10,3'
В	-3 185°48,0'					5548,34	2380,98
		48°22,6'	304,53	-19 +202,28	+19 +227,65
О	179°49,0'					5750,43	2608,82
		48°33,9'	304,76	-19 +201,98	+18 +228,48
V	-2 128°00,9'					5951,92	2837,48
		100°33,2'
Я
[/]=	493°37,9' 493°37,Г +0,8'	1*1 =	609,29	+403,96 +403,58 ЦГх =+0,38	+456,13 +456,50 ЦТ =-0,37
						IVь = ^ + IV; =0,44 м IV 7 1 1150
2-й ход
С
		137°07,3'
К	198°35,2'					6958,85	2136,41
		118°32,Г	318,32	+6 -152,06	-1 +279,65
я	142°00,6'					6806,85	2416,05
		156°31,5'	267,40	+5 -245,27	+106,52
	184°49,3'					6561,63	2522,57
		15! °42,1'	353,24	+7 -311,02	-1 +167,46
Р	+1 177°58,0'					6250,68	2690,02
		153°44,0'	333,23	+6 -298,82	-1 +147,47
V	+/ 233°10,7'					5951,92	2837,48
		100°33,2'
Я
	36°33,8' 936°34,Г -0,3'	12 =	1272,19	-1007,17 -1006,93 \УХ =-0,24	+701,10 +701,07 IV =+0,03
						IV 1 от" 1 5300
3-й ход
Е
		328°25,3'
Г	+2 201 °51,6'					5512,83	3408,06
		306°33,5'	196,34	+9 +116,95	-12 -157,71
Т	+.2 167°36,5'					5629,87	3250,23
				+17	23

№Щ IV. УШШШ1Е ГЕЦЕЗИЕСШ СЕТЕЙ СГУЩЕНШ И ШШ СЕТЕ!

Окончание табл. 32

Пункты	Измеренные углы, Д	Дирекцион­ные углы, а.	Длины сторон, и м	Приращения координат, м		Координаты, м
				Ах	■Ау	X	У
я	+2 218°24,4'					5922,46	2995,32
		280°33,2'	160,46	+7 +29,39	-9 -157,75
V						5951,92	2837,48
и II II	587°51,5' 587°52,Г -0,6'		744,58	+438,76 +439,09 ЦГХ =-0,33	-570,14 -570,58 IV =+0,44	+№у2 =0,55 м IV Льш-1- от" Ь 1350

Вычисление координат узловой точки 17

В табл. 32 — 34 приведен пример уравнивания системы теодолитных ходов с одной узловой точкой.

Таблица 33

Вычисления окончательного значения дирекционного угла узловой линии 011

		Число	Вес, / Л= —
№ хода	Дирекцион. углы, й?	углов в ходе,		е.	Р1С,		Вычисления
1 2	100°32,4' 33,5'	3 5	0,33 0,20	0,0' М'	0,00' 0,22'	+0,8' -0,3'	ади=а0+^ = 100*32,4' +
3	33,8'	3	0,33	1,4'	0,46'	-0,6'
ао =	= 100°32,4'		0,86		= 0,68		+0,8'= 100° 33,2'

\о,33-0,8² +0,20-0,3² +0,33-0,б²

Таблица 34

№ хода	Длина хода	Вес,	х', м	е м	рех, м	У', м	Ву, м	рсу, м
1	0,61	1,64	5952,30	0,71	1,16	2837,11	0,00	0,00
2	1,27	0,79	5951,68	0,09	0,07	2837,51	0,40	0,32
3	0,74	1,35	5951,59	0,00	0,00	2837,92	0,81	1,09
	М = 3,78		= 5951,59	\рех\= 1,23 Уо"		= 2837,11	[ре,]- 1,41

ГШ Н. ШЦЕШЕ тппж ШШ СЕТЕ1

[Р'х]

Ы

^хи ~~ ^хо +

= 5951,59 + 0,33 = 5951,92 м, у_и = 2837,11 + 0,37 = 2837,48м.