Раздел II. Геодезические работы ва еряыш территории

• осевой меридиан зоны и экватор изображаются на плоскости взаим­но перпендикулярными линиями;

• масштаб изображения вдоль осевого меридиана равен единице; с удалением от осевого меридиана он увеличивается, но в каждой точке остается постоянным во всех направлениях.

Выполнение первого условия вызывает искажение (увеличение)

длин линий на плоскости проекции, поэтому вся зона на поверхности эллипсоида отображается на плоскости в несколько расширенном виде (см. рис. 12).

Рис. 12. К понятию равноугольной поперечно-цилиндрической проекции Гаусса — Крюгера

Н,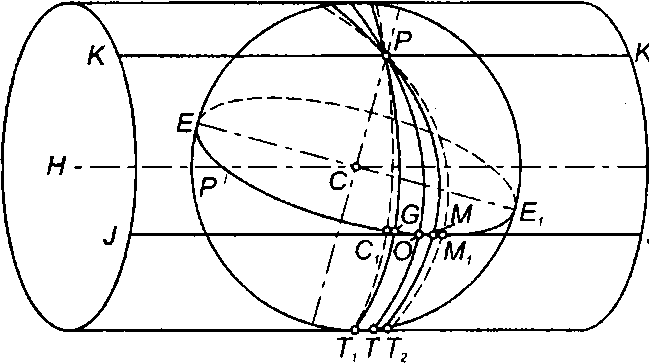

В результате такого проектирования получают изображение поверх­ности земного шара (эллипсоида) в виде 60 зон, примыкающих друг к другу на экваторе (рис. 13). Каждая из этих зон представляет собой прямоугольную систему координат со своим началом координат —

точкой пересечения экватора с осевым меридианом зоны. Такая система получила название зо­нальной системы плоских прямо­угольных координат Гаусса — Крюгера.

Рис. 13. Зональная система плоских прямоугольных координат: изображение координатных зон на плоскости проекции

Масштаб изображения в проек­ции Гаусса - Крюгера. Как отме­чено выше, данная проекция явля­ется равноугольной, т. е. в ней не искажаются углы геометрических фигур. В то же время длины линий (кроме дуг осевых меридианов) и площади контуров проектируют­ся с поверхности эллипсоида на плоскость проекции с искаже­ниями. О величине искажения длин линий судят по величине масштаба изображения в плоско­сти проекции.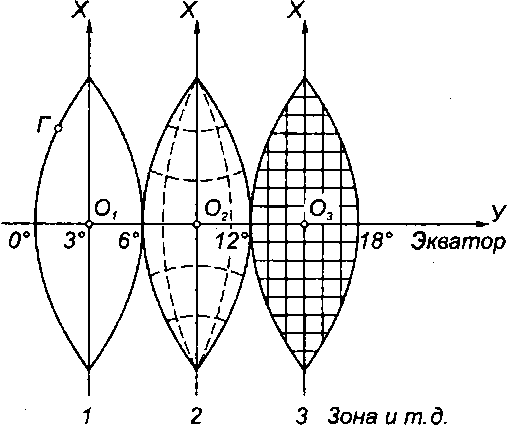

тп 5. ИСТШИ111ЦЩТ

Масштаб изображения в данной точке — это предел отношения бесконечно малого линейного элемента з_г проекции к соответствующе­му элементу з поверхности эллипсоида (шара), т. е.

(102)

Масштаб изображения не является постоянной величиной. Он ра­вен единице на осевом меридиане и увеличивается по мере удаления от него. Закономерность изменения масштаба изображения в пределах зоны можно установить из следующих соображений.

Представим Землю в виде шара, помещенного в цилиндр и касающе­гося его поверхности по осевому меридиану РОР₁ (см. рис. 14, а). Ось цилиндра НН₁ совпадает с диаметром экватора ЕЕ_Г Возьмем на шаре дугу малого круга АВ, расположенную вблизи осевого меридиана и па­раллельную ему. Через точку А проведем дугу большого круга АЕ_Г ко­торая пересечет осевой меридиан в точке А₀. Через точки А₀иО прове­дем образующие цилиндра КЬ и СЫ и примем их за изображения дуг больших кругов А₀Е₁ и ОЕ₁ на цилиндре.

а

б

Рис. 14. Переход от сферических прямоугольных координат к плоским прямоугольным координатам в проекции Гаусса—Крюгера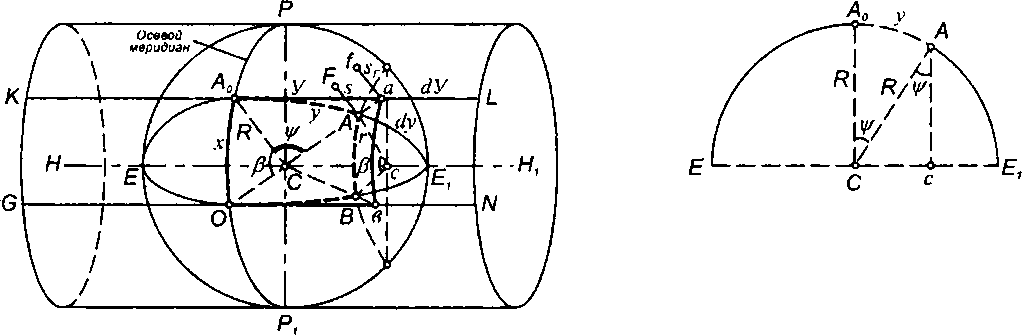

Приняв линии осевого меридиана и экватора за оси координат, положение точки А на шаре можно определить длинами дуг больших

кругов АВо и А₀А = у , которые представляют собой сферические пря­моугольные координаты точки А (см. § 18). Точкам А и В на шаре будут

соответствовать точки а и Ь на плоскости цилиндра.

В равноугольной проекции изображение бесконечно малой фигуры вокруг любой точки на цилиндре должно быть подобным соответствую­щей фигуре на шаре. Это возможно, если отношение длин бесконечно малых отрезков на проекции, выходящих из какой-либо точки, к длинам соответствующих отрезков на шаре будет постоянным, т. е. масштаб изображения в окрестности точки одинаков во всех направлениях.

Согласно рис. 14, а дута на шаре, заключенная между дугами А₀Е_Х

и ОЕ_х , уменьшается по мере удаления точки А от осевого меридиана,

тт ii. геодезические ийты 1д шми шш

тогда как расстояние между образующими на цилиндре остается по­стоянным. Отсюда следует, что для сохранения подобия отрезок А₀а должен быть больше дуги А₀А шара, причем относительное увеличение

тем больше, чем дальше точка А отстоит от осевого меридиана.

Возьмем два соответствующих малых отрезка: АР = з на шаре и а/ = 8_Г на цилиндре. В конформной проекции для любого направления из точки А должно выполняться условие

/и = -7 = соти (103)

и

Приняв, что дуга АВ достаточно мала, в соответствии с выражением (103) можно записать

а/ _ аЪ

Г.Г. Доклад С.П. Гриднев 1

ГЕОДЕЗИЯ 1

ГЕОДЕЗИЯ 6

Глава 8 70

ГЕОДЕЗИЧЕСКИЕ ИЗМЕРЕНИЯ И ИХ ТОЧНОСТЬ 70

§ 28. Процессы производства геодезических работ 70

§ 29. Единицы измерений, применяемые в геодезии 71

§ 30. Понятие о погрешностях измеренных величин и характеристиках точности измерений 72

§ 31. Требования к оформлению результатов полевых измерений и их обработке 75

Глава 9 81

УГЛОВЫЕ ИЗМЕРЕНИЯ 81

§ 32. Принцип измерения горизонтальных и вертикальных углов 81

§ 33. Классификация теодолитов 82

§ 34. Принципиальная схема устройства теодолита 84

§ 35. Горизонтальный круг. Отсчетные устройства 85

§ 36. Зрительные трубы 90

§ 37. Уровни 95

§ 38. Вертикальный круг теодолита 101

§ 39. Устройство технических теодолитов 109

§ 40. Поверки и юстировки теодолита 112

§ 41. Установка теодолита в рабочее положение 126

§ 42. Измерение горизонтальных углов 126

§ 43. Погрешности измерения горизонтальных углов 129

§ 44. Измерение вертикальных углов 106

§ 45. Измерение теодолитом магнитного и истинного азимутов направлений 108

§ 46. Понятие об электронных и лазерных теодолитах 113

Глава 10 10

ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ 10

§ 47. Способы измерения длин линий 10

§ 48. Механические приборы для непосредственного измерения длин линий 10

§ 49. Компарирование мерных приборов 120

§ 50. Понятие о свето- и радиодальномерах 122

§ 51. Оптические дальномеры. Нитяной дальномер 124

Глава 11 12

ОБЩИЕ СВЕДЕНИЯ О ГЕОДЕЗИЧЕСКИХ СЪЕМКАХ 12

Глава 12 10

ТЕОДОЛИТНАЯ СЪЕМКА. ПОЛЕВЫЕ РАБОТЫ 10

Глава 13 178

КАМЕРАЛЬНЫЕ РАБОТЫ ПРИ ТЕОДОЛИТНОЙ СЪЕМКЕ 178

, -Лбе_ Ул²+л² 3

ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ ЗЕМЕЛЬНЫХ УГОДИЙ 189

§ 71. Аналитический способ определения площадей 189

§ 72. Графический способ определения площадей 190

§ 73. Механический способ определения площадей 194

§ 74. Измерение площади планиметром 199

§ 75. Порядок определения площадей земельных угодий, их увязка и составление экспликации 204

Глава 15 206

ГЕОМЕТРИЧЕСКОЕ НИВЕЛИРОВАНИЕ 206

§ 76. Сущность и способы геометрического нивелирования 206

§ 77. Влияние кривизны Земли и рефракции на результаты геометрического нивелирования 210

§ 78. Нивелиры и их классификация 213

§ 79. Нивелирные рейки. Установка реек в отвесное положение 214

§ 80. Устройство нивелиров 217

§ 81. Поверки и юстировки нивелиров 221

§ 82. Основные источники погрешностей геометрического нивелирования 224

§ 83. Нивелирование III и IV классов 227

§ 84. Техническое нивелирование 230

§ 85. Продольное инженерно-техническое нивелирование 231

§ 86. Обработка журналов нивелирования 250

§ 87. Составление профиля трассы 232

§ 88. Нивелирование поверхности 236

§ 89. Понятие о лазерных и цифровых нивелирах 245

МЕНЗУЛЬНАЯ СЪЕМКА 240

§ 90. Сущность мензульной съемки 240

Глава 16 240

§ 91. Приборы, применяемые при мензульной съемке 243

§ 92. Поверки мензулы и кипрегеля 246

§ 93. Установка мензулы в рабочее положение 249

§ 94. Подготовительные работы при мензульной съемке 250

§ 95. Создание сети съемочного обоснования 251

§ 96. Съемка ситуации и рельефа 267

Глава 17 271

ТАХЕОМЕТРИЧЕСКАЯ СЪЕМКА 271

§ 97. Сущность тахеометрической съемки 271

§ 98. Приборы, применяемые при тахеометрической съемке 272

§ 99. Создание сети съемочного обоснования 280

§ 100. Съемка ситуации и рельефа 281

§ 101. Камеральные работы при тахеометрической съемке 287

Глава 18 290

АВТОМАТИЗИРОВАННЫЕ МЕТОДЫ СЪЕМОК 290

§ 102. Понятие об автоматизированных методах топографических съемок 290

§ 103. Электронная тахеометрическая съемка 295

§ 104. Определение положения точек земной поверхности с помощью геодезических спутниковых систем 300

§ 105. Понятие об автоматизированных способах построения плана по цифровой модели местности 307

Глава 19 12

ГЕОДЕЗИЧЕСКИЕ РАБОТЫ НА СТРОИТЕЛЬНОЙ ПЛОЩАДКЕ ПРЕДПРИЯТИЙ 12

§ 106. Этапы геодезических работ при строительстве сооружений 12

§ 107. Составление проекта вертикальной планировки строительной площадки 14

§ 108. Геодезическая подготовка данных для перенесения проекта в натуру 23

§ 109. Строительная координатная сетка 308

§ 110. Элементы геодезических разбивочных работ 311

ГЕОДЕЗИЧЕСКИЕ РАЗБИВОЧНЫЕ РАБОТЫ 311

§111. Перенесение проектных отметок на рабочие горизонты 317

§ 112. Способы перенесения в натуру точек и осей сооружений 320

т_й = ту]2, 52

2 = р% 1П0, 143

§ 20. Системы координат Государственного земельного кадастра 40

§ 21. Преобразование координатных систем 41

Глава 6 53

ОПОРНЫЕ ГЕОДЕЗИЧЕСКИЕ СЕТИ 53

§ 22. Классификация геодезических опорных сетей 53

§ 23. Традиционные методы построения государственных геодезических сетей 54

§ 24. Геодезические сети сгущения и съемочные сети 62

§ 25. Совершенствование системы геодезического обеспечения в условиях перехода на спутниковые методы координатных определений 63

§ 26. Геодезическая основа межевания земель 64

§ 27. Закрепление и обозначение на местности пунктов геодезических сетей 65

Глава 7 26

СОЗДАНИЕ И РЕКОНСТРУКЦИЯ СПУТНИКОВЫХ ГОРОДСКИХ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ 26

§ 28. Городские сети и их классификация 26

§ 29. Требования к закреплению пунктов спутниковых городских геодезических сетей 29

§ 30. Основные принципы построения спутниковых городских геодезических сетей 30

§ 31. Наблюдения на пунктах спутниковой сети 33

§ 32. Предварительная обработка спутниковых наблюдений 36

§ 33. Городская полигонометрия 37

§ 34. Обработка и уравнивание городских геодезических сетей. Составление каталогов координат 38

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ДОПОЛНИТЕЛЬНЫХ ОПОРНЫХ ПУНКТОО 43

§ 35. Прямые геодезические угловые засечки 43

§ 36. Обратная геодезическая засечка (задача Потенота) 436

§ 37. Комбинированная геодезическая засечка 453

Глава 9 29

УГЛОВЫЕ ИЗМЕРЕНИЯ В ГЕОДЕЗИЧЕСКИХ СЕТЯХ СГУЩЕНИЯ 29

г = +0,3' 190

Глава 10 219

ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ В СЕТЯХ СГУЩЕНИЯ 219

ПРЕДВАРИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ В СЕТЯХ СГУЩЕНИЯ 509

ОБЩИЕ СВЕДЕНИЯ ОБ УРАВНИВАНИИ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ 34

УПРОЩЕННОЕ УРАВНИВАНИЕ ТИПОВЫХ ФИГУР ТРИАНГУЛЯЦИИ 536

УПРОЩЕННОЕ УРАВНИВАНИЕ СЪЕМОЧНЫХ СЕТЕЙ 561

1>₃=Н_Г-~Н₃, »₄=Н₄-Н_Г 597

СПИСОК ЛИТЕРАТУРЫ 581

предметны! указатель 583

Подставив в выражение (122) формулы (123) и (124), имеем

'=77<¹²⁵>

Поскольку I представляет собой разность долгот меридиана точки С и осевого меридиана зоны, т. е. / = (Ь — 1₀), то выражение (125) можно записать как

/ = (2,-^)81115. (126)

Как следует из выражения (126), сближение меридианов в восточ­ной части зоны будет положительным, а в западной — отрицательным. При этом абсолютная величина у возрастает по мере удаления точки от осевого меридиана.

Погрешность определения величины уио формуле (126) не превыша­ет 4" для 6-градусной зоны и 0,5" — для 3-градусной зоны.

При переходе от азимута к дирекционному углу направления по полной формуле (121) величина поправки в направление д_г за кривизну изображения линии в проекции (см. рис. 16) определится по формуле

<*г=Г-{хи-Хн)у^ (127)

где Г = ^ = 0,00254;_Лр = >^±>^,

Максимальная погрешность вычисления З_г по формуле (127) при длине стороны до 10 км не превышает 0,03"; при этом значение коор­динат можно брать с точностью до 0,1 км. При геодезических работах по развитию сетей сгущения и созданию съемочного обоснования поправкой 8_Г обычно пренебрегают ввиду ее малости.

Перевычисление координат Гаусса-Крюгера из одной зоны в дру­гую. Перекрытие зон. Каждая зона представляет собой самостоятель­ную систему координат. При уравнивании обширных геодезических сетей часть исходных пунктов может располагаться в одной зоне, а другая — в смежной с ней зоне. В этом случае возникает необходи-

тт II. ГЕОДЕЗИЧЕСКИЕ РАБОТЫ ИД ИЛЬИН ТЕРШИМИ

мость перевычисления (преобразования) координат пунктов из одной зоны в другую, чтобы получить координаты всех пунктов в системе координат одной зоны. Обычно перевычисление выполняют в ту зону, в которой число пунктов сети больше.

Аналогичная задача возникает также при переходе из 6-градусной зоны в 3-градусную зону, осевым меридианом которой служит гранич­ный меридиан двух смежных 6-градусных зон.

Чтобы уменьшить необходимость перевычисления координат из зоны в зону, на границах координатных зон установлена полоса перекрытия (рис. 18). Для этой полосы координаты пунктов, располо­женных в пределах ±30* от граничного меридиана, вычисляют одновре­менно в двух смежных зонах; на топографических картах, распо­ложенных в полосе перекрытия, кроме основной сетки показывают выходы координатных сеток смежных зон.

Существует несколько спо­собов преобразования коорди­нат из одной зоны в другую.

1. Перевычисление коорди­нат с предварительным пере­ход ом к геодезическим коорди­натам. Идея способа состоит в том, что от плоских прямоуголь­ных координат пункта одной зоны переходят к его геодези­ческим координатам (в, I), а от них — к плоским координатам смежной зоны.

для

Пусть пунктА (см. рис. 18) с координатами х₁, у₁ расположен в 1-й зоне; требуется вычислить координаты х₂, у₂ этого пункта во 2-й зоне. Сначала по извест­ным координатам х_]г у₁ пункта в 1-й зоне с осевым меридианом Ь_о1 вы­числяют его геодезические координаты В и Ь-Ь_0х +/_г Затем относитель-

но осевого меридиана 2-й зоны 1^=1^+6° (либо Ь =Ь +3°

3-градусной зоны) находят разность долгот /₂ =1-Ь_0г. Далее от геодези­ческих координат переходят к прямоугольным коордцнатам х₂, у₂ пунк­та во 2-й зоне.

Данный способ является наиболее строгим и универсальным. Учи­тывая большой объем вычислений, его использование целесообразно при решении задач преобразования прямоугольных координат в геоде­зические и обратно на ЭВМ по специальным программам.

2. Перевычисление координат путем редуцирования горизонтальных направлений. Этот способ применяют в случаях, когда необходимо пре­образовать координаты большого числа пунктов из одной зоны в другую.

Рис. 18. Перекрытие зон в проекции Гаусса — Крюгера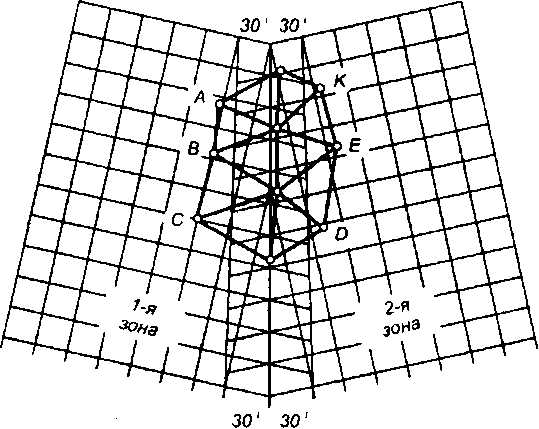

Не менее чем для двух исходных пунктов по первому способу пере­вычисляют координаты из 1-й зоны во 2-ю. Используя полученные

пш 5. систему иццимт

координаты, находят приближенные координаты других пунктов и по ним вычисляют поправки в измеренные направления за кривизну изоб­ражения линий 8" во 2-й зоне. Исправив измеренные направления по­правками 8"— 8} (здесь 8'_{ — поправки за кривизну изображения линий в 1-й зоне), получают направления, отнесенные ко 2-й зоне. Выполнив уравнивание сети по исправленным направлениям, вычисляют коорди­наты всех пунктов в системе координат 2-й зоны.

3. Перевычисление координат пунктов с помощью специальных таблиц. Ранее этот способ широко применялся при ручном перевычис­лении координат пунктов. Наибольшее распространение получили таб­лицы А.М. Вировца и Б.Н. Рабиновича, С.П. Герасименко и А.В. Буш- кевича и др., позволяющие перевычислять координаты из одной зоны в другую с точностью до 2 — 3 см.