Типы входных потоков

Наиболее распространенным являются простейшие (пуассоновские) потоки. Поток однородных событий называется простейшим, если он обладает тремя свойствами: стационарностью, ординарностью и отсутствием последействия. Простейший поток описывается пуассоновским законом распределения вероятностей наступления и событий на интервале времени t

,

где P(k, t)— вероятность того, что за время t в систему поступит ровно k заявок.

Модель обслуживания, рассматриваемая в работе

Входной поток ТК образуется заявками на ремонт и наладку от четырех компонентов комплекса: станков с программным управлением, промышленных роботов, программных транспортных устройств и управляющих ЭВМ (число входных потоков однородных событий равно четырем.)

Функционирование системы связано как с плановыми ремонтами, так и ремонтами при внезапных отказа технических средств, и, в общем случае, входные потоки следует рассматривать как потоки Эрланга с параметрами . В случае упрощенных расчетов можно исследовать предельный случай и рассмотреть входные потоки как потоки Пуассона с параметрами = 1,

Длительность выполнения заявки для каждого компонента определяется величиной 1/ , возникающие при обслуживании стоимостные потери связаны со штрафами за единицу времени простоя заявки каждого потока в очереди. Обозначим их - .

Характеристики бесприоритетных дисциплин обслуживания.

При бесприоритетной дисциплине обслуживания заявки разных типов не имеют заранее определенных привилегий на обслуживание. Это правило выполняется, если

1) заявки на обслуживание выбираются в порядке поступления (первой обслуживается заявка, поступившая раньше других — дисциплина FIFO)

2) в порядке, обратному порядку поступления (первой обслуживается заявка, поступившая раньше других — дисциплина LIFO).

3) наугад, т.е. путем случайного выбора из очереди.

Эти три бесприоритетных дисциплины характеризуются одинаковым средним временем ожидания заявок, но дисциплина FIFO минимизирует дисперсию времени ожидания, поэтому используется при расчетах наиболее часто.

Пусть в систему поступают заявки М типов с интенсивностями . Предположим, что каждый входящий поток— пуассоновский. В таком случае суммарный поток заявок также пуассоновский и его интенсивность

Пусть также известны математические ожидания и вторые начальные моменты времени обслуживания заявок типа 1,..М соответственно. Эти значения характеризуют распределение времени выполнения соответствующих программ. Тогда при использовании бесприоритетной дисциплины обслуживания среднее время ожидания заявок всех типов одинаково и равно

,

R = ( ) < 1—суммарная загрузка системы и .

Характеристики дисциплин обслуживания с относительными приоритетами

Если требуется, чтобы заявки некоторого типа имели меньшее время ожидания (время обслуживания), чем заявки других типов, то необходимо первым представить преимущественное право на обслуживание, называемое приоритетом. Приоритеты заявок характеризуются целыми положительными числами, причем высокому приоритету соответствует меньшее число.

Если приоритеты учитываются только в момент выбора заявки на обслуживание, то их называют относительными. Если в систему поступает М простейших потоков с интенсивностями и длительности обслуживания заявок каждого потока имеют математические ожидания и вторые начальные моменты , соответственно, то среднее время ожидания заявок, имеющих приоритеты k=l, .. .М, определяется по следующей формуле

,

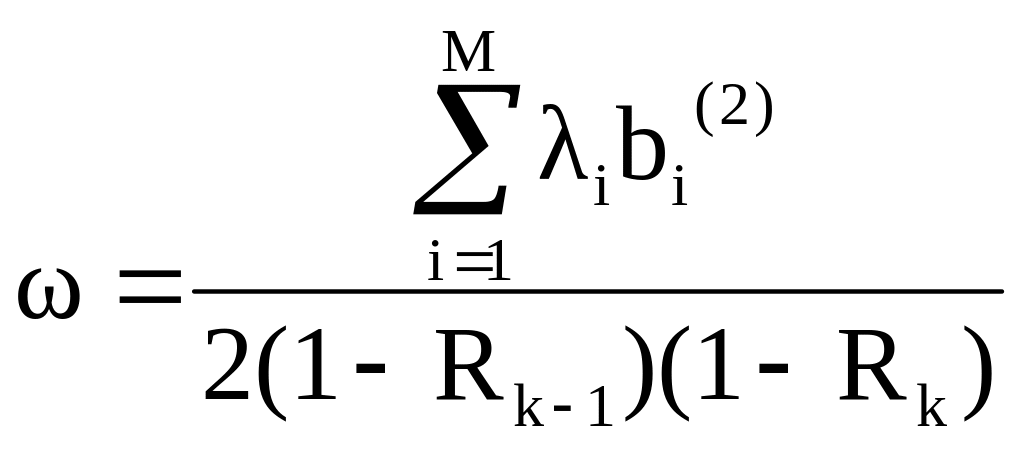где b, R — загрузки, создаваемые потоками заявок.

Характеристики дисциплин обслуживания с абсолютными приоритетами.

В ряде случаев время ожидания заявок некоторых типов нужно уменьшить в такой степени, которая недостижима при использовании относительных приоритетов. Время ожидания можно сильно уменьшить, если при поступлении высокоприоритетной заявки обслуживание ранее поступившей заявки с низким приоритетом прерывается, и процессор тут же предоставляется для обслуживания высокоприоритетной заявки. Такая дисциплина обслуживания называется обслуживание с абсолютными приоритетами. Обслуживание прерванных заявок может проводиться от начала или от момента прерывания (дообслуживание). Если потоки заявок - простейшие с интенсивностями , а математические ожидания времен обслуживания равны , вторые начальные моменты - , соответственно, и прерванные заявки дообслуживаются от точки прерывания, то среднее время ожидания заявки с абсолютным приоритетом k=l, .. .М

,

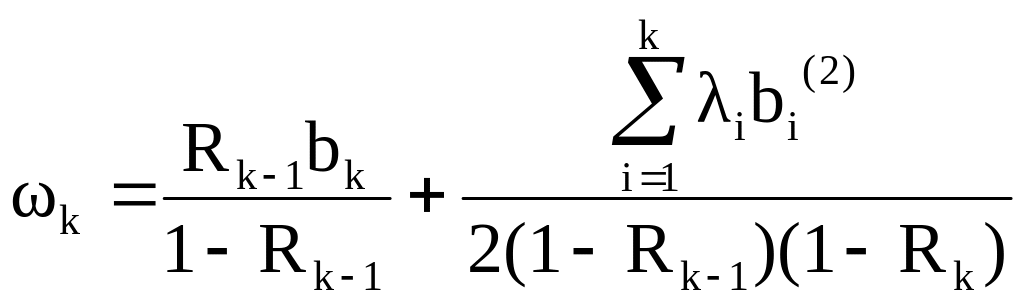где b R — загрузки, создаваемые потоками заявок.

Характеристики дисциплин обслуживания со смешанными приоритетами.

В некоторых системах необходимо выполнить жесткие ограничения на время ожидания отдельных заявок, что требует присваивания абсолютных приоритетов. В результате этого время ожидания низкоприоритетных заявок может оказаться недопустимо большим, хотя отдельные заявки и имеют запас по времени ожидания. Чтобы выполнить ограничения по всем видам заявок, можно наряду с абсолютными приоритетами некоторым заявкам присвоить относительные приоритеты, а остальные заявки обслуживать без приоритетов. Такая дисциплина обслуживания называется смешанная.

Таким образом, рассматривается смешанная дисциплина обслуживания с двумя классами заявок, когда заявкам типа l,...Mi присвоены абсолютные приоритеты, заявкам Mi+l,...M — относительные приоритеты.

Для заявок первого класса, обладающих абсолютными приоритетами по отношению ко всем остальным заявкам, характерна независимость среднего времени ожидания от характеристик заявок с более низкими приоритетами. В этом случае среднее время ожидания заявок первого класса будет таким же, как и при использовании чистой дисциплины обслуживания с абсолютными приоритетами.

Заявки второго класса могут рассматриваться как заявки с относительными приоритетами, время ожидания которых увеличено за счет прерывания заявками первого класса.

Таким образом,

(k=1,2…M₁)

(k= M₁…M)

3 Порядок выполнения работы

3.1. Провести расчет исследуемой системы с использованием аналитического подхода, как одноканальной СМО с ожиданием и без приоритетов. Интенсивность входного потока в этом случае равна

Средневзвешенная длительность обслуживания -

Среднее время ожидания

Суммарные потери - L =

3.2. Определить оптимальные относительные и абсолютные относительные приоритеты

3.3. Рассчитать параметры системы для смешанных приоритетов

3.4. Вычислить среднее время ожидания для каждого потока, суммарные потери для различных видов приоритетов. Результаты свести в таблицу. Провести анализ эффективности приоритетных СМО и выбрать наилучшую.

Таблица

Тип приоритета	1	2	3	4	L
Обслуживание без приоритетов
Относительные приоритеты
Абсолютные приоритеты
Смешанные приоритеты

4 Практическая часть

ЗАДАНИЕ

4.1 Ознакомьтесь с материалами, приведенными в теоретической части работы.

4.2 Выберите вариант задания из нижеприведенной таблицы. Номер варианта должен соответствовать номеру студента в списке группы.

4.3 Произведите все необходимые расчеты по определению времен ожидания для заявок с различными приоритетами, занести результаты расчетов в таблицу 1 и выбрать наилучшую дисциплину обслуживания по критерию минимума стоимостных потерь от ожидания заявок в очереди.

4.4 Оформите отчет и защитите работу.

5 Содержание отчета

Отчет должен содержать:

5.1 Постановку задачи исследования.

5.2 Расчетные программы определения временных характеристик системы с различными вариантами приоритетов и стоимостей потерь для каждого варианта

5.3 Выводы по работе.

5. Контрольные вопросы

1. Что такое неоднородный поток? Приведите пример неоднородного потока.

2. Какие приоритеты называются относительными, что дает введение таких приоритетов?

3. Какие приоритеты называются абсолютными, что дает их использование?

4. Нарисуйте примерный график зависимостей времени ожидания от загрузки для ИС с тремя потоками заявок и относительными приоритетами между ними. После этого поменяйте приоритеты на абсолютные. Как изменятся нарисованные Вами графики?

2.5 Лабораторная работа № 5 Определение оптимальной дисциплины обслуживания для информационных систем с ограничениями на время ожидания.

Находится в разработке

2.6 Лабораторная работа № 6 Сетевые модели массового обслуживания

1 Цель работы

Данная работа является ознакомительной и имеет целью первоначальное знакомство студентов с аппаратом сетей массового обслуживания, его использованием для описания информационных систем, а также с инструментальными средствами, применяемыми для автоматизации расчетов и анализа подобных систем.

2 Основные теоретические положения

Исследуемую систему обработки спутниковой информации можно рассматривать как совокупность устройств, процессы функционирования которых описываются с помощью методов и моделей теории массового обслуживания. При этом каждое устройство представляется в виде системы массового обслуживания (СМО), что требует задания ряда характеристик СМО. В их число входят законы распределения параметров поступления и обработки заявок, количество каналов обработки, число мест ожидания в буферном накопителе, число типов заявок, поступающих в систему, дисциплина обслуживания заявок и др.

Значительное количество характеристик, необходимых для описания СМО, предопределяет большое число классов систем, сложность аналитического моделирования которых является весьма различной.

Наиболее просто исследовать системы массового обслуживания, относящиеся к классу марковских одно и многоканальных систем с заявками одного типа, бесконечным количеством мест ожидания в очереди и обслуживанием в порядке поступления. Функции распределения параметров поступления и обработки заявок в таких СМО являются экспоненциальными и имеют следующий вид:

(1)

(2)

где l и m называются, соответственно, интенсивностью поступления и обработки заявок и показывают средне количество заявок, поступивших и обработанных в СМО в единицу времени.

СМО этого типа имеют стандартное обозначение М/M/1 или M/M/K, где К - число каналов обработки в СМО. Если в качестве СМО представить каждое устройство системы обработки спутниковой информации и связать их в единую сеть в соответствие с характером информационной обработки в условиях неопределенности прохождения задачи по сети, то получим совокупность взаимосвязанных СМО, которую называют стохастической сетью.

Математический аппарат теории экспоненциальных стохастических сетей развит к настоящему времени достаточно хорошо, что позволяет использовать его на практике при исследовании различных информационных систем (ИС).

В зависимости от характера и принципа организации ИС, а также способов обработки информации могут использоваться стохастические сети двух типов: разомкнутые и замкнутые.

Под разомкнутой стохастической сетью (РСС) понимается сеть, в которой интенсивность внешнего источника заявок не зависит от того, сколько заявок уже находится в сети.

Модели замкнутых стохастических сетей характеризуются зависимости интенсивности источника заявок от количества заявок, находящихся в сети, причем количество заявок в сети остается постоянным.

В настоящей работе мы рассмотрим только разомкнутые сети.

Стохастические сети описываются совокупностью параметров, в состав которых входят: число n систем массового обслуживания , образующих сеть; число каналов (обслуживающих приборов) в системах ; матрица вероятностей передач ; интенсивность обслуживания (i=1..n) заявок в узлах сети или средняя длительность обработки , где ; интенсивность источника заявок в РСС.

Рассмотрим под­робнее способы определения и физический смысл перечисленных параметров, используемых при построении стохастической сетевой модели информационной системы.

1. Количество узлов в сети (n) выбирается равным числу устройств обработки, входящих в рассматриваемую систему.

2. Количество каналов обработки системах (i=1..n) сети определяются по числу однотипных устройств системы, выполняющих идентичные функции при обработке потока заявок;

3. Стохастической матрицей передач устанавливаются связи между СМО сети на основе анализа порядка следования этапов обработки в ходе выполнения вычислительного процесса.

Для учета неопределенности маршрута передачи заявки из общего потока дугам направленного графа передачи заявок (вершинам графа соответствуют СМО сети, а дугам - связи между ними) ставится в соответствие вероятности перехода , которые образуют матрицу переходов P (n+1)x(n+1). Каждый элемент матрицы Р показывает вероятность того, что заявка, закончив обработку в системе , поступит в систему . Если в системе такой переход обязателен, то =1, если он недоступен, то =0.

Поскольку потери заявок в сети отсутствуют, то должно выполняться условие для всех i=0..n.

4. Интенсивность обслуживания (i=1..n) показывает среднюю скорость обработки заявок в каждом канале системы ( величина обратная среднему времени обслуживания заявки ; ). Величина в СМО определяется средними трудоемкостями (i=1..n) решения задачи системой и быстродействием (i=1..n) устройств, входящих в систему и вычисляется по формуле .

Перечисленные характеристики исчерпывают всю необходимую информацию, которая требуется для аналитического моделирования.

Аналитические методы исследования экспоненциальных стохастических сетей основываются на двух фундаментальных теоремах. Первая из них, известная как теорема Бирке, говорит о том, что исходящий поток стационарной СМО типа M/M/K с пуассоновским входным потоком с интенсивностью l и экспоненциальным распределением времени обслуживания с параметром m в каждом из K каналов обработки является пуассоновским потоком с тем же параметром l.

Вторая теорема, названная именем Дж. Джексона, используя результаты П.Берке, доказывает, что в стохастической сети с известными вероятностями перехода , каждый узел, которой представляет собой СМО типа M/M/K, можно рассматривать независимо от другого. Т.е. удалось показать, что , где - вероятность одновременного пребывания в i-ой СМО заявок (i=1..n), а - вероятность пребывания в i-м узле сети заявок.

Рассмотренные теоремы заметно облегчают исследование сетевых моделей как совокупности СМО, поскольку позволяют исследовать сеть без учета влияния отдельных систем друг на друга.

Для определения характеристик СМО в сети, а также характеристик самой сети необходимо найти интенсивности входных потоков заявок поступающих в каждый узел. Параметры однозначно определяются значением (интенсивностью источника) и топологией сети (задаваемой матрицей P). В установившемся режиме справедливо равенство (i=0..n), которое в векторной форме имеет вид .

Используя понятие единичной матрицы , где символ Кронекера равен:

æ 0, i¹j

= í

è 1, i=j

получим

. (3)

Откуда система алгебраических уравнений (n+1) порядка относительно в канонической форме имеет вид:

æ (4)

ç

í …………………………..

ç……………………………

è

Зная для РСС значение , можно однозначно определить из этой системы значение (i=1..n).

При определении параметров РСС необходимо, прежде всего, убедится в существовании в сети стационарного режима. Стационарность режима функционирования сети определяется значениями коэффициентов загрузки СМО , образующих настоящую сеть. Значение вычисляется по формуле:

. (5)

Тогда условие существования в сети стационарного режима запишется в следующем виде:

,

где называется коэффициентом передачи.

При определении характеристик разомкнутой экспоненциальной сети используется понятие ее состояния. Под состоянием сети понимается вектор , характеризующий распределение заявок, находящихся в сети, среди систем . Состояние соответствует случаю, когда в системе находится , в системе находится заявок и в системе находится заявок. Заявки в системе обслуживаются приборами этой системы и стоят в очереди на обслуживание.

В стационарном режиме вероятность состояния разомкнутой экспоненциальной сети определяется произведением вероятностей состояний составляющих сеть систем, причем вероятности состояний систем определяются для случая, когда каждая из систем функционирует независимо. Пусть - вероятность того, что в системе находится заявок. Тогда вероятность состояния сети

, где

(6)

где определяет среднее число занятых каналов и вычисляется по формуле:

(7)

(8)

æ при

í (9)

è , при

Окончательно получим

(10)

На основе вероятностей состояний определяются все основные операционные характеристики СМО.

Для СМО M/M/K основные расчетные формулы имеют вид:

- среднее количество заявок, ожидающих обслуживание в системе, т.е. средняя длина очереди в СМО.

(11)

- среднее число заявок, находящихся в системе

(12)

- среднее время ожидания заявки в очереди

(13)

- среднее время пребывания заявки в системе

(14)

Для одноканальных СМО M/M/1 указанные характеристики вычисляются по упрощенным формулам:

(15)

(16)

; (17)

; (18)

. (19)

Определив характеристики отдельных систем можно вычислить характеристики системы в целом.

Тогда

; ;

Изложенный в данном разделе математический аппарат может быть эффективно использован для исследования информационных системы.

3. Порядок выполнения работы

3.1. Изучить теоретическую часть работы.

3.2. Ответить на контрольные вопросы.

3.3. Ознакомиться с принципами работы инструментального средства для анализа РСС – пакетом программ «Сеть».

3.4 Определить характеристики предложенной преподавателем стохастической сети.

3.5 Оформить отчет и сдать работу преподавателю.

4 Практическая часть

Задание

4.1 Ознакомьтесь с материалами, приведенными в теоретической части работы.

4.2 Выберите вариант задания из нижеприведенной таблицы. Номер варианта должен соответствовать номеру студента в списке группы.

4.3 Используя пакет программ «Сеть», произведите все необходимые расчеты по определению среднего времен ответа для заявок без приоритетов, и определите необходимые размеры буферов в каждой СМО сети. Если окажется, что для Ваших исходных данных в сети отсутствует стационарный режим, то измените число каналов обслуживания в тех системах, где загрузка превышает 1 или увеличьте в этих системах интенсивность обслуживания.

4.4 Постройте график изменения времени ответа сети от интенсивности входного потока .

4.5 Оформите отчет и сдайте работу преподавателю.

Таблица 1 –Исходные данные для расчетов

Вариант						Р23	P13	P24	P20	Р12
1	2	4	5	6	7	0,1	-	0,2	0,7	-
2	4	8	9	12	14	-	0,2	0,3	0,7	0,8
3	5	10	12	10	11	0,1	-	0,3	0,6	-
4	6	10	14	15	12	-	0,1	0,1	0,9	0,9
5	3	5	6	7	8	0,2	-	0,4	0,4	-
6	4	6	7	8	9	-	0,3	0,1	0,9	0,7
7	8	17	16	17	15	0,2	-	0,4	0,4	-
8	5	12	10	11	12	-	0,3	0,1	0,9	0,7
9	4	7	8	9	10	0,1	-	0,5	0,4	-
10	10	20	22	22	18	-	0,2	0,1	0,9	0,8
11	6	10	12	12	11	0,1	-	0,5	0,4	-
12	5	10	12	12	10	-	0,1	0,2	0,8	0,9
13	8	16	16	20	20	0,2	-	0,4	0,5	-
14	9	12	20	16	18	-	0,1	0,2	0,8	0,9
15	12	20	15	20	15	0,1	-	0,3	0,6	-
16	13	20	15	20	15	-	0,3	0,4	0,6	0,7
17	6	13	15	12	12	0,1	-	0,3	0,6	-
18	6	13	15	12	12	-	0.1	0,2	0,8	0,9
19	7	13	15	12	12	0,3	-	0,1	0,6	-
20	8	14	15	15	12	-	0,3	0,2	0,8	0,7
21	9	14	15	15	12	0,3	-	0,3	0,4	-
22	10	20	29	20	20	-	0,3	0,2	0,8	0,7
23	11	20	29	20	20	0,1	-	0,4	0,5	-
24	12	20	29	20	20	-	0,1	0,2	0,8	0,9
25	7	14	15	15	12	0,2	-	0,5	0,4	-
26	8	14	18	15	12	-	0,2	0,1	0,9	0,8
27	9	20	29	20	20	0,1	-	0,2	0,7	-
28	4	14	15	15	12	-	0,2	0,1	0,9	0,8
29	8	14	15	15	12	0,2	-	0,4	0,4	-
30	10	12	20	16	18	-	0,1	0,3	0,7	0,9
Вариант						Р23	P13	P24	P20	Р12

Кроме заданных в таблице вероятностей переходов, следует принять, что для всех четных вариантов Р₀₁=Р₄₁=Р₃₁=1, а для нечетных, соответственно, Р₀₁=Р₁₂=Р₃₂=Р₄₁=1.

5 Содержание отчета

Отчет должен содержать:

5.1. Постановку задачи исследования.

5.2 Распечатки проведенных расчетов.

5.3 График зависимости времени ответа от изменения интенсивности входного потока.

5.4. Выводы по работе.

5 Контрольные вопросы

1. По каким признакам классифицируются сети массового обслуживания?

2. Какие реальные системы могут быть промоделированы с использованием замкнутых сетей массового обслуживания?

3. Что такое коэффициент передачи, и какой физический смысл он имеет?

4. В каком диапазоне значений может изменяться коэффициент передачи в разомкнутых сетях с обратными связями?

5. Покажите, как вычисляются интенсивности потоков для разомкнутых сетей.

Литература

1. Основы теории вычислительных сетей. Под ред. С.А. Майорова, М., Высшая школа, 1978 г.

2. Конспект лекций по дисциплине «Проектирование информационных систем»

2.7 Лабораторная работа № 7 Проектирование информационных систем с использованием сетевых моделей массового обслуживания (работа рассчитана на 4-6 часов)

1. Цель работы

1.1 Получение навыков разработки математических моделей сложных информационных систем в условиях неполной информации.

1.2 Практическое использование аппарата стохастических сетей массового обслуживания для анализа и проектирования информационных систем.

2. Основные теоретические положения

Основные теоретические положения теории стохастических систем были изложены в предыдущей работе. Остановимся более подробно на применении моделей стохастических систем массового обслуживания для проектирования информационных систем.

Во-первых, любая сложная информационная система проектируется в условиях неполной информации о параметрах входных потоков, структуре системы и параметрах обслуживающих устройств. Поэтому необходимо уметь, используя математические модели и методы, разумные допущения и предположения, беседы с заказчиком (в данном случае таковым является преподаватель) добывать эту недостающую информации. Во-вторых, всегда необходимо исследовать модель проектируемой системы на устойчивость к возможному увеличению входного информационного потока. Наконец, во многих системах часто целесообразно дать предпочтение в обслуживании одним потокам заявок (назначить приоритеты) за счет других. Все эти и многие другие вопросы разрешимы в рамках аналитического моделирования с использованием стохастического аппарата теории массового обслуживания.

Дадим несколько общих рекомендаций, которые могут оказаться полезными при разработке и исследованиях информационных систем.

Так, например, если в информационной системе, модель которой Вы строите, происходит разветвление информационных потоков, и Вы не имеете информации о переходных вероятностях, то следует принять гипотезу о равновероятном разветвлении потоков.

Другой случай, если при моделировании в какой-либо из систем массового обслуживания загрузка превзошла единицу, то это свидетельствует о том, что данная система не справляется с нагрузкой. Вы как проектировщик должны либо увеличить единичную мощность (производительность) устройства обработки данной СМО, либо взять несколько однотипных устройств. Это позволит решить проблему.

Вообще при проектировании ИС следует стремиться к соблюдению принципа «равнопрочности». Суть его состоит в том, чтобы все системы работали при примерно равной нагрузке. В этом случае ни в одной из них не будет чрезмерного скопления заявок. Оптимальный уровень загрузки отдельных СМО равен примерно 0,6 – 0,65.

3 Порядок выполнения работы

Занятие 1

3.1. Изучить теоретическую часть работы.

3.2. Ответить на контрольные вопросы.

3.3. Получить задание и разработать математическую модель ИС

3.4. Обсудить модель с преподавателем и внести в нее необходимые коррективы.

Занятие 2

3.5. Произвести проектирование ИС с использованием пакета программ «Сеть».

3.6. Проанализировать полученные результаты, построить графики зависимости основных характеристик ИС от интенсивности входного потока.

3.7. В случае необходимости рассмотреть возможность введения приоритетов и произвести повторный расчет характеристик ИС для случая приоритетного обслуживания информационных потоков.

3.8. Оформить отчет и сдать работу преподавателю.

4 Практическая часть

1 Изучить полученный вариант задания и выявить недостающие исходные данные.

2 Получить недостающие исходные данные либо путем расчетов, либо путем работы с Заказчиком системы (преподавателем).

3 Разработать математическую модель в виде стохастической сети массового обслуживания.

4 Использую специализированный пакет программ «Сеть», произвести все необходимые расчеты, заполнить таблицы, построить графики.

5 Сформировать облик проектируемой системы и определить ее характеристики.

6 Сделать выводы по работе, оформить отчет и защитить работу.

5. Содержание отчета

1 Отчет должен содержать описание системы, для которой строится математическая модель

2 Принятые в ходе построения модели допущения и предположения.

3 Математическую модель в виде стохастической сети массового обслуживания.

4 Описание экспериментов, проводимых с построенной моделью и их результаты в виде таблиц, графиков.

5 Результат проектирования системы, т.е. структурная схема спроектированной системы с указанием числа элементов каждого типа и их характеристик. Построенная модель системы должна удовлетворять всем требованиям, предъявляемым в задании.

6. Контрольные вопросы

Литература

1 Основы теории вычислительных сетей. Под ред. С.А. Майорова, М., Высшая школа, 1978 г.

2 Конспект лекций по дисциплине «Проектирование информационных систем».

2.8 Лабораторная работа № 9 «Методология функционального моделирования IDEF0»

1 Цель работы

Целью данной лабораторной работы является формирование у студентов представлений о сущности функционального подхода к моделированию на примере задачи анализа бизнес-процессов в заданной предметной области, ознакомление с международными и отечественными стандартами и рекомендациями в данной области («FIPS 183. Integration Definition for Function Modeling (IDEF0)» и рекомендаций по стандартизации Госстандарта России «Р 50.1.028-2001. Методология функционального моделирования ).

В результате выполнения работы студенты должны подтвердить знание следующих элементов методологии IDEF0:

• синтаксис графического языка;

• семантика языка;

• правила построения графических диаграмм модели.

2 Основные теоретические положения

2.1 Описание предметной области на естественном языке

Описание предметной области на естественном языке должно представлять собой связный текст и может включать в себя таблицы и рисунки. В описание должны быть включены все бизнес-процессы, которые предполагается подвергнуть функциональному анализу. В описании важно раскрыть характеристики этих процессов: определения основных участников, последовательности реализующих процедур, организационные и случайные факторы, влияющие на их протекание и т.д.

Описание на естественном языке служит основой для процесса формализации предметной области, реализуемого в ходе построения IDEF0-модели. Модель не может содержать каких-либо аспектов предметной области, не зафиксированных в данном описании.

Раздел описания не может быть озаглавлен как «Описание предметной области». Заголовок должен отражать контент описания. Примеры правильных заголовков: «Описание процессов учёта товаров на складе компании «Норникель»», «Описание порядка начисления зарплаты в МАИ», «Описание процесса испытания сложных технических объектов на испытательной станции»

2.2 Модель IDEF0

Данный раздел должен содержать основные компоненты модели IDEF0, построенные в ходе функционального анализа предметной области: цели и границы моделирования, определения точки зрения разработчика и целевой аудитории, глоссарий предметной области и набор графических диаграмм.

Каждый компонент должен быть оформлен в виде отдельного подраздела отчёта. В зависимости от сложности предметной области и целей проводимого анализа, отчёт может не содержать определений точки зрения разработчика и целевой аудитории или может быть дополнен подразделами с текстовым комментариями к диаграммам.

Цель создания модели

Формулировка цели выражает причину создания модели, то есть содержит перечень вопросов, на которые должна отвечать модель, что в значительной мере определяет её структуру.