Финальные вероятности
Если существует предел
,
то существует и финальная вероятность.
Доказана следующая ТЕОРЕМА о
существовании финальной вероятности.
Если число возможных состояний, в которых может находиться система n, конечно и из каждого состояния за конечное число шагов можно перейти в любое другое, то финальные вероятности существуют.
Финальная вероятность это среднее, относительное время пребывания системы в данном состоянии.
3. Порядок выполнения работы
1. Изучить теоретическую часть работы
2. Составить уравнения Колмогорова для заданного преподавателем варианта задания.
3. С помощью пакета MathCad провести необходимые расчеты и построить графики.
4. Проанализировать полученные графики и сделать выводы по работе
5. Оформить отчет и сдать зачет по работе.
4. Практическая часть
ЗАДАНИЕ
Для графа, заданного преподавателем, составьте систему дифференциальных уравнений Колмогорова.
Решите эту систему для нулевых начальных условий.
Постройте графики зависимостей вероятностей состояний от времени, укажите на нем момент времени, начиная с которого можно считать, система перешла в установившийся режим.
Укажите приблизительно, как связана длительность переходного процесса и параметры потоков, переводящих систему из состояния в состояние.
Оформите отчет и сдайте зачет преподавателю.
Содержание отчета
В отчете приводятся:
5.1 Цель выполнения работы
5.2 Заданный граф состояний и соответствующая ему система дифференциальных уравнений Колмогорова.
5.3. Программа решения системы дифференциальных уравнений и график зависимостей вероятностей состояний от времени.
5.4. Выводы по работе.
Контрольные вопросы
6.1 Что мы получим, решив систему дифференциальных уравнений Колмогорова для вероятностей состояний?
6.2 При каких условиях существуют финальные вероятности?
6.3 В каком случае дифференциальные уравнения Колмогорова преобразуются в систему алгебраических уравнений? Объясните физический смысл этого превращения.
6.4 Каков физический смысл (что показывает) финальная вероятность?
6.5 Какие параметры системы влияют на длительность переходного процесса?
Литература
Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и ее инженерные приложения. – М.: Наука, 1991.
Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания. – 2-е изд., перераб. и доп. - М.: Наука: Гл.ред. физ.-мат. лит., 1987. – 336 с.
Клейнрок Л. Теория массового обслуживания. /Пер. с англ. И.И. Грушко; ред. В.И. Нейман. – М.: Машиностроение, 1979. – 432 с., ил.
Фомин Г.Ф. Системы и модели массового обслуживания в коммерческой деятельности: Учеб. пособие. – М.: Финансы и статистика, 2000.
2.3 Лабораторная работа № 3 Определений характеристик одно- и многоканальных систем массового обслуживания.
1. Цель работы
Целью работы является ознакомление с методами определения характеристик простейших систем массового обслуживания (СМО) и получение навыков их использования.
2. Основные теоретические положения
Системы массового обслуживания с отказами.
СМО с отказами является такая система, в которой приходящие для обслуживания требования, в случае занятости всех каналов обслуживания, сразу ее покидают.
Вероятности состояний системы определяются из выражения
,
где
,
N – общее число каналов;
- нагрузка; -
интенсивность входящего потока
требований, -
интенсивность (производительность)
одного канала (прибора) обслуживания,
а вероятность отсутствия требований
определяется из выражения
.
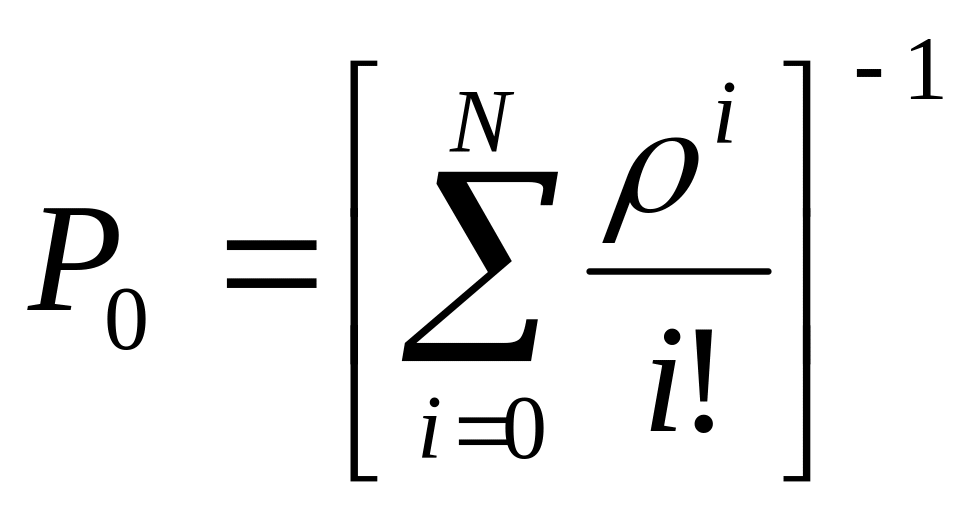К основным характеристикам качества обслуживания рассматриваемой СМО относятся:
Вероятность отказа
.
Среднее число занятых узлов обслуживания
.
Среднее число свободных узлов обслуживания
.
В системах с отказами события отказа и обслуживания составляют полную группу событий, отсюда
Относительная пропускная способность
определяется по формуле
.
Абсолютная пропускная способность СМО с отказами равняется
.
Коэффициент занятости узлов обслуживания определяется отношением средним числом занятых каналов к общему числу каналов
.
ПРИМЕР. В вычислительный центр коллективного пользования с тремя ЭВМ поступают заказы от предприятий на вычислительные работы. Если работают все три ЭВМ, то вновь поступающий заказ не принимается, и предприятие вынуждено обратиться в другой вычислительный центр. Пусть среднее время работы с одним заказом составляет 3 часа. Интенсивность потока заявок 0,25 ч-1. Найти вероятность отказа и среднее число занятых ЭВМ.
Имеем: m=3, =0,25
ч-1,
=3
ч. Находим:
,
,
,
.
Таким образом,
ЭВМ.
Системы массового обслуживания с ожиданием
СМО с ожиданием аналогична системе массового обслуживания с ограниченной длиной очереди при условии, что граница очереди отодвигается в бесконечность.
Вероятность состояний СМО с ожиданием находят по формулам:
,
для
,
,
для
.
При
в системе отсутствует стационарный
режим, при этом наблюдается явление
«взрыва» - неограниченный рост средней
длины очереди, поэтому для определения
должно выполняться ограничивающее
условие
,
и с учетом его запишем выражение:
.
В случае, когда стационарный режим в системе отсутствует, приведенные выше формулы теряют смысл и вычисление характеристик СМО по ним производить нельзя.
К основным характеристикам качества обслуживания СМО с ожиданием относят:
Вероятность наличия очереди Pоч, т.е. вероятность того, что число требований в системе больше числа каналов обслуживания:
.
Вероятность занятости всех каналов обслуживания в системе Pзан:
.
Среднее число требований в системе МТР:
.
Средняя длина очереди Mоч:
.
Среднее число свободных каналов обслуживания Мсв:
.
Среднее число занятых каналов обслуживания Мзан:
.
Коэффициент простоя K0 и коэффициент загрузки Kз каналов обслуживания системы:
;
.
Среднее время ожидания начала обслуживания Тож для требования, поступившего в систему:
.
Общее время, которое проводят в очереди все требования, поступившие в систему за единицу времени Тоож:
.
Среднее время Ттр, которое требование проводит в системе обслуживания:
.
Суммарное время, которое в среднем проводят в системе все требования, поступившие за единицу времени Тстр:
.
ПРИМЕР. В порту имеется два причала для разгрузки грузовых судов. Интенсивность потока судов равна 0,8 судов в сутки. Среднее время разгрузки одного судна составляет 2 сут. Предполагается, что очередь ожидающих разгрузки судов может быть неограниченной длины.
Найти среднее время пребывания судна в порту.
Имеем: m=2, =0,8
сут-1,
,
.
Находим:
;
;
.
Итак,
сут.
3. Порядок выполнения работы
3.1 Изучить теоретическую часть работы
3.2 Определить тип исследуемых систем массового обслуживания и их характеристики, используя таблицу 3.1 и задания 1 и 2.
3.3 С помощью пакета MathCad провести необходимые расчеты и построить графики.
3.4 Проанализировать полученные графики и сделать выводы по работе
3.5 Оформить отчет и сдать зачет по работе.
4. Практическая часть